网络流学习记录

序言

话痨出现！！
XC兴起安排了一天讲课，其中还有网络流，趁这个时间把网络流好好总结一下。
想让我在Blog里讲网络流原理？讲原理是不可能讲原理的，这辈子都不可能讲原理的。
网络流的算法多如浮云，就像麦趣鸡盒。（我才没有打广告）

听完课之后高兴的去研究国家历史。
推荐dalao的Blog。

---

前置技能

最大流问题的基本模型

P3376 【模板】网络最大流
通俗地讲，题面大概是这样子的：
现在给出一张有向图：

现在有若干个点的有向图，每个点的容量是无限的，其中点$S$有无限量的水，每条边有一个权值$w$，代表这条边的一次性流量为$w$个单位，询问最多可以有多少水流到点$T$。
显然，上图的最大流为$20$。

费用流问题的基本模型

P3381 【模板】最小费用最大流
通俗地讲，这个问题为最大流问题的加强版：每条边新增一个边权$c$，代表这条边的单位流量单价为$c$，在保证流量最大的同时使得费用最小/最大。

增广路

对于一条路径$(S,T)$，若其中所有边的残余流量都不为$0$，那么我们称其为一条增广路。
前置技能Get！！

最大流基本算法

基本操作（Ford-Fulkerson方法）

1. 找到一条增广路
2. 将增广路流完，同时添加反向弧

反向弧

我们可以看到，在基本操作中，有一个添加反向弧的操作。
对于一条搜索到的增广路中的每一条边$(u,v,w)$，在流完$w'$的流量后，添加一条$(v,u,w')$的反向边。
为什么要有添加反向弧这一个操作？
现在给出一个明显的例子：

显然，这张图的最大流是$2$。
但是，当经过这样一条增广路：


整张网络的流量就变为$1$了，显然，这是不正确的。
错误的原因就是我们没有给程序一个改正的机会。
那我们应该怎么做？回溯搜索显然是不行的。
既然如此，我们引入反向弧。
为什么添加反向弧就可以保证正确性？
再添加反向边后，我们就可以将之前流的流量给退回去，从而保证了其正确性。
这就是精华部分，利用反向边，使程序有了一个后悔和改正的机会。

Ford-Fulkerson

Ford-Fulkerson算法利用DFS实现搜索增广路，在搜寻到增广路后，更新网络。（其实就是暴力方法）
时间复杂度：$O(E|f^*|)$（$f^*$为最大流）
Ford-Fulkerson算法的缺点非常明显，因为其时间随着最大流增大而增大。若是在下面的这张图，Ford-Fulkerson算法可能会出现搜索时间过大的情况。

假如你运气不好，你可能会在中间的那条边一直跑。

Edmonds-Karp

Edmonds-Karp算法与Ford-Fulkerson算法最大的差异在于Edmonds-Karp算法利用BFS实现搜寻增广路，解决了由于最大流过大而引起的时间问题。
时间复杂度：$O(V^2E)$

Code

struct Edge
{
    int from, to , cap , flow;
    Edge(int u, int v, int c, int f) : from(u), to(v), cap(c), flow(f) {}
};

struct Edmonds_Karp
{
    int n, m;
    vector < Edge > edges;
    vector < int > G[MAXN];
    int a[MAXN];
    int p[MAXN];

    void init(int n)
    {
        for (int i = 0; i < n; ++i)
            G[i].clear();

        edges.clear();
    }

    void AddEdge(int from, int to, int cap)
    {
        edges.push_back(Edge(from, to, cap, 0));
        edges.push_back(Edge(to, from, 0, 0));
        m = edges.size();
        G[from].push_back(m - 2);
        G[to].push_back(m - 1);
    }

    int Maxflow(int s, int t)
    {
        int flow = 0;

        for (;;)
        {
            memset(a, 0, sizeof a);
            queue < int > Q;
            Q.push(s);
            a[s] = INF;

            while (!Q.empty())
            {
                int x = Q.front();
                Q.pop();

                for (int i = 0; i < G[x].size(); ++i)
                {
                    Edge &e = edges[G[x][i]];

                    if (!a[e.to] && e.cap > e.flow)
                    {
                        p[e.to] = G[x][i];
                        a[e.to] = min(a[x], e.cap - e.flow);
                        Q.push(e.to);
                    }
                }

                if (a[t])
                    break;
            }

            if (!a[t])
                break;

            for (int u = t; u != s; u = edges[p[u]].from)
            {
                edges[p[u]].flow += a[t];
                edges[p[u] ^ 1].flow -= a[t];
            }

            flow += a[t];
        }

        return flow;
    }
};

Dinic

Wiki:
Dinic算法与Edmonds–Karp算法的不同之处在于它每轮算法都选择最短的可行路径进行增广。Dinic算法中采用高度标号（level graph）以及阻塞流（blocking flow）实现其性能。

Kdmonds-Karp算法，每进行一次增广，都要做一遍BFS，十分浪费。能否少做几次BFS? 这就是Dinic算法要解决的问题。
简单来讲，Dinic算法通过BFS在参与网络上处理出距离标号，然后严格按照顺序进行增广。
每条在增广路中的边$(u,v)$必须严格满足$dep(u)=dep(v)+1$

意思就是说，下面这条增广路是不合法的。

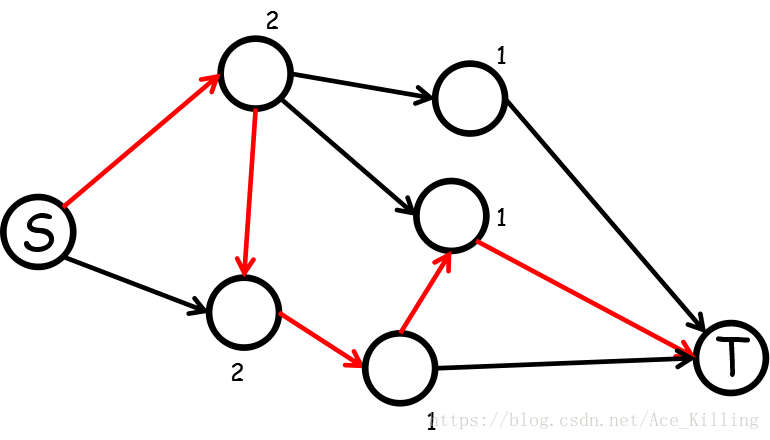
同时，在一次标号后，Dinic算法可以进行多路增广。（详见代码）
时间复杂度：$O(V^2E)$（二分图：$O(\sqrt{V}E)$）

Code

#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <queue>
using namespace std;

struct node
{
    int v, w, next;
    node() {}
    node(int _v, int _w, int _next) {v = _v, w = _w, next = _next;}
};

const int MaxN = 10000;
const int MaxM = 100000;

int n, m, s, t;
int ans;
node d[MaxM * 2 + 1];
int final[MaxN + 1], cnt = 1;//"cnt = 1"方便找到反向边
int cur[MaxN + 1]/*当前弧优化*/, dep[MaxN + 1]/*距离标号*/;

void Insert(int u, int v, int w)
{
    d[++cnt] = node(v, w, final[u]), final[u] = cnt;
}

bool Bfs()//处理距离标号
{
    memset(dep, 0, sizeof(dep));

    for (int i = 1; i <= n; i++)
        cur[i] = final[i];

    queue <int> q;
    q.push(s);

    for (; !q.empty(); q.pop())
    {
        int u = q.front(), v;
        dep[u]++;

        for (int i = final[u]; i; i = d[i].next)
            if (d[i].w && i % 2 == 0)
            {
                v = d[i].v;

                if (!dep[v])
                {
                    dep[v] = dep[u];
                    q.push(v);
                }
            }
    }

    return dep[t];
}

int Dfs(int u, int w)
{
    if (u == t)
        return w;

    int _w = 0;

    for (int i = cur[u]; i; i = d[i].next)
    {
        int v = d[i].v;
        cur[u] = i;//当前弧优化

        if (dep[u] + 1 == dep[v])//按照标号增广
        {
            int tmp = Dfs(v, min(w - _w, d[i].w));
            _w += tmp;
            d[i].w -= tmp;
            d[i ^ 1].w += tmp;
            //更新反向弧

            if (w == _w)
                return _w;
        }
    }

    return _w;
}

void Dinic(int u)
{
    for (; Bfs();)
        ans += Dfs(s, 1 << 30);
}

int main(int argc, char const *argv[])
{
    //freopen("init.in", "r", stdin);
    scanf("%d%d%d%d", &n, &m, &s, &t);

    for (int i = 1; i <= m; i++)
    {
        int u, v, w;
        scanf("%d%d%d", &u, &v, &w);
        Insert(u, v, w);
        Insert(v, u, 0);
        //添加正反向边
    }

    Dinic(s);
    printf("%d\n", ans);
    return 0;
}

ISAP

ISAP（Improved Shortest Augmenting Path）算法是另外一种基于分层思想的网络流算法，所不同的是，其节省了Dinic算法在每次增广后需要在残余网络上重新标号的问题，而是在每次增广完成后自动更新点的标号。（详见代码）
更重要的是，其引入了GAP优化，在下文会给予讲述。
时间复杂度：理论上为$O(V^2E)$，但在非二分图的情况下，由于GAP优化的引入，时间玄学。

Code

#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
using namespace std;

struct node
{
    int v, w, next;
    node() {}
    node(int _v, int _w, int _next) {v = _v, w = _w, next = _next;}
};

const int MaxN = 10000;
const int MaxM = 100000;

int n, m, s, t;
int ans;
node d[MaxM * 2 + 1];
int final[MaxN + 1], cnt = 1;
int cur[MaxN + 1];
int dep[MaxN + 1], st[MaxN + 1];

void Insert(int u, int v, int w)
{
    d[++cnt] = node(v, w, final[u]), final[u] = cnt;
}

int SAP(int u, int w)
{
    if (u == t)//流到汇点，退出
        return w;

    int _w = 0;

    for (int i = cur[u]; i; i = d[i].next)
    {
        int v = d[i].v;
        cur[u] = i;//当前弧优化

        if (d[i].w && dep[v] + 1 == dep[u])
        {
            int tmp = SAP(v, min(d[i].w, w - _w));
            _w += tmp, d[i].w -= tmp, d[i ^ 1].w += tmp;//更新反向弧

            if (w == _w)//满流退出
                return w;
        }
    }

    cur[u] = final[u];

    if (!(--st[dep[u]]))//重标号，GAP优化
        dep[s] = n;

    ++st[++dep[u]];//GAP优化
    return _w;
}

int main(int argc, char const *argv[])
{
    //freopen("init.in", "r", stdin);
    scanf("%d%d%d%d", &n, &m, &s, &t);

    for (int i = 1; i <= m; i++)
    {
        int u, v, w;
        scanf("%d%d%d", &u, &v, &w);
        Insert(u, v, w);
        Insert(v, u, 0);//添加反向弧
    }

    st[0] = n;

    for (; dep[s] < n;)//进行增广直至出现断层
        ans += SAP(s, 1 << 30);

    printf("%d\n", ans);
    return 0;
}

当前弧优化

在上文叙述的Dinic算法以及ISAP算法中都出现了数组$cur[]$——当前弧优化数组。
这是什么？为什么要这么做？
现在给出一个简单的问题：有一样事情在你的计划里，你已经完成的非常出色，现在叫你再去完成一遍，你愿意吗？
显然！！！没有人愿意。
同理，当前弧优化记录了当前走到的弧，避免了再次递归到时的重新枚举。

GAP（断层）优化

在ISAP算法中引入了GAP优化，即代码中的数组$st[]$。
$st[dep]$表示距离标号为$dep$的节点有$st[dep]$个。
有个十分显然的性质就是当其中的一个$st[]=0$时，网络出现断层，进而无法继续增广，算法结束。（详见ISAP算法代码）

费用流基本算法

对于费用流问题，我们依旧采用Ford-Fulkerson方法，采用Dinic算法，只不过将BFS标号改为SPFA或Dijkstar算最短路，每次沿着最短路增广。（但貌似多路增广会出锅，求dalao解释）

Code

#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <queue>
using namespace std;

struct node
{
    int v, w, dis, next;
    node() {}
    node(int _v, int _w, int _dis, int _next) {v = _v, w = _w, dis = _dis, next = _next;}
};

const int MaxN = 5000;
const int MaxM = 50000;

int n, m, s, t;
int ans, cost;
node d[MaxM * 2 + 10];
int final[MaxN + 1], cnt = 1;
int cur[MaxN + 1], dis[MaxN + 1];
int _w[MaxN + 1], prev[MaxN + 1];
bool bj[MaxN + 1];
queue <int> q;

void Insert(int u, int v, int w, int dis)
{
    d[++cnt] = node(v, w, dis, final[u]), final[u] = cnt;
}

bool SPFA(int s, int t)
{
    memset(dis, 0x7f, sizeof(dis));
    memset(_w, 0x7f, sizeof(_w));
    memset(bj, false, sizeof(bj));
    bj[s] = true;
    dis[s] = 0;
    prev[t] = 0;
    q.push(s);

    for (; !q.empty(); q.pop())
    {
        int u = q.front(), v;

        for (int i = final[u]; i; i = d[i].next)
        {
            v = d[i].v;

            if (d[i].w && dis[v] > dis[u] + d[i].dis)
            {
                dis[v] = dis[u] + d[i].dis;
                prev[v] = u;
                cur[v] = i;
                _w[v] = min(_w[u], d[i].w);

                if (!bj[v])
                {
                    q.push(v);
                    bj[v] = true;
                }
            }
        }

        bj[u] = false;
    }

    return prev[t];
}

void Mininum_Cost_Maxinum_Flow()
{
    for (; SPFA(s, t);)
    {
        int u = t;
        ans += _w[t];
        cost += _w[t] * dis[t];

        while (u != s)
        {
            d[cur[u]].w -= _w[t];
            d[cur[u] ^ 1].w += _w[t];
            u = prev[u];
        }
    }
}

int main(int argc, char const *argv[])
{
    freopen("init.in", "r", stdin);
    scanf("%d%d%d%d", &n, &m, &s, &t);

    for (int i = 1; i <= m; i++)
    {
        int u, v, w, dis;
        scanf("%d%d%d%d", &u, &v, &w, &dis);
        Insert(u, v, w, dis);
        Insert(v, u, 0, -dis);
    }

    Mininum_Cost_Maxinum_Flow();
    printf("%d %d\n", ans, cost);
    return 0;
}

总结

话痨出现！！
对的没有错，我又来说垃圾话了。
网络流这种1956年的巨佬提出来的东西，现在变成了OI毒瘤……
怎么讲，网络流这个东西如果裸的出现，那么它一般是预流推进了，你可以准备上暴力。
但如果它出现在题里，要你建模的话，恭喜你，你是不可能建出模型的，你可以准备上暴力。（除非你是dalao，蒟蒻在此膜拜）