再探马周游问题

【转载】买回了王晓东的《算法设计与分析习题解答》，书中代码是用Java写的，看了跳马问题的部分，基本理解了算法。首先说明一下，《算法设计与分析》原书的题目其实是要找一条哈密尔顿通路，而《习题解答》中是解哈密尔顿回路的，即不仅要不重复的跳过棋盘的每一个格子，最后还要能回到出发点。先解释一下寻找哈密尔顿回路的算法：
【问题描述】
对于给定的m × n的国际象棋棋盘，m和n均为大于5的偶数，且|m - n| <= 2，试设计一个分治算法找出一条马的哈密尔顿回路。
【算法】
首先，考虑n × n的棋盘，马踏棋盘是黑白相间的，对于一条哈密尔顿回路来说，马在棋盘上所踏过的黑色格子和白色格子相等，因此，棋盘的格子数应为偶数，n不能为奇数。即n为奇数的n × n棋盘不存在哈密尔顿回路（但可能存在哈密尔顿通路）。而对于m × n的棋盘（m != n），m, n均为奇数则不存在哈密尔顿回路。好在题目已经限定m, n均为偶数且|m - n| <= 2，这说明在这种情况下一定存在哈密尔顿回路。而在其他情况下，如m, n一奇一偶或|m - n| > 2是否存在哈密尔顿回路则不好说。至于题目为何要做此限定，如何证明这种限定的合理性则有待探究，当然对此问题的讨论也超过了本文的范围。
现在回到题目本身，算法考察一类具有特殊结构的解，这类解在棋盘的4个角都包含2条特殊边，如下图。称具有这类特殊结构的哈密尔顿回路为结构化的哈密尔顿回路。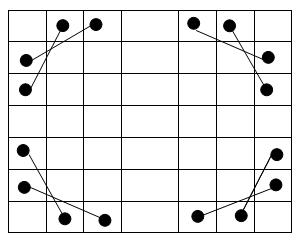

用回溯法可在O(1)（留有疑问）时间内找出6 × 6, 6 × 8, 8 × 8, 8 × 10, 10 × 10, 10 × 12棋盘上的结构化的哈密尔顿回路。同时注意到四个角上每个点只有两条边，而哈密尔顿回路要经过这个角，走的边不能重复，因此这两条边必然在汉密尔顿回路的路径上。故结构化的解一定形如下图：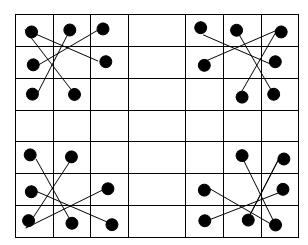

而对于6 × 8, 8 × 10, 10 × 12的棋盘，旋转90度即可得到8 × 6, 10 × 8, 12 × 10的棋盘上结构化的哈密尔顿回路。
对于m, n >= 12的情形，采用分治策略。
1. 分治：将棋盘尽可能的平均分割成4块，当m, n = 4k时，分割为2个2k；当m, n = 4k + 2时，分割为1个2k和1个2k + 2。
2. 合并：4个子棋盘拼接后如下图：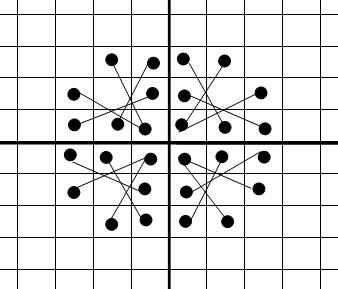



分别删除4个子棋盘中的结构化的边A, B, C, D，添入新的边E, F, G, H，构成整个棋盘结构化的哈密尔顿回路，如下图所示：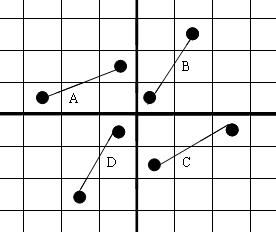
                
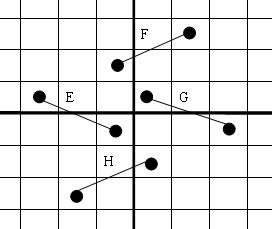
从图中可以看出， 合并的过程其实很简单，如果把A, D, C, B看作风扇的桨叶，则合并后就是将桨叶依次逆时针向下打了一个点（逆时针旋转）。
至此，算法结束，我们可以看到，当n >= 12是使用分治法，分成4个子棋盘，而合并过程只需常数时间即可完成，设该算法时间为T(n)，则有递推方程：T(n) = 4T(n / 2) + O(1)，据Master定理知T(n) = O(n ^ 2)，这就是在棋盘中寻找哈密尔顿回路的时间复杂度。比《跳马问题（骑士周游问题）初探 》一文中从给定起始点寻找哈密尔顿通路的问题快了不少。
【分析】
回到《算法分析与设计》一书中课后的那道题，是否存在一个分治的求哈密尔顿通路的算法呢？这个问题我现在还没有确切的答案，因为从网上搜索的一些资料看（CSDN的帖子中很多人问了这个问题），有几个网友说有一篇论文似乎是论述了类似的问题，分治的方法十分复杂，要根据不同的情况去分割问题，但很遗憾，这些网友们给出的论文地址已经无效，我没有看到确切的方法。
但如果想用类似解哈密尔顿回路的算法来解决哈密尔顿通路的问题，我分析认为不可能（即要分治不可能是像解回路一样分治，如前所说，答案可能在那篇神秘的论文中）。这种不可能正是由于“回路”和“通路”这一字之差引起的：回路与起始点无关，算法只需在棋盘中能够找到一条哈密尔顿回路，则从任何一点都能不重复的经过棋盘上每一点并回到起始点。而哈密尔顿通路与起始点有关，且路径不是封闭的，这就使得回路中考察的结构化路径的解可能不存在，考虑起始点在最左上角的情形，通路不用再回到这个左上角，所以角上的两条边只用一条，这样在合并时通路问题就不会出现结构化路径中的中心对称结构。 因此，我们不能从回路算法中得到启发去找到通路问题的分治解。
当然，由于通路是比回路弱的一个解要求，当棋盘满足m, n为偶数，m, n >= 6且|m - n| <= 2的条件时，我们可以直接调用这个回路算法得到一条哈密尔顿回路，然后删去起始点和终点的边即得通路的解，而在不满足这个条件时，如5 × 5的棋盘上，对某些起始点是存在哈密尔顿通路的，仍然需要使用回溯的算法去求解，时间复杂度为O(8 ^ (m * n))。
从回溯算法的时间复杂度，又引出前面书中所说：“用回溯法可在O(1)时间内找出6 × 6, 6 × 8, 8 × 8, 8 × 10, 10 × 10, 10 × 12棋盘上的结构化的哈密尔顿回路。”的疑问，回溯法怎么可能是在O(1)时间内得到这些棋盘上回路的解呢？如果这样，就要求在这些规模的棋盘上构建议一条结构化的回路（即四角对称的回路）有固定的跳马方法，这种方法使得每一步跳马时的步子只有唯一选择，但即使这样也至少是个线性时间的复杂度啊。从书中的源代码看，好像是直接一一的读取这些规模棋盘上的回路（即回路已经手工构造好了），这样复杂度才是O(1)，所以书中的这句话应该有错。
另外需要说明的是书的所附光盘并没有源代码，只有几个testcase，十分的遗憾（不知为什么不放，可能是怕盗版，大家拿到源码后都不买书了吧:)，不过这一点比之国外教材就差了）。而书中的源代码中ReadStream在Java API中并不存在，kyeboard.readInt()也不知是从哪读的数据（光盘上也没有），反正代码中是用这个类来初始化6 × 6, 6 × 8, 8 × 8, 8 × 10, 10 × 10, 10 × 12这些特殊规模棋盘的解的。这种缺憾使得源码不能上机跑起来，我也没有手工的跑这个程序去分析（有时间再说吧），另外书中的代码的注释实在是太少了。这些遗憾都使得该书对读者来说不太方便。
【参考文献】
[1] 《计算机算法设计与分析（第2版）》 王晓东 电子工业出版社
[2] 《算法设计与分析习题解答》 王晓东 清华大学出版社