《C算法》读书笔记 （4）：Hello，Joseph！

P67, 3-8 约瑟夫问题

上一篇文章中提到了使用链表模拟约瑟夫问题求解。约瑟夫问题是这样的 ：假设有N个人决定选出一名领导，将所有人排成一个圆周，从1编号到N。现在从1开始，数M个人，最后的M出列。重复上述步骤，直到只剩下一个人，该人即为领导。
首先定义链表的数据结构：

typedef struct node *link;
struct node 
{
    int item;
    link next;
};

将node称为节点。现要删除节点p->next，只需要使p->next=p->next->next。

void sim_joseph()       // 链表模拟
{
    link p, t;
    t = p = (link)malloc(sizeof(node)), p->item = 1, p->next = p;
    for(int i = 2; i <= n; ++ i)
    {
        p = (p->next = (link)malloc(sizeof(node)));
        p->item = i;
    }
    p->next = t;

    for(int i = 0; i < n - 1; ++ i)     // n - 1 times execute
    {
        for(int j = 0; j < m - 1; ++ j)
            p = p->next;
        //printf("%d is killed\n", p->next->item);
        t = p->next;
        p->next = p->next->next;
        free(t);
    }
    printf("%d remains alive\n", p->item);
    free(p);
}

---

显然，该算法的复杂度为$O(N*M)$
有没有更好的算法？答案是肯定的。
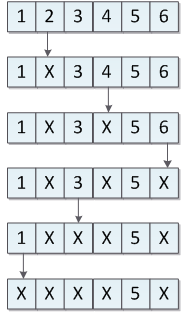
假设有一个N=6，M=2的样例，也就是6个人围成一圈，每次报2个数，直到最后一个人。
样例的流程如下：

为了便于理解，我们将N=6，5，4时的最后一个人先利用链表法计算出来：
N=5，M=2时，最后的结果为3，记$F(5,2)=3$
同理得，$F(4,2)=1$，$F(6,2)=5$
将所有编号减1（为了计算的简便性，此时$F(5,2)=2$，$F(6,2)=4$），分析第一步：

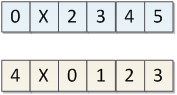
在1号选手被淘汰出局后，剩下的五人实际上重新组成了一个新的约瑟夫问题$F(5,2)$，唯一的区别就是，新一局的选手0在上一局里面编号为2，选手1在上一局编号为3，以此类推。可以建立一个映射关系：

$$H(x) = \bigg(\widetilde H(x)+M\bigg)\bmod N$$
其中 $\widetilde H(x)$代表新一局里面的编号， $N$为当前问题人数

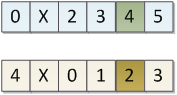
易见，在5人问题中最后的胜者2，在6人问题中编号为4。
同理，在4人问题中最后的胜者1，在5人问题中编号为3。

如此递推，存在边界：1人问题最后胜者为0。从1人问题依次反推就得到解。
该算法的复杂度为$O(N)$

完整的程序如下：

#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <algorithm>
using namespace std;

typedef struct node *link;
struct node 
{
    int item;
    link next;
};
int n, m;

void linear_joseph()    // 递推
{
    int ans = 0;
    for(int i = 2; i <= n; ++ i)
    {
        ans = (ans + m) % i;
    }
    printf("linear shows %d remains alive\n", ans + 1);
}

void sim_joseph()       // 链表模拟
{
    link p, t;
    t = p = (link)malloc(sizeof(node)), p->item = 1, p->next = p;
    for(int i = 2; i <= n; ++ i)
    {
        p = (p->next = (link)malloc(sizeof(node)));
        p->item = i;
    }
    p->next = t;

    for(int i = 0; i < n - 1; ++ i)     // n - 1 times execute
    {
        for(int j = 0; j < m - 1; ++ j)
            p = p->next;
        //printf("%d is killed\n", p->next->item);
        t = p->next;
        p->next = p->next->next;
        free(t);
    }
    printf("sim shows %d remains alive\n", p->item);
    free(p);
}

int main()
{
    freopen("in.txt", "r", stdin);
    freopen("out.txt", "w", stdout);

    while(scanf("%d%d", &n, &m) != EOF)
    {
        sim_joseph();
        linear_joseph();
    }

    return 0;
}