二叉树,完全二叉树,满二叉树,完美二叉树（有图干货）

 二叉树：树中每个节点至多有两个子节点

【最普通的二叉】

二叉搜索树：对于树中任何节点，如果其左子节点不为空，那么该节点的value值永远 >= 其左子节点；如果其右子节点不为空，那么该节点的value值永远 <= 其右子节点

【回顾一下中序遍历】

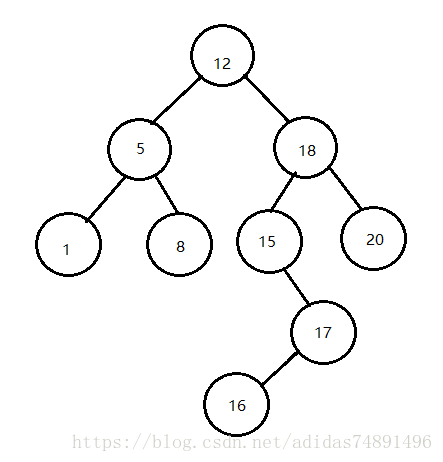
满二叉树（Full Binary Tree）：树中除了叶子节点，每个节点都有两个子节点

美国NIST给出的定义为：

A binary tree in which each node has exactly zero or two children.

In other words, every node is either a leaf or has two children.

For efficiency, any Huffman coding is a full binary tree.

满二叉树的任意节点，要么度为0，要么度为2.换个说法即要么为叶子结点，要么同时具有左右孩子。霍夫曼树是符合这种定义的，满足国际上定义的满二叉树，但不满足国内的定义。

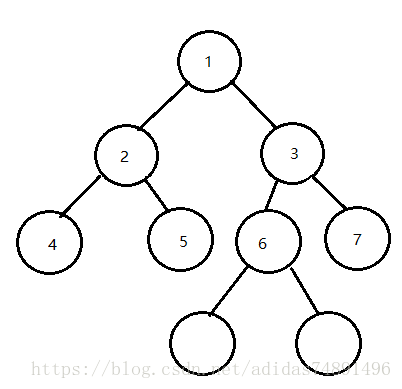
国内定义：一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。

也就是说，如果一个二叉树的层数为K，且结点总数是(2^k) -1 ，则它就是满二叉树。

完全二叉树（Complete Binary Tree）：在满足满二叉树的性质后，最后一层的叶子节点均需在最左边

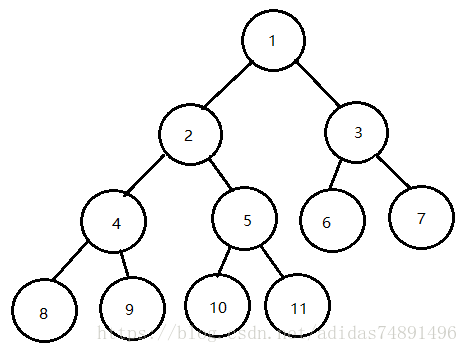
完美二叉树（Perfect Binary Tree）：满足完全二叉树性质，树的叶子节点均在最后一层（也就是形成了一个完美的三角形）

任何一个完美二叉树 既属于满二叉树，也属于完全二叉树。因此它拥有满二叉树和完全二叉树的所有性质

完美二叉树从外观上看他是一个等边三角形。他的每一层都被填充满。

【自行脑补】

满二叉树、完全二叉树、完美二叉树的定义是越来越严格的

哈夫曼树

哈夫曼树（Huffman Tree）是在叶子结点和权重确定的情况下，带权路径长度最小的二叉树，也被称为最优二叉树

建议查看以下链接，生动易懂

百度安全验证