1.SVM相关知识
首先我们知道线性SVM是这样一个分类器,它寻找具有最大边缘的超平面。考虑一个包含N个训练样本的二元分类问题,类标签为-1或者1。 SVM分类器的决策边界为:

即为下图虚线所示:
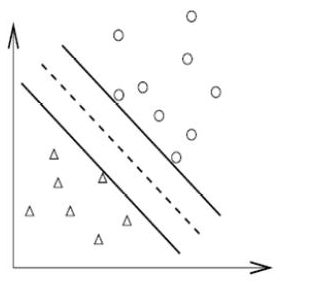
其中w的方向与虚线垂直(可证明)。通过调整决策边界的参数w和b,得到两个超平面。
其中在虚线上方且与虚线平行的超平面L1为:
其中在虚线下方且与虚线平行的超平面L2为:
w*x+b=-1
令x1是L1上的一个数据点,令x2是L2上的一个数据点,将x1和x2代入以上公式中,则有:
两式相减可得:
其中d为超平面L1与超平面L2之间的直线距离。 我们的目标是使得d最小。
2.学习线性SVM模型
SVM的训练阶段即从训练数据中估计参数w跟b。选择的参数必须满足:

即类标签为1的训练实例都必须位于超平面L1上或者位于它的上方,而那些类标签为-1的训练实例必须位于超平面L2上或者L2的下方。
对上述两个不等式可概括为:
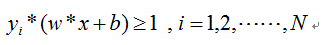
我们的目标是最大化d,即最小化||w||,等价于最小化下面的目标函数:
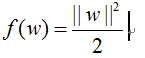
那么SVM的任务即可以描述为如下优化问题:








 本文介绍了支持向量机(SVM)的基本概念,特别是线性SVM寻找最大边缘的超平面。在二元分类问题中,SVM的目标是找到使间隔最大的超平面。通过拉格朗日乘子法,将原始优化问题转化为对偶问题,最终求解SVM的参数w和b。文章还展示了SVM的简单代码实现。
本文介绍了支持向量机(SVM)的基本概念,特别是线性SVM寻找最大边缘的超平面。在二元分类问题中,SVM的目标是找到使间隔最大的超平面。通过拉格朗日乘子法,将原始优化问题转化为对偶问题,最终求解SVM的参数w和b。文章还展示了SVM的简单代码实现。
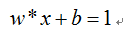
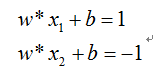
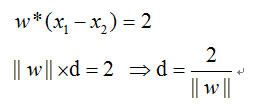
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 1926
1926

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








