SFGAE: a self-feature-based graph autoencoder model for miRNA–disease associations prediction


目录
Step 1: construct feature representations
Step 2: construct self-feature embeddings
Step 3: construct aggregated feature embeddings
Step 3.1: construct primitive aggregated feature embeddings.
Step 3.2: construct aggregated self-feature embeddings.
Step 3.3: combine under attention mechanism.
Parameter setups and evaluation metrics
Effect of semantic similarities
Effect of self-feature embeddings
Effect of training sample sizes
Effect of imbalance of dataset
Effect of the number of encoder layers
Effect of embedding dimensions
Performance of SFGAE on HMDD v3.2
Abstract

越来越多的证据表明,microRNAs(miRNAs)是各种疾病的重要生物标志物。 许多图神经网络(GNN)模型已经被提出来预测miRNA - 疾病的联系。 然而,现有的基于GNN的方法都存在过平滑问题--在多个GNN层堆叠时,学习到的 miRNA 节点和疾病节点的特征嵌入难以区分。 该问题使得方法的性能对层数很敏感,当使用更多层时,性能会受到显著影响。 在本研究中,我们通过一个新的基于自特征的图形自动编码器(self-feature-based graph autoencoder)模型来解决这个问题,简称为SFGAE。 SFGAE的主要创新之处在于构造了miRNA自嵌入 (miRNA-self embeddings) 和疾病自嵌入 (disease-self embeddings) ,并使它们独立于两类结点之间的图交互。 新的自特征嵌入丰富了典型的聚集特征嵌入的信息,这些聚集特征嵌入聚集了来自直接邻居的信息,因此严重依赖于图的交互。 SFGAE采用带注意力机制的图编码器将聚集特征嵌入和自特征嵌入串联起来,采用双线性译码器预测链接。 我们的实验表明SFGAE达到了最先进的性能。 特别地,SFGAE在基准数据集 HMDD V2.0 和 HMDD V3.2 上改进了最近GAEMDA[1]上的平均AUC,并且在使用较少(例如10%)训练样本时始终表现得更好。 此外,SFGAE有效地克服了过平滑问题,并在更深的模型(如八层模型)上表现稳定。 最后,我们对三种人类疾病,结肠肿瘤、食管癌和肾肿瘤进行了个案研究,并以肾肿瘤为例进行了生存分析。 结果表明,SFGAE是预测潜在的miRNA - 疾病关联的可靠工具。
关键词:miRNA与疾病关联预测,图形自动编码器,自特征嵌入,注意力机制
Introduction

MicroRNAs(miRNAs)是一类含有约22个核苷酸的单链非编码RNAs。 近十年来,研究者一直致力于研究miRNAs的表达谱,并为miRNAs在各种疾病中的表达变化提供了坚实的证据。 如[2,3]表明miR-375、miR-125b-5p和miR-5190的异常表达可导致1型和/或2型糖尿病。 [4,5]和[6,7]还分别发现了某些miRNAs在神经系统疾病、心脏病和癌症中的表达变化。 我们参考文献[8],文献对miRNAs在人类疾病中的功能进行了简要的调查。 鉴于miRNAs是多种疾病发生和发展的重要生物标志物,确定它们之间的潜在联系具有重要的现实意义。


有大量文献通过实验或计算方法探索 miRNA 与疾病的关联。实验方法直接、明确;因此,他们确定的关联是可靠的,并且在很大程度上被医学界所接受。基于实验验证的结果,研究人员建立了多个生物信息学基准数据库。例如,miRTarBase [9]、PmiRtarbase [10] 和 miRDB [11] 是流行的 miRNA - target相互作用数据库;和 miR2Disease [12]、dbDEMC [13] 和 HMDD [14] 是流行的 miRNA-疾病关联数据库。实验方法的主要技术包括引物延伸(primer extension)和微阵列分析(microarray profiling)等。参见[15-17]及其中的参考文献。然而,实验方法有两个紧迫的局限性。首先,它们在时间、劳动力和金钱方面的成本很高。 目前只有数百种 miRNA 得到定量验证,与2500多种人类 miRNA 相比,这是有限的[18]。其次,传统实验假设的“一个 miRNA - 一个靶基因 - 一种疾病”的相关机制缺乏对人类系统的全局观,使实验效率低下。为了解决这个问题,计算机科学家也提出了不同的计算方法。

计算方法通常是更经济、更有效的关联预测方法。 计算方法可以为每种疾病返回排名靠前的预测miRNAs,并帮助研究人员进一步设计生物学实验来相应地验证这些miRNAs。 现有的计算方法可以分为三类:基于相似度的方法、基于机器学习的方法和基于图的方法。 我们简要回顾每一个类别如下,并指出读者去阅读[19]近期全面的综述。 我们还介绍了所提出的基于图的方法SFGAE如何解决现有的局限性。



基于相似度的方法。 基于相似度的方法依赖于这样一个假设,即功能相似的miRNAs往往与具有相似表型的疾病相关[20]。 特别的miRNA-miRNA相似性包括功能相似性(functional similarity)[21]、表达相似性(expression similarity)[22]、序列相似性(sequence similarity)[23]和生理相似性(physiological similarity)[24]; 疾病-疾病相似性包括语义相似性(semantic similarity)[25]和本体相似性(ontological similarity)[26]。 基于上述相似性,人们提出了许多关联预测方法。 例如,[27]用高维向量来表示miRNAs的表达相似度和疾病的语义相似度,并通过计算向量空间中的向量相似度来预测关联。 [28]用Levenshtein距离度量的功能相似性代替表达相似性,并用阳性样本预测关联。 [29]设计了一种相似核融合算法来集成相似矩阵,并将拉普拉斯正则化方法应用于链接预测。 [30]基于局部约束线性编码方法集成相似性矩阵,并在集成矩阵上应用标记传播策略进行链接预测。尽管基于相似度的方法在效率方面优于实验方法,其预测的关联大多得到了实验验证,但这类方法只关注miRNA和/或疾病中不同类型的相似性,而忽略了每个miRNA和疾病的个体性和唯一性。 事实上,正如后面所看到的,其他两种类型的方法也有这种限制。 虽然研究miRNAs与疾病的相似性是很有动机的(因为相似的miRNAs应该与相似的疾病联系在一起),但作为本文的主要贡献,我们表明适当地考虑每个miRNAs和疾病的独特性可以使相似性度量更加精确,并显著地提高预测的准确性。


基于机器学习的方法。研究人员已将各种机器学习方法应用于 miRNA - 疾病关联的预测,这些方法主要涵盖随机游走( random walks )、支持向量机 ( support vector machines )(SVMs)、k 最近邻 ( k-nearest neighbors )(k-NNs) 和决策树( decision tree )。
特别地,[31]将随机游走算法应用于两层miRNA-疾病相似度网络,其转移概率与功能或语义相似度成正比,依赖于节点的类型。 [32]训练了一个SVM分类器来分离阳性的关联和阴性的关联。 [33]寻找miRNAs和疾病的k个最近邻,并在K-NN算法上建立排序模型,以获得所有可能关联的最终排序。 [34]用梯度上升法(gradient boosting)训练决策树模型 。每次树分裂(tree split)都是减少总的回归损失的优化操作,使用已完成的树进行预测。[35] 为每个miRNA和疾病对构建评级,并实现了两分网络推荐算法用于预测。 [36]引入了miRNA序列信息和自然语言处理技术提取的特征。 [37]通过基于k-means的正和负样本进行随机采样,提出了一种自适应性增强(adaptive boosting)方法,从而实现更高的效率和可扩展性。 [38]提出了一种新型模型,通过增强贝叶斯个性化排名,可以利用未知样本,而不是将其视为阴性样本。 [39]为新特征向量构建了深度信念网络和预训练的限制Boltzmann机器。 随后,[40]设计了一个堆叠的自动编码器模型,以无监督的方式预先训练它,并以监督的方式微调它。 此外,[41]基于随机森林算法提出的预测方法;[42-45]基于矩阵完成算法提出的预测方法。 这两种类型方法都应用于其他问题[46,47],并在简单的设置下进行分析[48,49]。 然而,现有的基于机器学习的预测方法仍然忽略了每个miRNA和疾病的独特性。


基于图的方法。miRNA-disease 数据结构自然地归纳出一个二分图:所有的miRNA节点都在一个类中; 所有disease节点都在另一类; 来自两不同类的两个节点之间的联系提示这种miRNA与该disease有关。 这样的二分图拓扑使图论得以应用[50,51],并使基于图神经网络(GNN)的各种应用的方法于关联预测成为可能,例如图卷积网络(GCNs)[52,53]和图注意力网络(GATs)[54]。 最近,[55]提出了一个层注意力GCN(LAGCN)模型,将药物-药物、疾病-疾病相似性和药物-疾病关联集成到一个单一的异构图中,并基于图卷积运算得到的节点嵌入预测关联。 虽然[55]研究了药物与疾病的关联,但该方法也适用于miRNA与疾病的关联。 [56]提出了一种多通道注意力GCN模型,利用GCN获取miRNAs和疾病的特征,并通过注意力神经网络对特征赋予不同的权重后再进行预测。 另外,[57]结合矩阵分解和异构图推理的优点,建立了关联预测模型。 [58]用变分自动编码器设计了一个无监督深度学习框架。 作为相关的工作,[1]提出了一个称为GAEMDA的图自编码器模型。 GAEMDA在编码器阶段采用两个GNN层来聚合直接邻居的信息,得到每个节点的低维嵌入; 该算法还采用了双线性译码器进行关联预测。 与流行的基线 (baseline) 方法相比,作者在实验中表明,GAEMDA具有最先进的性能。 然而,[1]也承认,由于GNNs的过平滑问题,所提出的编码器模型很难扩展到很深的层次。当然,一方面,增加GNNs的深度可以更好地挖掘和解释复杂的miRNA疾病数据集的信息。 另一方面,堆叠更多的层导致与邻居的更多交互,最终使得不同(类型)节点的学习嵌入相似。 因此,与前面介绍的其他两类方法一样,现有的基于图的方法由于图上有许多直接邻居的聚集,使得每个节点的唯一性被平滑掉。


为了克服过度平滑的瓶颈,并让每个节点保持其唯一性,我们决心增加 GNN 模型的宽度。特别地,我们提出了一种基于GNN的方法,称为基于自特征的图形自动编码器模型,简称为SFGAE。 SFGAE的主要创新之处在于它构造了miRNA自特征嵌入和disease自特征嵌入,并提供了一种将这些新的自特征嵌入到GNN模型中的方法。 特别地,我们以一种非常简单的方式获得自特征嵌入,只需通过全连通网络(FCNs)。 然后,我们利用注意力机制来实现(典型的)聚集特征嵌入与新的自特征嵌入。 后者极大地丰富了前者的信息,从而增加了模型的宽度。我们强调聚合特征嵌入是通过聚合邻居信息(使用一定的聚合函数)来获得的。 由于二分图的结构,miRNA的邻居是disease,disease的邻居是MIRNA。 因此,当执行越来越多的聚合时,学习到的节点嵌入越来越相似(即过平滑问题)(over-smoothing)。 然而,构造的自特征嵌入独立于图的交互,因此这些嵌入不会与任何邻居的嵌入混合。 因此,自特征嵌入保留了每个节点的唯一性。 总体而言,SFGAE的编码步骤包含自特征嵌入(来自FCNs)的构造和聚合特征嵌入(来自聚合函数)的构造,而与[1]类似,关联预测采用双线性译码器。



我们在被广泛使用的基准数据集HMDD V2.0和HMDD V3.2上进行了大量的实验,评估了SFGAE的性能。 我们主要说明了在HMDD V2.0上的性能,因为[1]中的参考模型GAEMDA是在V2.0上实现的。 然而,我们使用HMDD V3.2数据集来验证我们的模型的优点也适用于其他数据集。 首先,我们对模型中的关键组件进行了有效性测试,包括所采用的FCNs和注意力机制,结果表明所有组件都是有效的,能够提高模型的性能。 特别地,一个FCN层足以显著增强性能。 其次,对SFGAE和GAEMDA在不同数据层次上进行了比较。 我们改变训练集占整个数据集的比例从1/10到1/2,并表明SFGAE在每个层次上都优于GAEMDA。这一结果说明了SFGAE是样本有效的(sample efficiency)。第三,在不平衡数据集上测试了SFGAE的性能。 我们从{1/2,1/6,1/10}中改变正样本与负样本的比例,我们观察到SFGAE比GAEMDA稳定地表现得更好(尽管差异不像平衡数据集上的差异那么显著,但我们认为处理不平衡需要一个 ad hoc 模型设计;在这个意义上,建议的参考模型(和SFGAE)的适用性有限)。 第四,我们测试了隐藏GNN层数的影响,我们观察到当GNN深至8层时,SFGAE仍然表现稳定,而GAEMDA表现不佳。 这一观察结果与文献[1]的预期一致,并说明我们的自特征嵌入技术有效地克服了过平滑问题。 第五,与现有的其它方法进行了比较,结果表明SFGAE达到了最优性能,并且对其它方法有明显的改进。 例如,通过5折交叉验证,我们将GAEMDA曲线下的平均面积从93.56%提高到94.19%。 最后,我们对三种与肿瘤有关的人类疾病进行了个案研究,并以肾脏肿瘤为例进行了生存分析。我们观察到,对于每一种疾病,SFGAE预测的前40个miRNAs几乎都被最近的生物学研究证实了。 此外,前40位 miRNA 候选者中有18位具有统计学意义,P 值 < 0.05。这一观察结果说明了我们的SFGAE模型的可靠性。 我们的实现代码可在以下网址获得GitHub - AI-luyuan/SFGAEContribute to AI-luyuan/SFGAE development by creating an account on GitHub. https://github.com/AI-luyuan/SFGAE
https://github.com/AI-luyuan/SFGAE
Methods

在本节中我们介绍了SFGAE模型。 该模型由四个步骤组成; 第一步是特征构建; 第二和第三步骤为编码器步骤; 第四步是解码器步骤。 该模型的核心是自特征嵌入的构造(第二步)和自特征嵌入与(典型的)聚集特征嵌入的结合(第三步)。 后一种嵌入是由[1]提出的,本文将其命名为原始聚集特征嵌入。
为了对模型有一个全局的感觉,我们首先给出一个模型草图,然后介绍每个步骤的细节。
SFGAE草图 :如前所述,miRNA与疾病关联的数据自然形成一个二分图。 在这个图上,所有的miRNA节点都在一个类中; 所有疾病节点都在另一类; 通过关联得到两类结点之间的边。 基于这样的图,SFGAE由四个步骤组成,如图1所示:特征构造、自特征嵌入构造![]() ,精炼聚合特征嵌入构造
,精炼聚合特征嵌入构造![]() 和关联预测。
和关联预测。


特别地,在第一步中,我们结合miRNAs的功能相似度、疾病的语义相似度以及疾病与miRNAs的高斯互作谱核相似度,为每个节点构造原始的特征表示。 此步骤基于开源数据集,类似的特征构造步骤在以前的工作中被采用[1,59,60]。 在第二步中,我们首先对特征表示应用仿射变换来匹配miRNAs和疾病的特征维数。 然后,我们将FCNs应用于特征表示,得到自特征嵌入。 随着模型的深入,通过简单地组合更多的FCN操作来更新自特征嵌入(参见(1))。 我们在实验中测试了层数对FCN操作的影响,并观察到单层足以获得有希望的性能。 在第三步中,我们应用注意力机制来获得精炼的聚集特征嵌入。 注意力层的输入是原始聚集特征嵌入和聚集自特征嵌入,这两种嵌入都是通过对每个节点的邻居应用一定的聚集函数得到的。 注意力层的输出是精炼的聚集特征嵌入(参见(3)和(4))。 通过引入注意力机制,我们的自特征嵌入丰富了原始聚集特征嵌入的信息。 第四步,我们采用一个标准的双线性译码器来预测miRNA节点和疾病节点之间的潜在联系。
Step 1: construct feature representations

设G= (M , D , E)为miRNA-疾病二部图,其中![]() 为 miRNA 集,其中
为 miRNA 集,其中![]() 为 miRNA 的数目;
为 miRNA 的数目; ![]() 是疾病节点的集合,其中
是疾病节点的集合,其中![]() 是疾病的个数; 而
是疾病的个数; 而![]() 是边集。 在这一步中,我们为每个miRNA节点
是边集。 在这一步中,我们为每个miRNA节点![]() 和每个疾病节点
和每个疾病节点![]() 提供了一个特征表示。 我们综合了三个相似性:miRNA功能相似性、疾病语义相似性和 miRNA-疾病高斯互作谱核相似性。
提供了一个特征表示。 我们综合了三个相似性:miRNA功能相似性、疾病语义相似性和 miRNA-疾病高斯互作谱核相似性。

1 MISIM is available at https://www.cuilab.cn/files/images/cuilab.
miRNA功能相似性由[21]提供。 总结在公共数据库![]() 中,我们可以得到一个功能相似矩阵
中,我们可以得到一个功能相似矩阵![]() ,它是一个条目在0~1之间的对称矩阵。 条目越大,两个 miRNAs 越相似。 注意,我们故意用
,它是一个条目在0~1之间的对称矩阵。 条目越大,两个 miRNAs 越相似。 注意,我们故意用![]() 来区分
来区分![]() ,前者是 MISIM 中 miRNAs 的数目,而后者是图上 miRNAs 的数目。 在我们的研究中,我们基于miRNA-疾病关联数据库HMDD构建了二部图,我们有
,前者是 MISIM 中 miRNAs 的数目,而后者是图上 miRNAs 的数目。 在我们的研究中,我们基于miRNA-疾病关联数据库HMDD构建了二部图,我们有![]() <
<![]() 。 换句话说,图上的一些 miRNAs 并不包含在 MISIM 中。 我们稍后将引入高斯互作谱核相似性来解决这个问题。 同样值得一提的是,使用功能相似性假设两个功能相似性强(即
。 换句话说,图上的一些 miRNAs 并不包含在 MISIM 中。 我们稍后将引入高斯互作谱核相似性来解决这个问题。 同样值得一提的是,使用功能相似性假设两个功能相似性强(即![]() 中的一个大条目)的miRNAs往往与具有相似表型的疾病相关。
中的一个大条目)的miRNAs往往与具有相似表型的疾病相关。


2 MeSH is available at https://www.ncbi.nlm.nih.gov/mesh/.
基于![]() 数据库计算疾病语义相似度,提供了一个严格的疾病分类系统。 这个数据库形成了一个有向无环图(DAG)。 每个节点对应一个疾病,子节点到父节点的每个边都提示子疾病属于父疾病(的类)。 对于每个疾病
数据库计算疾病语义相似度,提供了一个严格的疾病分类系统。 这个数据库形成了一个有向无环图(DAG)。 每个节点对应一个疾病,子节点到父节点的每个边都提示子疾病属于父疾病(的类)。 对于每个疾病![]() ,我们用一对
,我们用一对![]()
![]() 来表示节点
来表示节点![]() 诱导的DAG。 特别地,
诱导的DAG。 特别地,![]() 是由
是由![]() 本身及其所有父节点组成的节点集,
本身及其所有父节点组成的节点集,![]() 是
是![]() 对应的边集。 图2显示了食管癌引起的DAG。从图2中我们看到食管癌有三个父节点,分别是食管癌、胃肠道肿瘤和头颈部肿瘤。 这三个母体节点来自两个祖先,即消化系统疾病和肿瘤,我们将在下面的实验和结果部分进行食管癌的案例研究。
对应的边集。 图2显示了食管癌引起的DAG。从图2中我们看到食管癌有三个父节点,分别是食管癌、胃肠道肿瘤和头颈部肿瘤。 这三个母体节点来自两个祖先,即消化系统疾病和肿瘤,我们将在下面的实验和结果部分进行食管癌的案例研究。

原则上,在计算语义相似度时,更具体的疾病可以贡献更多的信息。 对于DAG上的每个节点![]() ,我们将其语义贡献定义为
,我们将其语义贡献定义为

对![]() 中的所有节点贡献求和,我们得到
中的所有节点贡献求和,我们得到![]() 的语义值:
的语义值:

然后,计算![]() 与
与![]() 之间的疾病语义相似度,
之间的疾病语义相似度,![]()

与miRNA的功能相似性类似,我们注意到并不是HMDD中的每一种疾病都包含在MeSH中。 HMDD中的某些疾病可能不出现在DAG上,因此它们与其他疾病在语义上没有相似之处。 我们引入高斯互作谱核相似度来为它们提供特征表示。
我们还注意到前人的工作[1,27,59,60]也采用了类似的方法计算疾病语义相似度。 然而,[21]采用了不同的方式,其中作者将![]() 和
和![]() 之间的语义相似性定义为
之间的语义相似性定义为
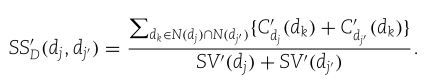
这里,![]() 是
是![]() 对
对![]() 的语义贡献,
的语义贡献,![]() 是
是![]() 的语义值。 它们是由(类似的)计算
的语义值。 它们是由(类似的)计算

其中![]() 是语义衰减因子,
是语义衰减因子,![]() 表示
表示![]() 上
上![]() 与
与![]() 之间的最短路径距离,且
之间的最短路径距离,且![]() 。
。
在我们的实验中,我们比较了三种语义相似度度量:![]() ,
,![]() 及其组合
及其组合![]() 。 我们观察到三种选择得到相似的结果; 没有哪个总是胜过其他的。 因此,考虑到简单性和计算效率,我们在设计中只采用
。 我们观察到三种选择得到相似的结果; 没有哪个总是胜过其他的。 因此,考虑到简单性和计算效率,我们在设计中只采用![]() 作为语义相似度矩阵。
作为语义相似度矩阵。

高斯互作谱核相似性考虑了miRNA-疾病二部图的拓扑信息。 这种相似性的合理性在于,如果两个miRNAs的相关疾病相似(两种疾病相同),它们应该具有相似的特征表示。 特别地,对于每个miRNA节点![]() ,我们设
,我们设![]() 为二进制向量。 如果
为二进制向量。 如果![]() 和
和![]() 是连接的,则它的
是连接的,则它的![]() 条目
条目![]() ,否则
,否则![]() 。 然后,
。 然后,![]() 和
和![]() 之间的高斯互作谱核相似度如下
之间的高斯互作谱核相似度如下
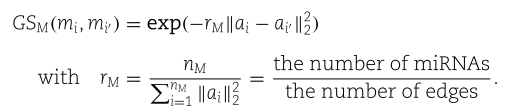
类似地,对于每一个疾病![]() ,设
,设![]() 是二进制向量,如果
是二进制向量,如果![]() 和
和![]() 是连通的,则其
是连通的,则其![]() 项
项![]() ,否则
,否则![]() 。 那么,我们有
。 那么,我们有


特征表示。 我们现在准备为二部图G上的每个节点提供一个特征表示。我们利用上面的三个相似性:![]() 。 对于每个miRNA节点
。 对于每个miRNA节点![]() ,其特征表示
,其特征表示![]() 是一个
是一个![]() 维向量。 它的
维向量。 它的![]() 项计算如下
项计算如下

类似地,对于每个疾病节点![]() ,其特征表示
,其特征表示![]() 是一个
是一个![]() 维向量,
维向量,![]() 项为
项为

Step 2: construct self-feature embeddings

在这一步中,我们为每个miRNA节点![]() 构造自特征嵌入
构造自特征嵌入![]() ,为每个疾病节点
,为每个疾病节点![]() 构造自特征嵌入
构造自特征嵌入![]() 。在这里,
。在这里,![]() 代表SFGAE模型的层数,我们用
代表SFGAE模型的层数,我们用![]() 表示层的总数。在下面的演示中,我们以节点
表示层的总数。在下面的演示中,我们以节点![]() 和
和![]() 为例,说明如何构造
为例,说明如何构造![]() 和
和![]() ,该构造也适用于
,该构造也适用于![]() 和
和![]() 中的其他节点。
中的其他节点。
给定第一步中的特征表示![]() 和
和![]() ,我们首先对它们应用仿射变换来匹配它们的维数。 该变换得到
,我们首先对它们应用仿射变换来匹配它们的维数。 该变换得到![]() 和
和![]() ,我们有
,我们有
![]()

其中![]() 是可训练权重矩阵和偏置向量。 我们强调,对于所有miRNA节点,我们总是使用相同的可训练权重矩阵和偏置向量(这对于疾病节点是一样的,对于下面的设计也是一样的)。 也就是说,
是可训练权重矩阵和偏置向量。 我们强调,对于所有miRNA节点,我们总是使用相同的可训练权重矩阵和偏置向量(这对于疾病节点是一样的,对于下面的设计也是一样的)。 也就是说,![]() 和
和![]() 不随索引
不随索引 ![]() 而变化。 因此,我们的自特征嵌入结构不会增加训练模型的计算成本。
而变化。 因此,我们的自特征嵌入结构不会增加训练模型的计算成本。
在初始的自特征嵌入![]() 和
和![]() 的基础上,我们说明了当模型深入时如何更新它们。我们使用了FCNs。特别地,对于任意
的基础上,我们说明了当模型深入时如何更新它们。我们使用了FCNs。特别地,对于任意![]() 我们有
我们有
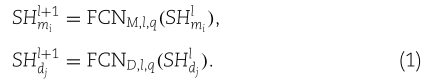

这里,![]() 是保留输入维数
是保留输入维数![]() 的FCN映射;
的FCN映射; ![]() 为FCN中的层数; 而
为FCN中的层数; 而![]() 是模型的层索引值。 在FCN每一层中,我们遵循[1],使用LeaklyRelu作为激活函数。 例如,当
是模型的层索引值。 在FCN每一层中,我们遵循[1],使用LeaklyRelu作为激活函数。 例如,当![]() 时,
时,![]() 的形式为
的形式为
![]()

其中![]() 是模型
是模型![]() 层的可训练权重矩阵和偏置向量。实验表明,
层的可训练权重矩阵和偏置向量。实验表明,![]() 足以保证模型的性能。
足以保证模型的性能。
基于我们的构造(1),每个节点的自特征嵌入更新独立于与其他节点的图交互。 即 miRNA 自特征嵌入![]() 是针对每个
是针对每个![]() 递归定义的,并且不受其他 miRNA 或疾病节点的影响。 疾病自特征嵌入
递归定义的,并且不受其他 miRNA 或疾病节点的影响。 疾病自特征嵌入![]() ,具有类似的性质。 因此,这些自特征嵌入表征了每个节点的唯一性。 正如我们将在第3步中看到的,这种唯一性描述思想与构造聚合特征嵌入的原则形成了对比。 据我们所知,现有文献中缺少对每个节点唯一性的研究。
,具有类似的性质。 因此,这些自特征嵌入表征了每个节点的唯一性。 正如我们将在第3步中看到的,这种唯一性描述思想与构造聚合特征嵌入的原则形成了对比。 据我们所知,现有文献中缺少对每个节点唯一性的研究。
Step 3: construct aggregated feature embeddings


在这一步中,我们为每个miRNA节点![]() 构造了精化的聚集特征嵌入
构造了精化的聚集特征嵌入![]() ,为每个疾病节点
,为每个疾病节点![]() 构造了
构造了![]() 。 我们遵循步骤2中的表示,并将重点放在节点
。 我们遵循步骤2中的表示,并将重点放在节点![]() 和
和![]() 上。 该构造立即应用于集合M和D中的其他节点。
上。 该构造立即应用于集合M和D中的其他节点。

与自特征嵌入不同的是,聚集特征嵌入关注节点间的图交互,是通过聚集直接邻居的所有信息而得到的。 由于二分图的结构,miRNA节点![]() 的直接邻居是疾病节点,疾病节点
的直接邻居是疾病节点,疾病节点![]() 的直接邻居是miRNA节点。 因此,当堆叠更多的层和执行更多次的聚合时,嵌入在不同(类型)的节点之间被平滑,并且丢失了每个节点的唯一性信息。 为了解决这个问题,我们在这一步中利用自特征嵌入来丰富原始聚集特征嵌入的信息。 工作[1]只采用了后一种嵌入方式。
的直接邻居是miRNA节点。 因此,当堆叠更多的层和执行更多次的聚合时,嵌入在不同(类型)的节点之间被平滑,并且丢失了每个节点的唯一性信息。 为了解决这个问题,我们在这一步中利用自特征嵌入来丰富原始聚集特征嵌入的信息。 工作[1]只采用了后一种嵌入方式。

特别地,步骤3包括三个子步骤:构造原始聚集特征嵌入; 构造聚合自特征嵌入; 并在一个注意力机制下结合两种类型的嵌入。 作为一个起点,我们对特征表示![]() 和
和![]() 应用仿射变换来匹配它们的维数。 该变换给出了
应用仿射变换来匹配它们的维数。 该变换给出了![]() 和
和![]() ,我们有
,我们有
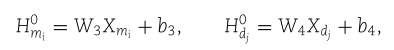

其中![]() 是可训练权重矩阵和偏置向量。 我们还设
是可训练权重矩阵和偏置向量。 我们还设![]()
![]() 为
为![]() 的直接邻居,即与
的直接邻居,即与![]() 有关的所有疾病,并设
有关的所有疾病,并设![]() 为基数。 类似地,我们有
为基数。 类似地,我们有![]() 。
。
现在,给定![]() ,以及
,以及![]() (回想一下,
(回想一下,![]() 索引了模型的层,并且
索引了模型的层,并且![]() 已经从步骤2中获得),我们执行以下三个步骤来获得
已经从步骤2中获得),我们执行以下三个步骤来获得![]() 。
。
Step 3.1: construct primitive aggregated feature embeddings.
我们令


其中![]() 是一个聚合函数。 在给定向量集
是一个聚合函数。 在给定向量集![]() 的情况下,我们在模型中采用了归一化和聚合函数,即
的情况下,我们在模型中采用了归一化和聚合函数,即![]()
![]() 。
。
Step 3.2: construct aggregated self-feature embeddings.
我们令


虽然上述函数![]() 不必与(1)相同,但为了简单起见,我们仍然使用归一化和作为聚合函数。
不必与(1)相同,但为了简单起见,我们仍然使用归一化和作为聚合函数。
Step 3.3: combine under attention mechanism.


第三步:结合注意力机制。 我们将得到的嵌入![]() 融合到两个注意力层(一个针对miRNA,一个针对疾病),对不同的嵌入赋予不同的权重,最终得到精炼的聚合特征嵌入
融合到两个注意力层(一个针对miRNA,一个针对疾病),对不同的嵌入赋予不同的权重,最终得到精炼的聚合特征嵌入![]() 。 特别地,对于miRNA
。 特别地,对于miRNA![]() ,我们计算
,我们计算


其中,![]() 是可训练的权重矩阵和权重向量。 同样,对于疾病
是可训练的权重矩阵和权重向量。 同样,对于疾病![]() ,我们有
,我们有


到目前为止,我们已经构造了聚集特征嵌入![]() 。 步骤2和步骤3构成SFAGE模型的一个GNN层,表示为SFGNN。 当我们堆叠更多的层时,我们简单地重复步骤2和步骤3。 具体而言,miRNA层以
。 步骤2和步骤3构成SFAGE模型的一个GNN层,表示为SFGNN。 当我们堆叠更多的层时,我们简单地重复步骤2和步骤3。 具体而言,miRNA层以![]() 为输入,然后依次进行(1)、(1)、(2)、(3),得到
为输入,然后依次进行(1)、(1)、(2)、(3),得到![]() 。 疾病层以
。 疾病层以![]() 为输入,依次进行(1)、(1)、(2)、(4),得到
为输入,依次进行(1)、(1)、(2)、(4),得到![]() 。 简而言之,我们表示
。 简而言之,我们表示

其中![]() , 我们还在图3中演示了SFGNN层。
, 我们还在图3中演示了SFGNN层。

从特征表示![]() 构造
构造![]() 是 SFAGE 的编码器步骤。我们提出执行两个 SFGNN 层,即 L = 2。但是,考虑到我们设计的灵活性,我们可以简单地堆叠更多层并训练更深的模型。我们将在实验中根据 L 来测试鲁棒性。我们观察到 SFGAE 对 L 是鲁棒的,即使 L 大到 8(或 9)也能稳定地执行,而之前不包括自特征嵌入的工作对 L 不鲁棒。这一观察表明我们的设计有效地克服了过度平滑的问题。
是 SFAGE 的编码器步骤。我们提出执行两个 SFGNN 层,即 L = 2。但是,考虑到我们设计的灵活性,我们可以简单地堆叠更多层并训练更深的模型。我们将在实验中根据 L 来测试鲁棒性。我们观察到 SFGAE 对 L 是鲁棒的,即使 L 大到 8(或 9)也能稳定地执行,而之前不包括自特征嵌入的工作对 L 不鲁棒。这一观察表明我们的设计有效地克服了过度平滑的问题。
Step 4: predict associations

我们将得到的自特征嵌入和精炼的聚集特征嵌入连接起来,并使用标准的双线性译码器进行关联预测,该译码器由一个sigmoid函数卷积,我们采用交叉熵损失。 特别的, 我们有


其中![]() 是可训练权重矩阵;
是可训练权重矩阵; ![]()
![]() ;
;![]() 为真标签,即如果
为真标签,即如果![]() 连接,
连接,![]() ,否则
,否则![]() ; D是包含正样本和负样本的数据集。 整个SFGAE模型通过反向传播进行训练。
; D是包含正样本和负样本的数据集。 整个SFGAE模型通过反向传播进行训练。
Experiments and Results

我们进行了大量的实验来测试SFAGE模型在关联预测任务中的有效性。 我们主要在数据集HMDD V2.0上演示了SFGAE的性能(因为直接相关的模型都应用在HMDD V2.0上),同时我们也在HMDD V3.2上应用了SFGAE来验证SFGAE的优点对于不同的数据集仍然有效。 我们的实验表明,SFGAE在基准数据集上达到了最先进的性能。 它在三种与肿瘤有关的人类疾病的案例研究中预测的关联在生物学实验中得到了很大程度的验证。 因此,SFAGE是预测miRNA与疾病相关性的可靠工具。

在下面的小节中,我们首先介绍了数据集HMDD V2.0,并展示了数据集的一些统计信息。 然后在第二小节中介绍了参数设置和评价指标。 在接下来的七个小节中,我们测试了SFGAE的关键部分,包括采用的语义相似性、构造的自特征嵌入和使用的注意力机制,并通过改变训练样本大小、数据集的不平衡程度、编码层数和嵌入维数来观察参数对SFGAE性能的影响。 在接下来的两小节中,我们将SFGAE与其他相关方法进行比较,并说明SFGAE在HMDD V3.2上的性能。 在最后两个小节中,我们进行案例研究和生存分析。 我们所有的结果都可以在https://github.com/AI-luyuan/SFGAE上复现。 我们的实现是在一台配有4.2GHz Intel Core i7 CPU,32GB RAM和GeForce GTX 1080TI GPU的计算机上进行的。
Dataset

我们主要将SFGAE应用于文献中常用的基准数据集miRNA-疾病关联数据集HMDD V2.0上。 该数据集包含![]() 个miRNAs和
个miRNAs和![]() 个疾病,它们之间有5430个关联。 在此基础上,我们构造了一个二部图G,并在表1中总结了数据集的一些基本统计量,包括节点的平均度(average degree)、接近中心性(closeness centrality)和特征向量中心性(eigenvector centrality)。
个疾病,它们之间有5430个关联。 在此基础上,我们构造了一个二部图G,并在表1中总结了数据集的一些基本统计量,包括节点的平均度(average degree)、接近中心性(closeness centrality)和特征向量中心性(eigenvector centrality)。

从表1中,我们看到miRNA节点的平均度比疾病节点小,而miRNA节点的接近中心度和特征向量中心度比疾病节点大。 在实验中,我们将所有已知的关联(即总共5430个关联)作为正样本,从未知或缺失的关联中抽取另外5430个关联作为负样本。 正样本和负样本构成完整的数据集。

Parameter setups and evaluation metrics


遵循文[1]提出的GAEMDA模型,在MXNet后端实现了基于深度图形库(Deep Graph Library)的SFGAE。 MXNet是一个为分布式系统设计的深度学习库,具有轻量级和可移植性等优点。 我们用Adam[62]优化可训练模型变量。 为了避免过拟合,我们采用了标准的dropout技术。 特别地,在训练阶段,我们随机丢弃仿射变换后的隐藏单元和每个完全连接的层,我们执行网格搜索来选择超参数。 最后,我们设定学习率为0.001,权值衰减为2e-3,dropout率为0.7。 我们还设置FCN层数 q=1 ,GNN层数 L=2 ,嵌入维数P=256。 随后对这三个参数的影响进行了测试。 我们对模型进行了100个epochs的训练,根据前人的工作[1],将语义衰减因子δ=0.5,将负值的LeaklyreLu斜率设为0.2。该模型对每个miRNA-疾病对的潜在边缘输出的概率在0到1之间。 我们使用0.5作为链路预测的阈值。如果概率大于或等于0.5,我们预测该对是链接的(即为正对); 否则,该对是未链接的。 在本文中,我们使用五折交叉验证来评估性能。 具体地说,将数据集中的所有样本分成五个大小相等的子集。 重复实现五次,每个子集依次作为测试集,其余四个子集作为训练集,然后报告以下五个指标中每一个指标的平均值。

我们采用了五个常用的评价指标来衡量性能:接收机工作特性曲线下面积(AUC)、准确性、查准率、查全率和F1得分。 AUC描述了模型对正样本的排名高于负样本的概率。 一般来说,较大的AUC意味着较好的性能。 其他四个评估指标计算如下:

其中TN、TP、FN、FP分别表示真阴性、真阳性、假阴性和假阳性。
Effect of semantic similarities


如步骤1(Step 1)中所介绍的,现有文献介绍了三种疾病语义相似度矩阵:![]()
![]()
![]() 我们比较了SFGAE实现中的三种选择。 结果汇总在表2中。 从表2中我们可以看出,在SFGAE中采用不同的语义相似性不会对结果产生太大的影响。 特别是
我们比较了SFGAE实现中的三种选择。 结果汇总在表2中。 从表2中我们可以看出,在SFGAE中采用不同的语义相似性不会对结果产生太大的影响。 特别是![]() 达到了最高的 Accuracy 和 F1-score ;
达到了最高的 Accuracy 和 F1-score ;![]() 达到最高 Recall ; 而
达到最高 Recall ; 而![]() (即默认设置)实现了最高的 Precision 和 AUC。 然而,大多数指标的差异都在0.05%以内。 正如在以后的实验中所研究的那样,如此微小的差异并不会导致对所提出的SFGAE模型的任何不同结论。 另一方面,由于
(即默认设置)实现了最高的 Precision 和 AUC。 然而,大多数指标的差异都在0.05%以内。 正如在以后的实验中所研究的那样,如此微小的差异并不会导致对所提出的SFGAE模型的任何不同结论。 另一方面,由于![]() 的计算效率高于其他两个选择(
的计算效率高于其他两个选择(![]() 需要计算两个语义相似度,
需要计算两个语义相似度,![]() 需要计算DAG上的最短路径),所以我们倾向于只采用
需要计算DAG上的最短路径),所以我们倾向于只采用![]() 来度量疾病语义相似度。
来度量疾病语义相似度。
Effect of self-feature embeddings
我们测试了所提出的自特征嵌入的效果。 我们证明了在GNN模型中引入自特征嵌入确实显著地提高了模型的性能。 虽然我们设置了FCN层数![]() ,但我们也测试了这个参数的影响,并表明我们的SFGAE模型对这个参数是鲁棒的。
,但我们也测试了这个参数的影响,并表明我们的SFGAE模型对这个参数是鲁棒的。
为此,除了SFGAE之外,我们还考虑了另外三种模型:无miRNA自特征嵌入的SFGAE、无疾病自特征嵌入的SFGAE和无miRNA和疾病自特征嵌入的SFGAE。 我们将前两个模型称为![]() 。 对于最后一个模型,它自动归结为[1]中提出的GAEMDA模型。 这是由于删除所有自特征嵌入导致我们也删除注意力层。 四种模型的实验结果如表3所示。
。 对于最后一个模型,它自动归结为[1]中提出的GAEMDA模型。 这是由于删除所有自特征嵌入导致我们也删除注意力层。 四种模型的实验结果如表3所示。

从表3中,我们看到SFGAE在Accuracy、Precision、F1-Score和AUC方面表现最好。 SFGAE比GAEMDA有显著的改进。 SFGAE的平均度量比GAEMDA高至少一个(或甚至两个,例如,对于Precision)标准偏差。 例如,GAEMDA的F1得分为0.8575,而SFGAE的F1得分为0.8678。 差值大于0.0076,0.0076为GAEMDA的标准差。 此外,我们发现miRNA-自特征嵌入(SF-D)或疾病自特征嵌入(SF-M)的模型在Accuracy、precision、F1-score和AUC等指标上也优于GAEMDA,尽管它们的表现不如SFGAE。 这一观察得出结论,我们的自特征嵌入有助于增强GNN模型的性能。 我们还应该提到,GAEMDA实现了比SFGAE更高的 Recall 。 简单模型SF-M和SF-D的 Recall 也略高于完整的SFGAE模型。 基于 Recall 和 Precision 的定义,我们推导出SFGAE和GAEMDA分别具有较少的假阳性和假阴性。 鉴于我们希望为指导生物实验的验证提供证据,较少的假阳性表明SFGAE往往比GAEMDA提供更强的证据。 另一方面,后者有更好的能力不遗漏任何潜在的有效miRNAs。 为了进一步研究 Recall 和 Precision 指标,我们改变分类阈值并绘制图4中的PR曲线。 我们还报告了不同阈值下的最大F1得分。 从图中我们可以看到SFGAE具有最好的AUPR值(即PR曲线下的面积)和F1-score。

现在,我们改变FCN层数![]() ,设
,设![]()
![]() ,并将结果总结在表4和图5中。当
,并将结果总结在表4和图5中。当![]() 时,不更新自特征嵌入(即
时,不更新自特征嵌入(即![]() )。 在这种情况下,我们只使用
)。 在这种情况下,我们只使用![]() 。 当
。 当![]() 时,我们到达默认设置,结果与表3一致。 如表4和图5所示,SFGAE对于不同的
时,我们到达默认设置,结果与表3一致。 如表4和图5所示,SFGAE对于不同的![]() 选择表现鲁棒。当
选择表现鲁棒。当![]() 设为1得到最高的 Accuracy , AUC 和 Precision;
设为1得到最高的 Accuracy , AUC 和 Precision;![]() =0 的设置获得最高的 F1-score ; 其中
=0 的设置获得最高的 F1-score ; 其中![]() =4的得到最好的 Recall 。值得注意的是,
=4的得到最好的 Recall 。值得注意的是,![]() 的七种不同设置都导致 SFGAE 在Accuracy、Precision、F1-score 和 AUC 等方面都比GAEMDA有更好的表现。 这一观察表明,SFGAE对GAEMDA 的改善不是由于特定的
的七种不同设置都导致 SFGAE 在Accuracy、Precision、F1-score 和 AUC 等方面都比GAEMDA有更好的表现。 这一观察表明,SFGAE对GAEMDA 的改善不是由于特定的![]() 选择; 相反,对于不同的
选择; 相反,对于不同的![]() 值,都有改进。 我们将在接下来的实验中进一步考察GNN层数L的影响。 我们证明了SFGAE使模型能够更深,从而有效地克服了过平滑问题。
值,都有改进。 我们将在接下来的实验中进一步考察GNN层数L的影响。 我们证明了SFGAE使模型能够更深,从而有效地克服了过平滑问题。


Effect of attention mechanism
我们现在测试所采用的注意机制的效果(参见(3)和(4))。 除了SFGAE和基线GAEMDA外,我们还考虑了另外两个模型:![]() ,它们分别用求和函数和最大值函数代替(3)和(4)中的加权和。 结果如表5所示。 从表5中,我们看到SFGAE在Accuracy、Precision、F1-score和AUC指标上优于
,它们分别用求和函数和最大值函数代替(3)和(4)中的加权和。 结果如表5所示。 从表5中,我们看到SFGAE在Accuracy、Precision、F1-score和AUC指标上优于![]() ,这三种注意力机制的模型在相同的指标上均优于GAEMDA。 例如,
,这三种注意力机制的模型在相同的指标上均优于GAEMDA。 例如,![]() 在三款新模型中 F1-score 最低,但仍比GAEMDA高出一个标准差(但在两个标准差内)。 与表3类似,我们看到GAEMDA与其他三个模型相比实现了最好的 Recall。 然而,鉴于这三个模型在五个指标中有四个指标获得了更好的分数(而且Precision的提高是显著的),我们可以得出结论,注意力机制有助于提高GAEMDA的性能。 特别是所采用的注意机制(即,使用加权和函数 )实现性能的最高提升。
在三款新模型中 F1-score 最低,但仍比GAEMDA高出一个标准差(但在两个标准差内)。 与表3类似,我们看到GAEMDA与其他三个模型相比实现了最好的 Recall。 然而,鉴于这三个模型在五个指标中有四个指标获得了更好的分数(而且Precision的提高是显著的),我们可以得出结论,注意力机制有助于提高GAEMDA的性能。 特别是所采用的注意机制(即,使用加权和函数 )实现性能的最高提升。

Effect of training sample sizes
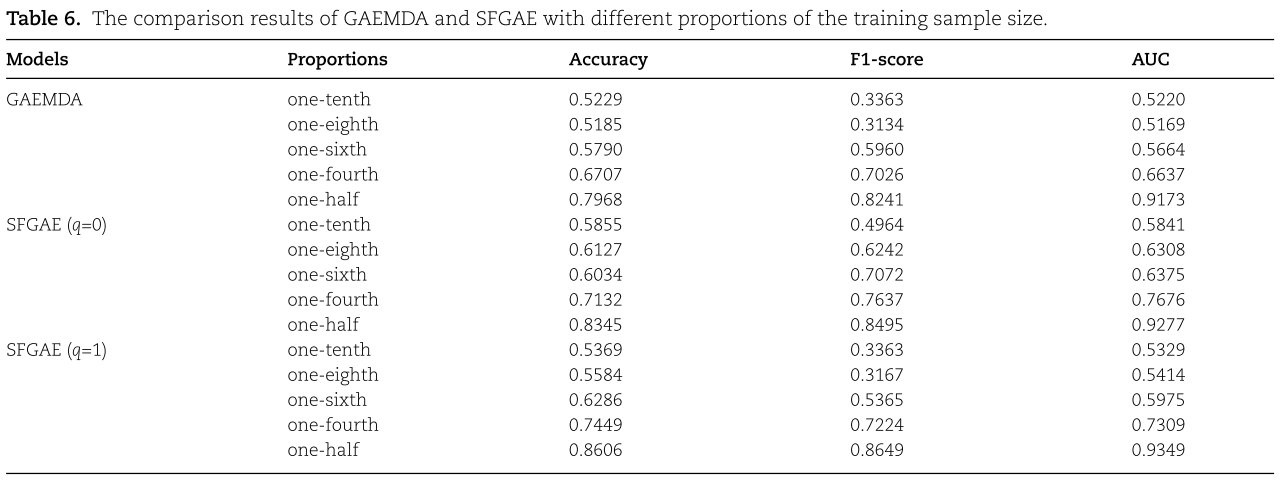
我们现在测试了SFGAE的样本效率(sample efficiency),并与GAEMDA进行了比较。 特别地,我们在集合{1/10,1/8,1/6,1/4,1/2}内改变训练样本量与全样本量的比例。 例如,当将训练样本作为全样本的十分之一时,我们将全数据集随机分成10个大小相等的子集。 重复实现10次,每个子集依次作为训练集重新分级,其余9个子集作为测试集。 我们注意到,这样的实现过程与10倍交叉验证形成鲜明对比,其中每次使用9个子集作为训练集,使用一个子集作为测试集。 我们提到,由于整个数据集是随机划分的,每个子集仍然是平衡的(即它大致具有相同数量的正负样本)。 我们将在下一小节研究不平衡数据集。
实验结果总结在表6中。从表6中,我们观察到,对于GAEMDA和SFGAE,当训练样本容量占较大比例时,Accuracy、F1-score和AUC的度量值都较高。 当比例从十分之一变为二分之一的改善对这两种方法来看是显著的,这与我们的一般直觉是一致的。 此外,我们观察到SFGAE在五种不同比例下的accuracy、F1评分和AUC方面都优于GAEMDA。 例如,当仅使用四分之一样本作为训练样本时,SFGAE(q=1)将GAEMDA的正确率从67.07%提高到74.79%。 SFGAE(q=0)使F1-score由70.26%提高到76.37%,AUC由66.37%提高到76.76%。 这些度量标准大约提高了7%到10%。 通过实验,我们可以得出SFGAE在从大镜头到少镜头的不同数据级别上都有很好的稳定性能。
Effect of imbalance of dataset
我们在不平衡数据集上进行了实验。 我们从集合{1/2,1/6,1/10}中改变正样本与负样本的比例。 例如,当阳性样本是阴性样本的十分之一时,我们将所有已知的关联(即总共5430个关联)视为阳性样本,并从未知或缺失的关联中再抽取54 300个关联作为阴性样本。 我们一直使用五折交叉验证来评估性能。 然而,由于数据集是高度不平衡的,我们提供了一个新的度量,即PR曲线下的面积(AUPR),这是在这种情况下更常用的度量。
结果汇总在表7中。 我们观察到SFGAE在Accuracy、AUC和AUPR方面优于GAEMDA。 尤其是AUPR的差异在阳性样本比例下降时更为明显。 例如,当阳性样本的比例为十分之一时,SFGAE(q=0)将GAEMDA的AUPR从66.94%提高到68.04%,SFGAE(q=1)将AUPR从66.94%提高到68.18%。 两个差异均大于1.1%。 然而,我们应该提到,SFGAE和GAEMDA之间的性能差异仍然很小(没有平衡数据集上的差异那么显著)。 其原因是数据集的高度不平衡给分类任务带来了内在的挑战,通常需要一个ad hoc模型设计来处理这种不平衡。 从这个意义上说,SFGAE和GAEMDA都必须以特定的方式进行调整,以便更适合不平衡的数据集。

Effect of the number of encoder layers
正如在引言部分所提到的,基于GNN的方法经常被过平滑问题所困扰。 当模型深入时,不同类型节点的学习嵌入相似,导致预测精度较低。 在本节中,我们将对这一问题进行研究。
我们将GAEMDA与SFGAE(q=1)(我们的默认设置)和SFGAE(q=0)进行了比较。 对于所有模型,我们将GNN层数L在{4,5,6,7,8}范围内改变。 当L变大时,模型变深。 AUC和F1-score如图6所示。 从图6中,我们可以看到SFGAE(q=0)和SFGAE(q=1)即使在L大到8的情况下也能很好地稳定工作。 特别地,SFGAE(q=0)的AUC在94.02%-94.05%的范围内变化,SFGAE(q=1)的AUC在93.54%-93.68%的范围内变化。 而对于模型GAEMDA而言,当L小于7时,AUC度量高达93.2%(比SFGAE略差)。 当L为8时,AUC指标立即下降到81.48%。 F1-score指标也有同样的趋势。 因此,正如[1]所承认的,GAEMDA不适合深层模型。相比之下,从表3、表5和图6来看,我们构造的自特征嵌入和使用的注意力机制不仅提高了GAEMDA在浅层模型(如L=2)上的性能,而且使这种改进推广到深层模型(如L=8)上。 因此,我们得出结论:SFGAE有效地克服了过平滑问题,并且对GNN层数具有更强的鲁棒性。

Effect of embedding dimensions
我们现在测试嵌入维数![]() 对SFGAE的影响。 我们设
对SFGAE的影响。 我们设![]() 。 结果如图7所示。 从图7中,我们观察到AUC、Accuracy和F1-score指标随着
。 结果如图7所示。 从图7中,我们观察到AUC、Accuracy和F1-score指标随着![]() 的增大而逐渐增加,而 Precision 和 Recall 指标在
的增大而逐渐增加,而 Precision 和 Recall 指标在![]() 方面没有明显的变化趋势。 然而,即使
方面没有明显的变化趋势。 然而,即使![]() 在32~512之间变化,所有指标的变化也不显著。 例如,Precision 指标在83.42%–85.53%范围内变化。即便最低的 Precision 值(对应于p的设置小到32)仍然高于GAEMDA(参见表3),后者将嵌入维度设置为256(此设置与我们的默认设置相同)。 因此,我们得出结论:SFGAE对GAEMDA的改进并不是由于嵌入维数
在32~512之间变化,所有指标的变化也不显著。 例如,Precision 指标在83.42%–85.53%范围内变化。即便最低的 Precision 值(对应于p的设置小到32)仍然高于GAEMDA(参见表3),后者将嵌入维度设置为256(此设置与我们的默认设置相同)。 因此,我们得出结论:SFGAE对GAEMDA的改进并不是由于嵌入维数![]() 的特定设置,SFGAE的优越性能对嵌入维数的是鲁棒的。 我们注意到在[1]中也对GAEMDA的嵌入维数进行了类似的敏感性研究。 作者将p从32变化到256,并提到p=512由于梯度消失问题而导致性能差(参见[1]中的图3)。 相比之下,
的特定设置,SFGAE的优越性能对嵌入维数的是鲁棒的。 我们注意到在[1]中也对GAEMDA的嵌入维数进行了类似的敏感性研究。 作者将p从32变化到256,并提到p=512由于梯度消失问题而导致性能差(参见[1]中的图3)。 相比之下,![]() =512的SFGAE仍然适用,并取得了令人满意的性能。 此外,我们还观察了GAEMDA的AUC,它更全面地反映了模型的预测性能[1],对于每个嵌入维数来说,GAEMDA的AUC比SFGAE的AUC都要低。 这一观察再次证明了我们设计的优越性。
=512的SFGAE仍然适用,并取得了令人满意的性能。 此外,我们还观察了GAEMDA的AUC,它更全面地反映了模型的预测性能[1],对于每个嵌入维数来说,GAEMDA的AUC比SFGAE的AUC都要低。 这一观察再次证明了我们设计的优越性。

Comparison of SFGAE with other related methods
我们将SFGAE与其他最新的先进方法进行了比较,并证明了SFGAE具有较好的性能。 特别地,我们考虑除了表8中列出的GAEMDA之外的其他七种方法。 为了进行公平的比较,我们在HMDD V2.0数据集上对所有方法进行了5折交叉验证。 因为这些方法采用了不同的度量标准,我们使用AUC作为统一的度量标准来衡量性能。 我们注意到在[1]中也作过同样的比较; 因此,我们从这项工作中引用了有竞争力的方法的结果。 结果汇总在表9中。 (我们记得GAEMDA的其他度量指标已经在表3中显示。)从表9中,我们观察到GAEMDA通过将AUC至少提高0.32%而优于其他基线方法,而SFGAE通过将AUC进一步提高0.63%而优于GAEMDA。 因此,我们可以认为SFGAE在关联预测任务上达到了最先进的性能,对现有的方法有很大的改进。 SFGAE的优势在于其新颖的自特征嵌入和所设计的注意力机制。


Performance of SFGAE on HMDD v3.2
到目前为止,我们在HMDD V2.0数据集上主要应用SFGAE,因为GAEMDA和其他基线方法都是在HMDD V2.0数据集上应用的。 为了说明SFGAE对miRNA与疾病关联不敏感的优势,并探索SFGAE的泛化能力,我们将SFGAE应用于2019年推出的最新版本HMDD数据集HMDD V3.2上。 我们遵循类似的二部图的构造步骤,尽管关联关系在新的数据集中得到了广泛的丰富。 我们还在HMDD V3.2上实现了GAEMDA,并继续使用五折交叉验证来评估所有的方法。 为了提供一些统计观点,并查看GAEMDA和SFGAE之间的差异是否在统计上显著,我们执行t检验。 结果汇总在表10中。
从表10中,我们观察到![]() 在Accuracy和AUC方面都优于GAEMDA,并且在t检验的
在Accuracy和AUC方面都优于GAEMDA,并且在t检验的![]() 小于0.001时,这种改进具有统计学意义。 F1-score无显著差异。 另一方面,
小于0.001时,这种改进具有统计学意义。 F1-score无显著差异。 另一方面,![]() 在所有三个指标上都优于GAEMDA,而在AUC上的改进最显著,在F1-score上的改进最不显著。 总的来说,我们可以说,我们的模型设计的优越性仍然保持在HMDD V3.2上。
在所有三个指标上都优于GAEMDA,而在AUC上的改进最显著,在F1-score上的改进最不显著。 总的来说,我们可以说,我们的模型设计的优越性仍然保持在HMDD V3.2上。

在第六小节(参见表6)之后,我们还在HMDD V3.2上测试了SFGAE的样本效率。 结果如表11所示。 从表11中,我们看到了与表6相似的趋势,即在从十分之一到二分之一的不同数据级别上,SFGAE在Accuracy、F1-score和AUC方面的表现始终优于GAEMDA。 只有两个例外:当训练集的比例为二分之一时,GAEMDA的F1-score和AUC略好于SFGAE的两个变量。 另一方面,我们认识到对于![]() 的SFGAE在某些情况下的改进是非常显著的。 例如,当仅使用十分之一的样本进行训练时,Accuracy、F1-score和AUC分别比GAEMDA提高了14%、35%和16%。 因此,当训练样本非常有限时,我们倾向于采用一种更简单的SFGAE设计(q=0,即通过仿射变换简单地获得自特征嵌入)。
的SFGAE在某些情况下的改进是非常显著的。 例如,当仅使用十分之一的样本进行训练时,Accuracy、F1-score和AUC分别比GAEMDA提高了14%、35%和16%。 因此,当训练样本非常有限时,我们倾向于采用一种更简单的SFGAE设计(q=0,即通过仿射变换简单地获得自特征嵌入)。

我们还改变了GNN层数L于{7,8,9,10,11},并在图8中绘制了AUC和F1-score。从图8中,我们看到SFGAE在这两个度量上表现稳定良好。 对于SFGAE(q=0),AUC和F1-score在91.42%-91.46%和83.46%-83.8%之间变化。 对于SFGAE(q=1),其变化范围分别为89.89%~91.45%和77.03%~83.28%。 而对于GAEMDA来说,当L小于8时,AUC可高达89.53%(略差于SFGAE)。 当L=9时,它立即下降9%至80.11%(与F1-score相似)。 此外,当L=10或11时,由于梯度消失,GAEMDA不能训练到最优(参见相同情况下嵌入维数的影响)。 总的来说,GAEMDA会遇到过平滑的问题,而SFGAE在HMDD V3.2上仍然可以有效地克服这一问题。

Case studies
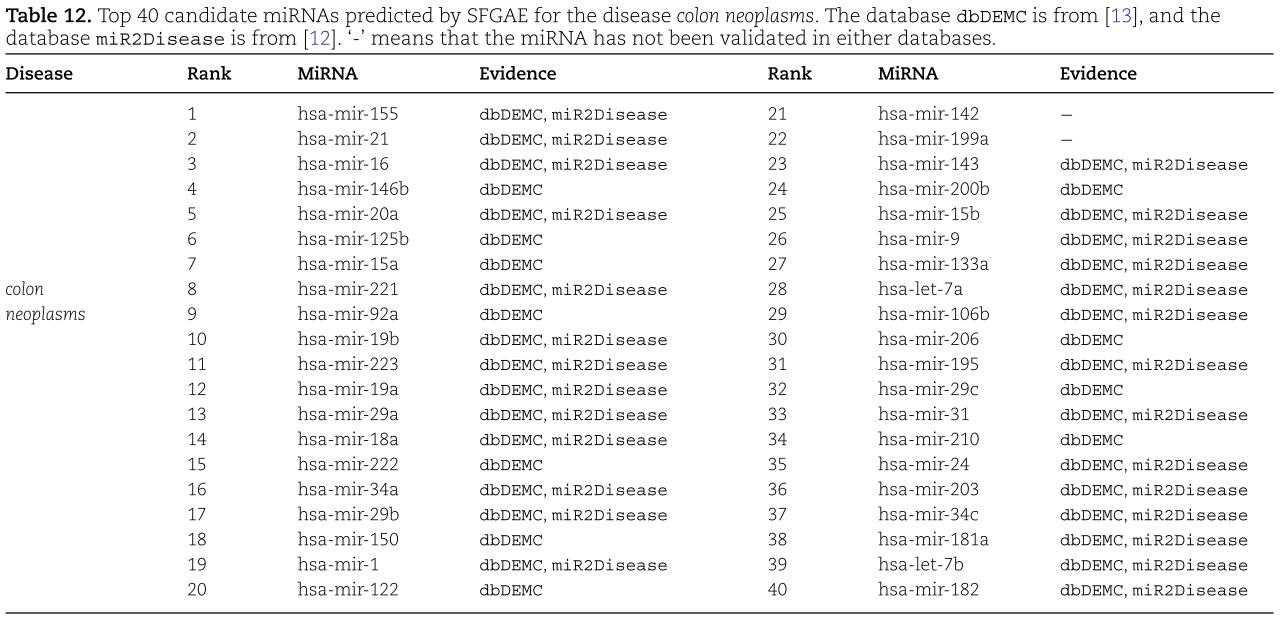
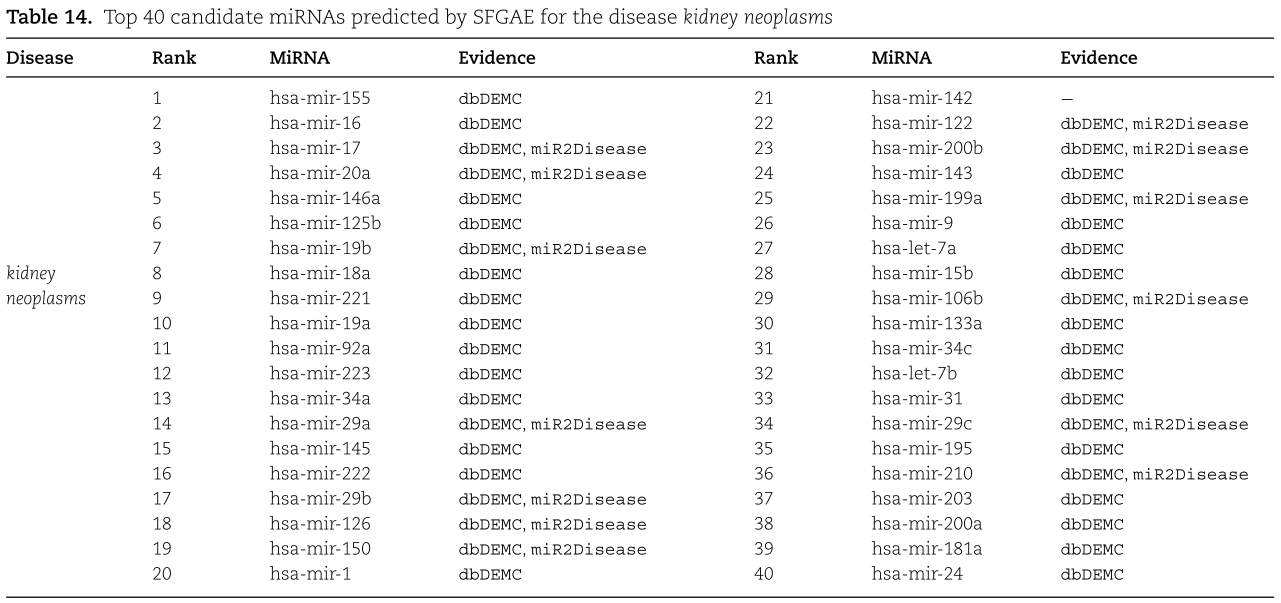
为了进一步说明所提出的SFGAE模型的现实价值,我们现在对三种重要的人类疾病进行案例研究:结肠肿瘤、食管癌和肾肿瘤。 在前文[1]的基础上,对训练集和测试集的构造进行了调整。 特别是,该训练集包含所有实验验证的关联(即总共5430个关联)作为阳性样本,并包含从未知关联中随机选择的5430个关联作为阴性样本,与以前不同的是,它排除了病例研究中调查的特定疾病。 测试集包含特定疾病的所有未知关联。 实验中,我们在训练集上训练SFGAE,得到训练后的权重矩阵,以及特定疾病和所有miRNAs的嵌入然后通过将训练后的权矩阵嵌入到译码器中,在测试集上计算预测的关联概率。然后通过将训练后的权重矩阵和嵌入插入到译码器中,在测试集上计算预测的关联概率。
我们对预测的概率进行排序,并在表12、13和14中提供了前40个候选miRNAs。根据结果,我们看到在结肠肿瘤、食管肿瘤和肾肿瘤的前40个预测miRNAs中,有38、39和39个也被dbDEMC[13]和/或miR2Disease[12]数据库实验验证。 因此,我们认为SFGAE是预测miRNA与疾病关联的可靠工具。

Survival analysis
生存分析是对上一节个案研究的跟进分析,进一步评估 SFGAE 的预测能力。这种类型的分析研究预测的miRNAs与患者生存期之间的关系。 我们以肾肿瘤,特别是透明细胞肾细胞癌为例。 对于每一个前40名候选miRNA,我们有两组患者,一组高表达水平,另一组低表达水平。 对于每一组,我们计算随时间(以天为单位)变化的生存概率。我们还进行测试,看看两组之间的差异是否显著。 我们基于TCGA-KIRC数据集,该数据集可在R包TCGAbiolinks中获得。
我们的实验表明,在40个预测的miRNAs中,有18个![]() 小于0.05。 换句话说,几乎一半的预测miRNAs在导致高表达和低表达组之间的差异方面具有统计学意义 。我们还绘制了图9中显着 miRNA 的存活概率与时间(以天为单位)的图。我们以has-mir-9、hsa-mir-18a、hsa-mir-223、hsa-mir-34c为例,并在线提供了其他miRNAs的图谱。 通过图9,我们知道hsa-miR-223高表达组的生存概率在1700天(4.5年)后下降到0.5以下,而低表达组的生存概率超过3500天(9.5年)。 也就是说,低表达患者的寿命是字面上的两倍。 类似的趋势也适用于其他miRNAs。 鉴于如此显著的差异,我们的生存分析进一步解释了SFGAE的有用性。
小于0.05。 换句话说,几乎一半的预测miRNAs在导致高表达和低表达组之间的差异方面具有统计学意义 。我们还绘制了图9中显着 miRNA 的存活概率与时间(以天为单位)的图。我们以has-mir-9、hsa-mir-18a、hsa-mir-223、hsa-mir-34c为例,并在线提供了其他miRNAs的图谱。 通过图9,我们知道hsa-miR-223高表达组的生存概率在1700天(4.5年)后下降到0.5以下,而低表达组的生存概率超过3500天(9.5年)。 也就是说,低表达患者的寿命是字面上的两倍。 类似的趋势也适用于其他miRNAs。 鉴于如此显著的差异,我们的生存分析进一步解释了SFGAE的有用性。
Conclusion
我们提出了一种新的基于自特征的图自动编码模型来预测miRNAs与疾病之间的关联,简称为SFGAE。 SFGAE的关键部分是自特征嵌入的构造以及自特征嵌入与典型聚集特征嵌入的结合。 特别地,我们采用FCNs获得自特征嵌入,然后利用这些自特征嵌入在注意力机制下对典型的聚集特征嵌入进行精炼。 通过大量的实验,我们测试了SFGAE关键组件的有效性。 我们观察到SFGAE在基准数据集HMDD V2.0和HMDD V3.2上达到了最先进的性能。 SFGAE改进了GAEMDA模型在不同指标上的性能,包括Accuracy、AUC、Precision和F1-score。 SFGAE具有采样效率高的优点,更重要的是,它有效地克服了困扰大多数基于GNN的方法的过平滑瓶颈。 我们对三种疾病进行了案例研究,观察到几乎所有SFGAE预测的每种疾病相关的前40个miRNAs也都得到了生物学实验的证实。 我们还以肾肿瘤为例进行了生存分析。 总体而言,SFGAE可以在实践中可靠地部署。
然而,SFGAE也有局限性。 在一些实验中,它没有达到GAEMDA那样高的Recall。 换句话说,使用所提出的自特征嵌入有时会导致假阴性的增加。 在某些特殊情况下,假阴性得到控制是很重要,如何在不影响Recall的前提下构建替代性的自特征嵌入值得我们进一步研究。 例如,[47]利用每个core and coritivity of each node 作为新的特征,并表明这些特征有助于新的推荐。 The core and coritivity quantities度量了每个结点对全异构图的重要性。 它们是否是二分图上每个结点唯一性的合理替代度量,以及是否有助于克服过光滑问题,有待进一步研究。


Data availability
The implementation of SFGAE is freely available at https://github.com/AI-luyuan/SFGAE.








 本文提出了一种名为SFGAE的新模型,用于miRNA-disease关联预测。SFGAE通过自特征嵌入和注意力机制解决了现有图神经网络模型的过平滑问题,提高了预测准确性。在HMDDV2.0和HMDDV3.2数据集上的实验表明,SFGAE在准确性、AUC和F1得分上优于先前方法,且在不同数据规模、不平衡数据集和深层模型上表现稳定。此外,SFGAE在个案研究和生存分析中也显示了其预测的可靠性。
本文提出了一种名为SFGAE的新模型,用于miRNA-disease关联预测。SFGAE通过自特征嵌入和注意力机制解决了现有图神经网络模型的过平滑问题,提高了预测准确性。在HMDDV2.0和HMDDV3.2数据集上的实验表明,SFGAE在准确性、AUC和F1得分上优于先前方法,且在不同数据规模、不平衡数据集和深层模型上表现稳定。此外,SFGAE在个案研究和生存分析中也显示了其预测的可靠性。
 https://academic.oup.com/bib/article/23/5/bbac340/6678419?login=true
https://academic.oup.com/bib/article/23/5/bbac340/6678419?login=true
















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








