第一次看这题的时候没有好好注意,后来发现这是一类大问题,学习了卡特兰数这个概念,顺便又复习了高中的排列组合知识、、、
一、书中问题
先看一下书中引入卡特兰数的例子:
《编程之美》4.3买票找零:2n个人排队买票,其中n个人持50元,n个人持100元。每张票50元,且一人只买一张票。初始时售票处没有零钱找零。请问这2n个人一共有多少种排队顺序,不至于使售票处找不开钱?
分析1:队伍的序号标为0,1,…,2n-1,并把50元看作左括号,100元看作右括号,合法序列即括号能完成配对的序列。对于一个合法的序列,第0个一定是左括号,它必然与某个右括号配对,记其位置为k。那么从1到k-1、k+1到2n-1也分别是两个合法序列。那么,k必然是奇数(1到k-1一共有偶数个),设k=2i+1。那么剩余括号的合法序列数为f(2i)*f(2n-2i-2)个。取i=0到n-1累加即:
f(2n)=f(0)*f(2n-2)+f(2)*f(2n-4)+······+f(2n-4)*f(2)+f(2n-2)*f(0)
并且令f(0)=1,再由组合数C(0,0)=0,可得
以上就是一种卡特兰数的通项公式,下面具体介绍一下卡特兰数。
二、卡特兰数
1、定义:
以下是百度百科中的定义:卡特兰数又称卡塔兰数,英文名Catalan number,是组合数学中一个常出现在各种计数问题中出现的数列。以比利时的数学家欧仁·查理·卡塔兰 (1814–1894)的名字来命名,其前几项为 : 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, …
2、通项公式
我接触到的公式的定义有两种形式&#








 本文探讨了卡特兰数在编程问题中的应用,如买票找零问题、括号化问题和多边形划分等。通过定义、通项公式和递推关系,解释了卡特兰数如何解决涉及成对元素和特定顺序限制的问题。同时,介绍了如何区分使用f(2n)和f(n)公式,并举例说明了如何将实际问题转化为卡特兰数问题。
本文探讨了卡特兰数在编程问题中的应用,如买票找零问题、括号化问题和多边形划分等。通过定义、通项公式和递推关系,解释了卡特兰数如何解决涉及成对元素和特定顺序限制的问题。同时,介绍了如何区分使用f(2n)和f(n)公式,并举例说明了如何将实际问题转化为卡特兰数问题。
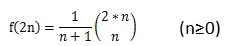
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 5895
5895

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








