今天下午的一会看了对数的知识,因为复杂度中经常会用到对数级别的复杂度。
先看一个对数的公式吧:
今天下午我盯着这个公式看了半天,想知道这个公式是怎么得来的,甚至还花了图,但最后感觉心里还不是很透彻……
然后我又一次感觉到:理解数学中的一些东西,真不是靠画图去理解的,那些数学好的人,肯定也不是这样学数学的。
但我真的很想把数学学好啊……
—— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— ——
还是看一下百度百科上是怎么推导上面的公式的吧:
原来是这样推导而来的。其实很多数学公式就是一层层的推导而来的,是没法画图去解释的。
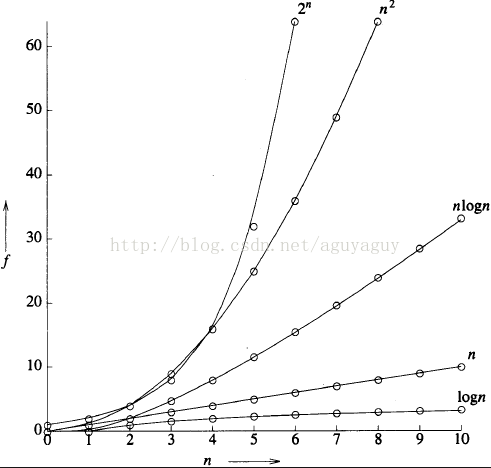
再说说法复杂度吧,看下图:
我们可以看到,图中对数级别的复杂度是最低的,而指数级(即2的n次方)的复杂度最高,其实阶乘的复杂度比指数级还高:
2的n次方:如2的6次方 = 64
1到6的阶乘:1*2*3*4*5*6 = 720
而对数,其实就是指数运算的逆运算:如2的6次方等于64,而log264=6
除了O(1)复杂度,对数复杂度,就已经是查找时间最快的了吧。








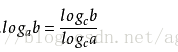

















 1298
1298

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








