快速理解压缩感知

一、压缩感知的原理

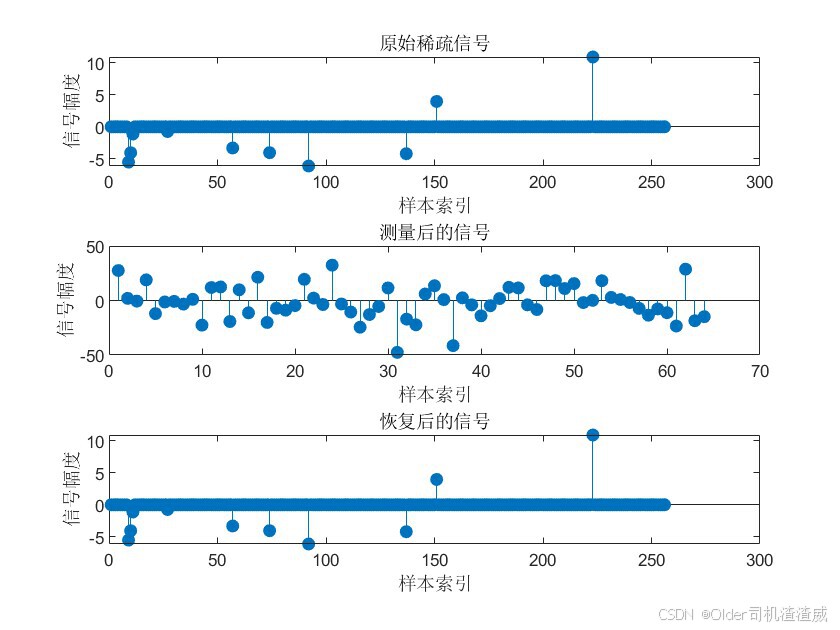
        压缩感知（Compressed Sensing, CS）是一种基于稀疏表示的采样理论，也被称为压缩采样或稀疏采样。它通过利用信号的稀疏性，在远低于传统采样要求的速率下捕获和重构信号。信号的稀疏性是指信号可以在某个变换域内表示为仅有少量非零系数的向量。压缩感知正是基于这一特性，通过寻找最少量的线性测量来重构原始信号。

1. 信号的稀疏性

        信号的稀疏性是压缩感知的基础。稀疏性意味着信号在某个特定的变换域（如傅里叶变换、小波变换、离散余弦变换等）中，大部分系数为零或接近零，只有少数系数具有显著值。这种稀疏表示可以极大地减少信号处理的复杂度，并提高信号重构的准确性。

2. 测量矩阵

        在压缩感知中，信号通过测量矩阵进行采样。测量矩阵的设计是关键环节之一，它要求与信号所在的稀疏空间不相关。常用的测量矩阵包括随机高斯矩阵、随机伯努利矩阵和部分傅里叶矩阵等。这些矩阵能够有效地捕获信号中的稀疏成分，为后续的信号重构提供足够的信息。

3. 信号重构

        信号重构是压缩感知的核心任务。在已知测量矩阵和测量值的情况下，通过求解一个优化问题来找到信号的稀疏表示，然后利用这个稀疏表示重构出原始信号。常用的重构算法包括正交匹配追踪（Orthogonal Matching Pursuit, OMP）、基追踪（Basis Pursuit, BP）和迭代阈值法等。这些算法能够在保证重构精度的同时，降低计算复杂度。

二、压缩感知的主要应用

        压缩感知作为一种革命性的信号处理方法，在多个领域得到了广泛应用。以下是一些主要的应用领域：

1. 图像处理

        在图像处理中，压缩感知可以用于图像的压缩、去噪和超分辨率重建等任务。通过将图像表示为稀疏形式，并利用测量矩阵进行采样，可以极大地降低图像的存储和传输成本。同时，通过重构算法可以恢复出高质量的图像，提高图像的视觉效果。