统一场论中的“动量强守恒”—— 定义、原理及数值验证
摘要: 本文深入探讨张祥前统一场论(简称“统一场论”)的核心概念——“动量强守恒”,明确其与传统动量守恒的根本差异,系统阐述其公设基础与理论推导,通过数值分析验证其数学自洽性,并探讨其与主流物理学的冲突及在统一场论内部的应用,为理解这一革命性理论提供清晰的逻辑框架。研究结果表明,“动量强守恒”作为统一场论的基础性公设,能够自洽地导出与狭义相对论形式相似的质速关系和质能方程,但其核心假设与主流物理学存在根本性对立。
关键词: 动量强守恒,张祥前统一场论,几何动量,能量强守恒,运动质量,静止质量,相对论
术语表
| 术语 | 解释 |
|---|---|
| 动量强守恒 | 统一场论中的核心公设,断言物体的总动量数量在所有惯性参考系中是绝对的、不随观察者运动状态而改变 |
| 几何动量 | 统一场论中引入的全新动量定义,表达式为 P ⃗ = m ( C ⃗ − V ⃗ ) \vec{P}=m(\vec{C}-\vec{V}) P=m(C−V),其中 C ⃗ \vec{C} C 为矢量光速 |
| 能量强守恒 | 统一场论中关于能量的公设,断言物体的总能量在所有惯性参考系中是绝对的、不随观察者运动状态而改变 |
| 运动质量 | 物体在运动状态下的质量,即相对论质量,表达式为 m = m ′ 1 − v 2 / c 2 m=\frac{m'}{\sqrt{1-v^2/c^2}} m=1−v2/c2m′ |
| 静止质量 | 物体相对观察者静止时的质量,即相对论中的静止质量 m ′ m' m′ |
| 矢量光速 | 统一场论中引入的概念, C ⃗ \vec{C} C 是空间本身的运动速度,其模长始终为常数 c c c |
1. “动量强守恒”的定义与核心公式
在张祥前提出的统一场论中,“动量强守恒”并非传统意义上对观察者相对性的妥协,而是对其进行了根本性的重塑。该理论的核心论断是:一个物体的总动量(以其数量大小衡量)在所有惯性参考系中是绝对的、不随观察者运动状态而改变的。 换言之,不同的观察者可能测量到的是同一物体动量的不同表现形式(例如,静止动量或运动动量),但其标量值在数量上必须保持恒等。
这一革命性的观点,通过一套精巧的公式体系得到体现:
1.1 动量定义公式:
统一场论引入了一个全新的动量定义,将其视为“几何动量”,并表示为:
P
⃗
=
m
(
C
⃗
−
V
⃗
)
\vec{P}=m(\vec{C}-\vec{V})
P=m(C−V)
其中:
- P ⃗ \vec{P} P 代表物体的总几何动量。
- m m m 是物体在运动状态下的质量,即“运动质量”。
- C ⃗ \vec{C} C 是矢量光速,其模长始终为常数 c c c。
- V ⃗ \vec{V} V 是物体相对于观察者的速度。
1.2 动量强守恒的数学表达:
“动量强守恒”的核心在于断言物体在任何状态下,其“静止动量”的数量与“运动动量”的数量恒等。这一关系被数学化为:
m
′
c
=
m
c
1
−
v
2
c
2
m'c=mc\sqrt{1-\frac{v^2}{c^2}}
m′c=mc1−c2v2
在此公式中:
- m ′ m' m′ 代表物体的“静止质量”(即当物体相对观察者速度为零时的质量)。
- m m m 代表物体以速度 v v v 运动时的“运动质量”。
公式的左侧 m ′ c m'c m′c,对应于物体静止时的动量大小。当 V ⃗ = 0 \vec{V}=0 V=0 时,根据动量定义公式, P ⃗ 静 = m ′ C ′ ⃗ \vec{P}_{\text{静}}=m'\vec{C'} P静=m′C′ (这里的 C ′ ⃗ \vec{C'} C′ 是物体静止时与其相对的空间运动速度),其模长即为 m ′ c m'c m′c。
公式的右侧 m c 1 − v 2 / c 2 mc\sqrt{1-v^2/c^2} mc1−v2/c2,则代表了物体运动时的动量大小。通过几何推导,得出 ∣ C ⃗ − V ⃗ ∣ = c 1 − v 2 / c 2 |\vec{C}-\vec{V}|=c\sqrt{1-v^2/c^2} ∣C−V∣=c1−v2/c2。因此, P ⃗ 动 = m ( C ⃗ − V ⃗ ) \vec{P}_{\text{动}}=m(\vec{C}-\vec{V}) P动=m(C−V) 的模长为 m × c 1 − v 2 / c 2 m\times c\sqrt{1-v^2/c^2} m×c1−v2/c2。
图2展示了动量强守恒的几何关系,通过矢量三角形直观地展示了 C ⃗ \vec{C} C、 V ⃗ \vec{V} V 和 C ⃗ − V ⃗ \vec{C}-\vec{V} C−V 之间的关系:
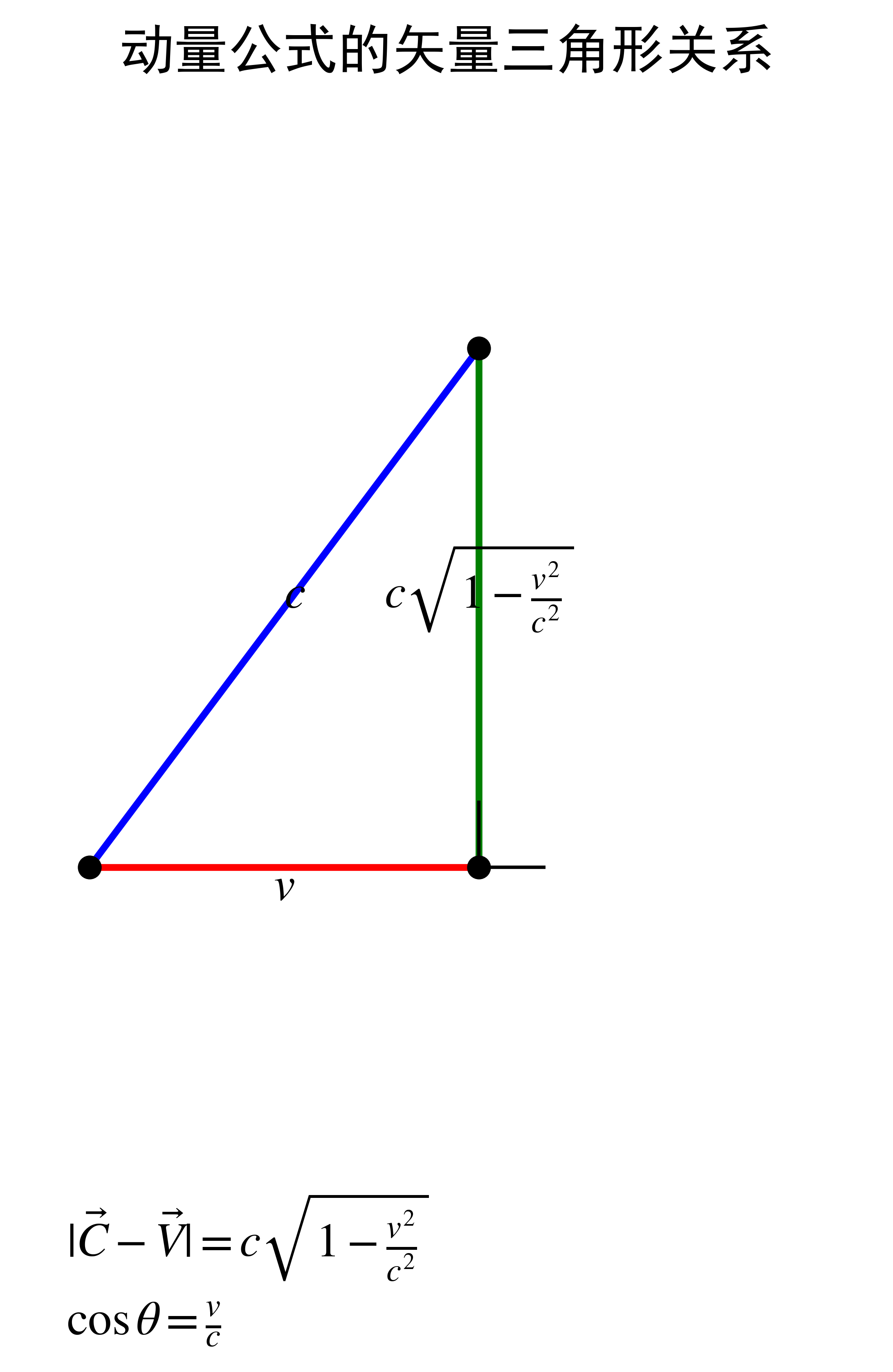
该等式最关键的断言是:静止动量的标量值( m ′ c m'c m′c)必然等于运动动量的标量值( m c 1 − v 2 / c 2 mc\sqrt{1-v^2/c^2} mc1−v2/c2)。
2. “为什么”动量强守恒?——理论公设与推导
“动量强守恒”并非源于对现有实验数据的归纳,而是统一场论的基本公设(axioms)和逻辑基石之一。其理论依据和推导路径,可以概括为以下几点:
2.1 第一性原理(公设):
统一场论的一个根本性假设是:宇宙中任何静止的物体,其周围的空间都处于一种以光速 C ⃗ \vec{C} C 向外发散的运动状态。这意味着,即使一个宏观物体在某个参考系中表现为“静止”,它也必然携带着一个内禀的、由其与时空相互作用产生的“静止动量”,其形式为 m ′ C ⃗ m'\vec{C} m′C。
2.2 观察者原理:
《统一场论》明确指出:“观察者只能观察运动状态,而不能改变、决定运动状态。” 这一原则强调了物体的运动状态及其携带的总动量是客观存在且绝对的实体。任何观察者,无论其自身的运动状态如何,都只是从不同的视角去“测量”这个客观存在的动量。因此,不同观察者测量到的动量总量,理论上应当是相同的。
2.3 导出相对论关系:
将“动量强守恒”的核心公式
m
′
c
=
m
c
1
−
v
2
/
c
2
m'c=mc\sqrt{1-v^2/c^2}
m′c=mc1−v2/c2,两边同时除以标量光速
c
c
c,我们立即得到:
m
′
=
m
1
−
v
2
c
2
或等价地
m
=
m
′
1
−
v
2
/
c
2
m'=m\sqrt{1-\frac{v^2}{c^2}}\quad\text{或等价地}\quad m=\frac{m'}{\sqrt{1-v^2/c^2}}
m′=m1−c2v2或等价地m=1−v2/c2m′
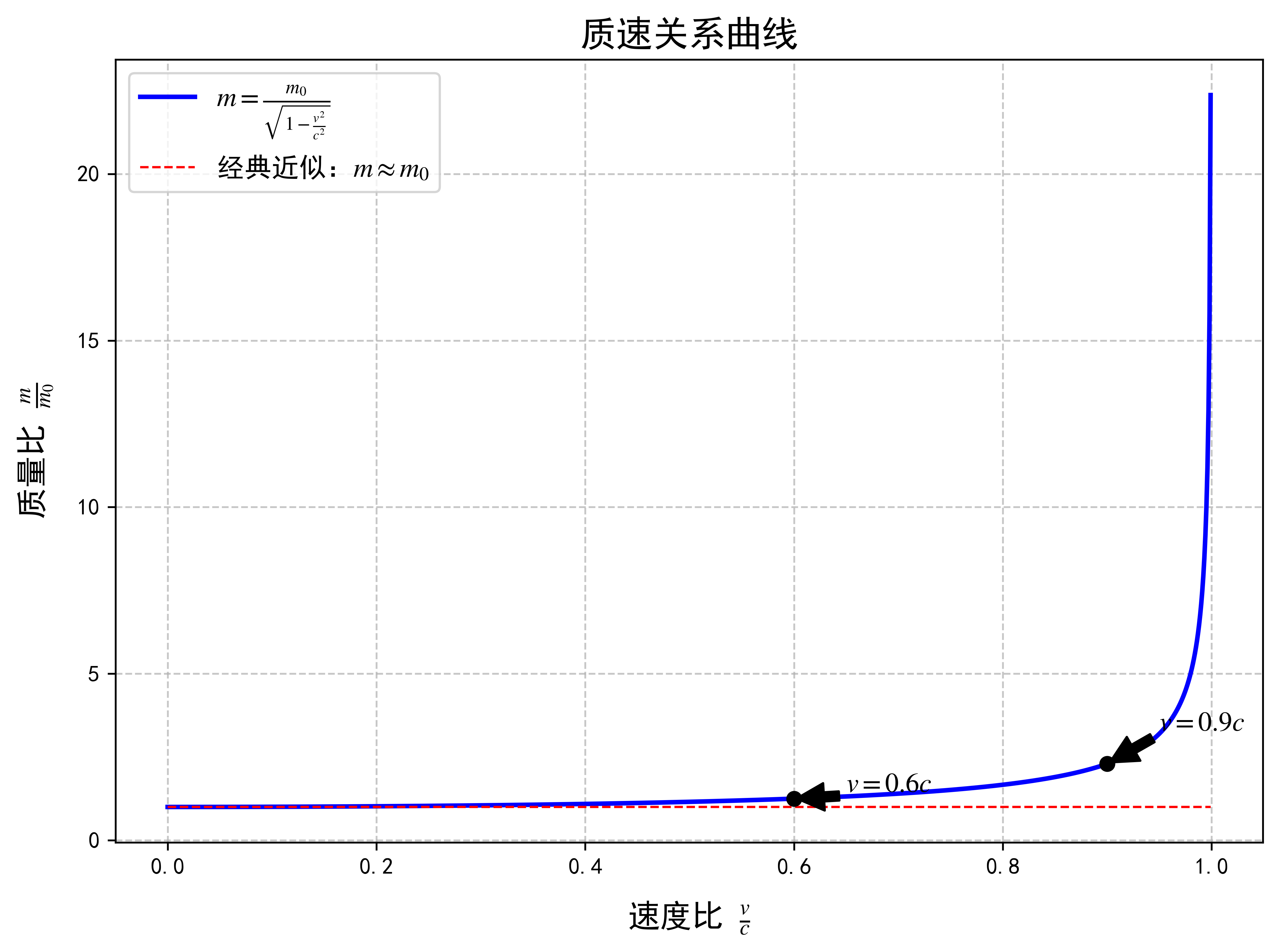
这正是狭义相对论中著名的“质速关系”公式。统一场论将这一公式视为“动量强守恒”这一公设的必然推论,而非一个独立或需要额外验证的假设。
图3展示了质速关系曲线,直观地显示了运动质量随速度变化的关系:
2.4 导出能量强守恒:
进一步,将上述质速关系公式
m
′
=
m
1
−
v
2
/
c
2
m'=m\sqrt{1-v^2/c^2}
m′=m1−v2/c2 的两边同时乘以
c
2
c^2
c2,我们便得到了能量方程:
E
=
m
′
c
2
=
m
c
2
1
−
v
2
c
2
E=m'c^2=mc^2\sqrt{1-\frac{v^2}{c^2}}
E=m′c2=mc21−c2v2
这意味着,统一场论认为物体的总能量
E
E
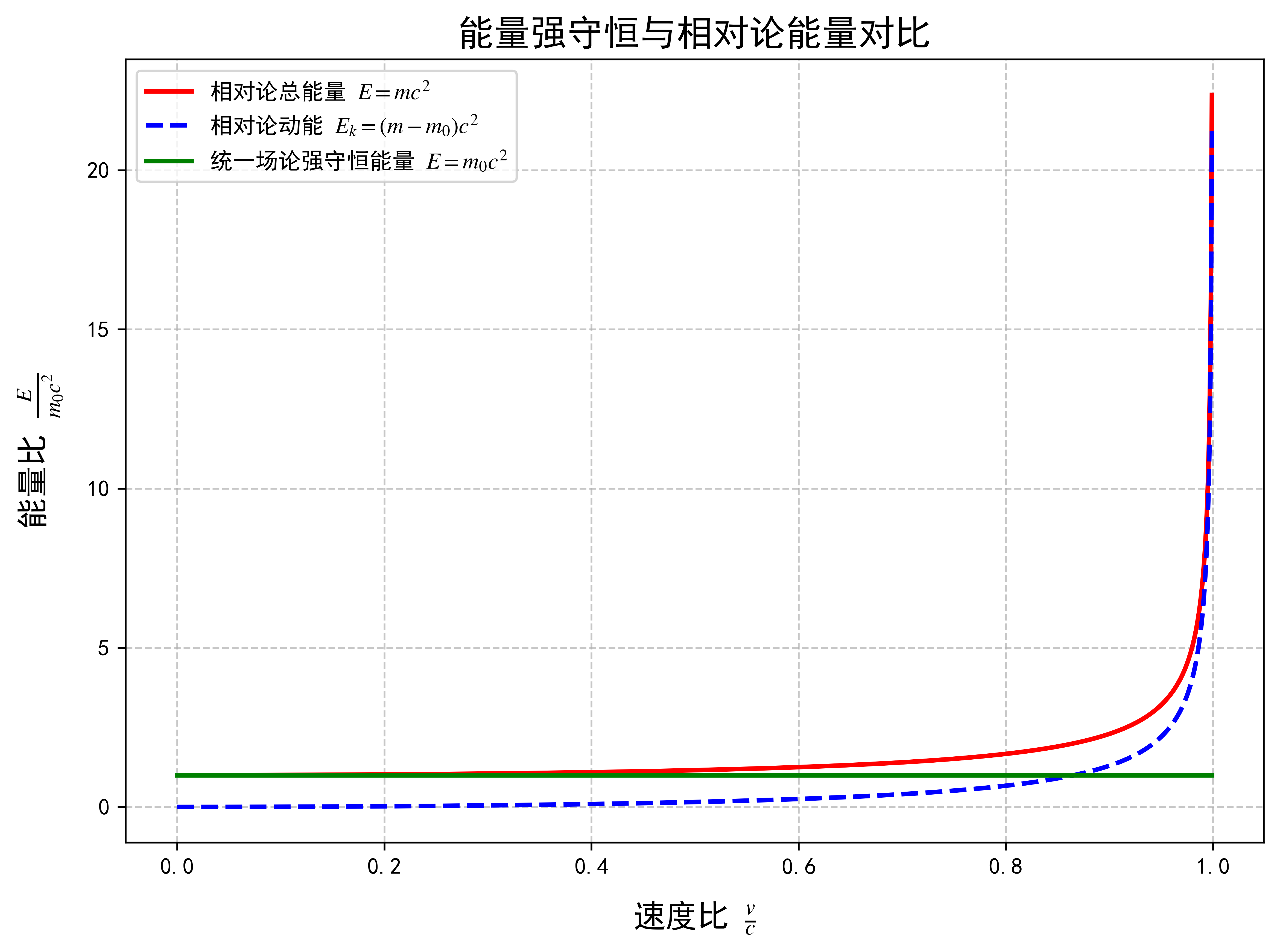
E 同样是一个与观察者无关的绝对常量,即“能量强守恒”。这一点与主流狭义相对论中“运动物体能量更大”的观点存在根本性冲突。统一场论认为,主流观点将能量的“表现形式”误读为能量的“总量”增加了。
图5对比了能量强守恒与相对论能量的关系,直观展示了两者的差异:
3. 数值分析验证
为了展示统一场论内部的数学自洽性,我们将通过具体的数值计算,来验证“动量强守恒”公式的有效性。需要强调的是,此处进行的数值分析,是在完全接受并遵循该理论公设的前提下,展示其数学推导的逻辑一致性,而非提供独立的、脱离理论框架的实验证据。
3.1 设定参数:
- 光速 c = 3.00 × 1 0 8 m/s c=3.00\times10^8\,\text{m/s} c=3.00×108m/s
- 物体静止质量 m ′ = 1.00 kg m'=1.00\,\text{kg} m′=1.00kg
- 物体运动速度 v = 0.60 c = 1.80 × 1 0 8 m/s v=0.60c=1.80\times10^8\,\text{m/s} v=0.60c=1.80×108m/s (即 v / c = 0.6 v/c=0.6 v/c=0.6)
3.2 验证步骤:
步骤一:计算静止动量大小
根据动量强守恒的定义,静止动量的大小为:
KaTeX parse error: Undefined control sequence: \cdotp at position 1: \̲c̲d̲o̲t̲p̲
根据“动量强守恒”的公设,运动状态下的动量大小也应等于此值。
步骤二:计算运动质量
m
m
m
利用由动量强守恒推导出的质速关系:
m
=
m
′
1
−
v
2
/
c
2
=
1.00
kg
1
−
(
0.60
)
2
=
1.00
kg
1
−
0.36
=
1.00
kg
0.64
=
1.00
kg
0.8
=
1.25
kg
m=\frac{m'}{\sqrt{1-v^2/c^2}}=\frac{1.00\,\text{kg}}{\sqrt{1-(0.60)^2}}=\frac{1.00\,\text{kg}}{\sqrt{1-0.36}}=\frac{1.00\,\text{kg}}{\sqrt{0.64}}=\frac{1.00\,\text{kg}}{0.8}=1.25\,\text{kg}
m=1−v2/c2m′=1−(0.60)21.00kg=1−0.361.00kg=0.641.00kg=0.81.00kg=1.25kg
可见,运动质量
m
m
m(1.25 kg)大于静止质量
m
′
m'
m′(1.00 kg),符合理论预测。
步骤三:计算运动动量大小
∣
P
⃗
动
∣
|\vec{P}_{\text{动}}|
∣P动∣
根据统一场论的动量定义
P
⃗
动
=
m
(
C
⃗
−
V
⃗
)
\vec{P}_{\text{动}}=m(\vec{C}-\vec{V})
P动=m(C−V),其大小计算需要考虑
C
⃗
\vec{C}
C 和
V
⃗
\vec{V}
V 之间的几何关系。推导出
C
⃗
\vec{C}
C 与
V
⃗
\vec{V}
V 之间的夹角
θ
\theta
θ 满足
cos
θ
=
v
/
c
\cos\theta=v/c
cosθ=v/c。
利用余弦定理,向量
C
⃗
−
V
⃗
\vec{C}-\vec{V}
C−V 的模长为:
∣
C
⃗
−
V
⃗
∣
=
∣
C
⃗
∣
2
+
∣
V
⃗
∣
2
−
2
∣
C
⃗
∣
∣
V
⃗
∣
cos
θ
|\vec{C}-\vec{V}|=\sqrt{|\vec{C}|^2+|\vec{V}|^2-2|\vec{C}||\vec{V}|\cos\theta}
∣C−V∣=∣C∣2+∣V∣2−2∣C∣∣V∣cosθ
将
∣
C
⃗
∣
=
c
|\vec{C}|=c
∣C∣=c 和
∣
V
⃗
∣
=
v
|\vec{V}|=v
∣V∣=v 代入,并使用
cos
θ
=
v
/
c
\cos\theta=v/c
cosθ=v/c:
∣
C
⃗
−
V
⃗
∣
=
c
2
+
v
2
−
2
c
v
(
v
/
c
)
=
c
2
+
v
2
−
2
v
2
=
c
2
−
v
2
|\vec{C}-\vec{V}|=\sqrt{c^2+v^2-2cv(v/c)}=\sqrt{c^2+v^2-2v^2}=\sqrt{c^2-v^2}
∣C−V∣=c2+v2−2cv(v/c)=c2+v2−2v2=c2−v2
∣
C
⃗
−
V
⃗
∣
=
c
2
(
1
−
v
2
/
c
2
)
=
c
1
−
v
2
/
c
2
|\vec{C}-\vec{V}|=\sqrt{c^2(1-v^2/c^2)}=c\sqrt{1-v^2/c^2}
∣C−V∣=c2(1−v2/c2)=c1−v2/c2
代入数值:
∣
C
⃗
−
V
⃗
∣
=
(
3.00
×
1
0
8
m/s
)
×
1
−
(
0.60
)
2
=
(
3.00
×
1
0
8
m/s
)
×
0.8
=
2.40
×
1
0
8
m/s
|\vec{C}-\vec{V}|=(3.00\times10^8\,\text{m/s})\times\sqrt{1-(0.60)^2}=(3.00\times10^8\,\text{m/s})\times0.8=2.40\times10^8\,\text{m/s}
∣C−V∣=(3.00×108m/s)×1−(0.60)2=(3.00×108m/s)×0.8=2.40×108m/s
现在,计算运动动量的大小:
KaTeX parse error: Undefined control sequence: \cdotp at position 1: \̲c̲d̲o̲t̲p̲
步骤四:验证守恒
通过计算,我们得到:
- 静止动量大小 KaTeX parse error: Undefined control sequence: \cdotp at position 1: \̲c̲d̲o̲t̲p̲
- 运动动量大小 KaTeX parse error: Undefined control sequence: \cdotp at position 1: \̲c̲d̲o̲t̲p̲
数值分析结论:
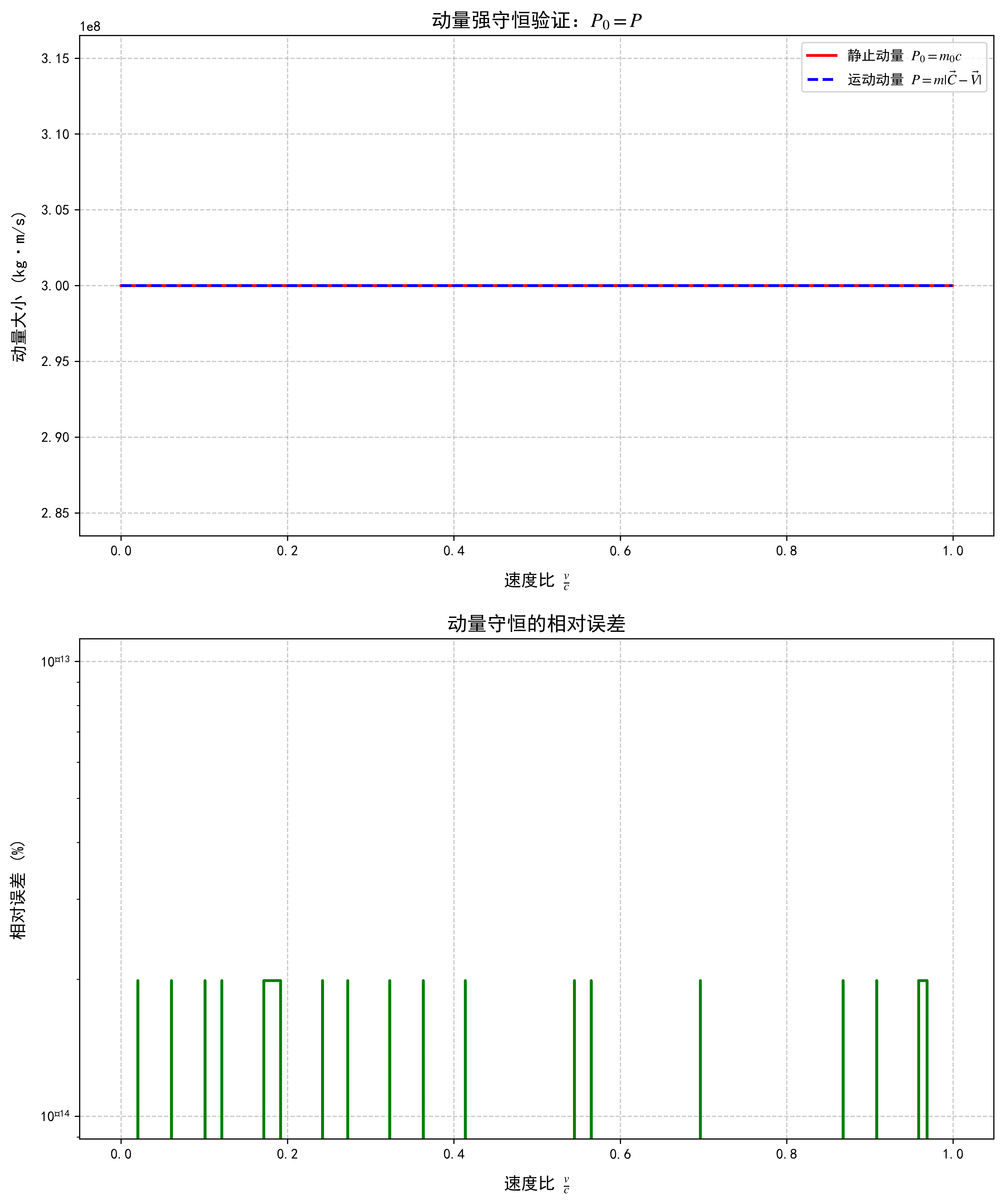
该数值计算结果表明,在设定的速度下,
P
静
P_{\text{静}}
P静 和
∣
P
⃗
动
∣
|\vec{P}_{\text{动}}|
∣P动∣ 的大小是严格相等的。这清晰地展示了统一场论内部的数学自洽性:一旦接受“动量数量与观察者无关”这一强守恒的公设,整套数学框架就能无矛盾地推导出与狭义相对论形式一致的运动学关系。 运动质量的增加,恰好补偿了
∣
C
⃗
−
V
⃗
∣
|\vec{C}-\vec{V}|
∣C−V∣ 的减小,从而保证了总动量数量的绝对不变。
图4展示了不同速度下静止动量与运动动量的关系,进一步验证了动量强守恒的普遍适用性:
4. 与主流理论的冲突及理论内部应用
4.1 与狭义相对论的根本冲突:
“动量强守恒”的基石地位,使其与主流物理学,特别是狭义相对论,在最根本的原则上存在直接的、不可调和的冲突。主流物理学认为动量和能量是观察者相对的物理量,它们的大小会随着观察者参考系的运动状态而变化。然而,统一场论的“强守恒”理念则坚信这些物理量是绝对的、客观的。
大型强子对撞机(LHC)中粒子能量随速度急剧增加的实验现象。在主流观点看来,这是对相对论能量-动量关系的有力支持。而统一场论对此的解释是:这些高能粒子所表现出的巨大能量,实际上是其固有能量 m ′ c 2 m'c^2 m′c2 在不同观察条件下的“表现形式”,其绝对总量并未发生增加。这种对能量增加的解释,是统一场论区别于相对论的关键之一。
4.2 理论内部的应用:
“动量强守恒”不仅是理论基石,更是解释一些前沿设想的核心机制。例如,在关于“加质量运动”和“光速飞行”的探讨中,该公设扮演着至关重要的角色。
《揭秘外星人的飞碟之谜》等著作暗示,如果能够通过某种“人工场扫描”技术,使得物体的静止质量 m ′ m' m′ 趋近于零( m ′ → 0 m'\to0 m′→0)。那么,根据动量强守恒公式 m ′ c = m c 1 − v 2 / c 2 m'c=mc\sqrt{1-v^2/c^2} m′c=mc1−v2/c2,为了避免运动质量 m m m 趋于无穷大(这在物理上是不可能的),唯一可能的数学结论是分母 1 − v 2 / c 2 \sqrt{1-v^2/c^2} 1−v2/c2 必须趋近于零,即要求物体的运动速度 v v v 趋近于光速 c c c( v → c v\to c v→c)。因此,“动量强守恒”理论为“质量归零则必达光速”的“飞碟”或超光速飞行原理,提供了强有力的理论依据。
结论
张祥前统一场论中的“动量强守恒”是一个foundational 的公设,它主张动量的数值是绝对的,不随观察者而变化。这一核心理念,通过引入独特的动量定义和严格的数学推导,能够自洽地导出与狭义相对论形式上相似的质速关系和质能方程。数值分析也证实了该理论在内部逻辑上的高度一致性。
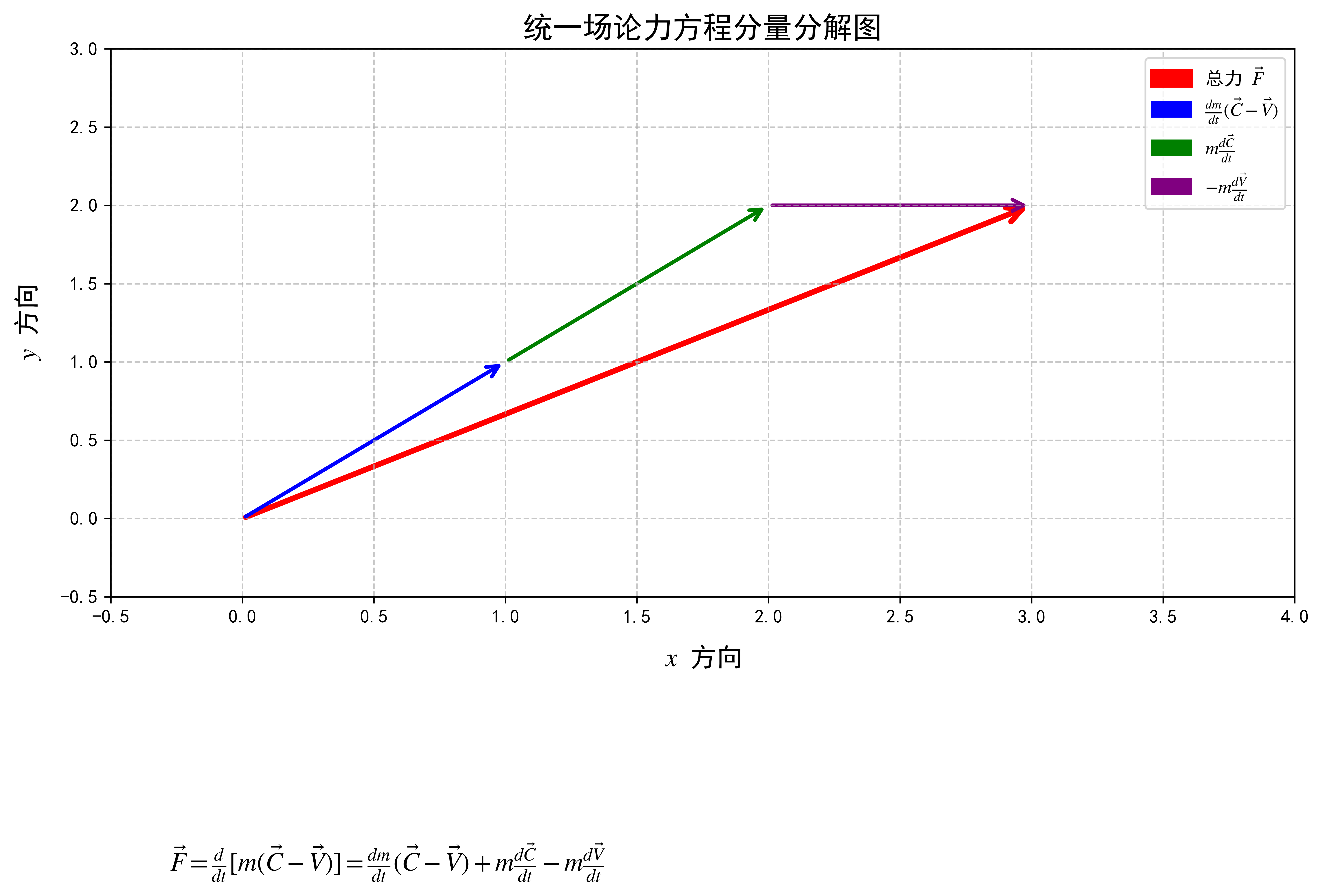
统一场论的力方程是动量强守恒理论的直接应用,它将力分解为三个分量:
F ⃗ = d m d t ( C ⃗ − V ⃗ ) + m d C ⃗ d t − m d V ⃗ d t \vec{F}=\frac{dm}{dt}(\vec{C}-\vec{V})+m\frac{d\vec{C}}{dt}-m\frac{d\vec{V}}{dt} F=dtdm(C−V)+mdtdC−mdtdV
图6展示了力方程的分量分解关系,直观地反映了统一场论中力的构成:
然而,该理论的核心公设——“动量强守恒”——与已被大量实验证据支持的狭义相对论在基本原理上存在根本性对立。这构成了张祥前统一场论目前面临的主要争议和最严峻的理论挑战。尽管如此,“动量强守恒”作为统一场论的基石,不仅重塑了对动量、能量的理解,也为探索超光速飞行等前沿科学问题提供了独特的理论视角。
参考文献:
- 张祥前. 《统一场论》. 2024

























 277
277

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










