震惊！Python递归竟然可以加速

• 众所周知，递归算法因其代码简短，易于理解，深受大家的喜爱。但我们也知道，递归算法其实是非常消耗内存和时间的，尤其是在算法求解问题规模稍稍大一些之后，表现得更为明显。因此，我们在对递归算法进行优化时，往往会考虑加入备忘机制，避免反复计算，但在python标准库中其实已经为我们内置了提供该功能的函数，我们来了解一下吧~

  计算Fibonacci数递归算法代码及运行截图如下：

  import time
  
  def fibonacci(n):
      if n < 2:
          return n
      return fibonacci(n-1) + fibonacci(n-2)
  
  if __name__ == '__main__':
      t0 = time.perf_counter()
      print(fibonacci(40))
      print(time.perf_counter() - t0)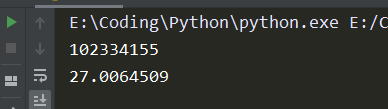
  

  
  我们可以看到，仅仅运行40时，时间已经达到了27s之多，这是由于递归的特性导致，我们再来看下引入备忘机制之后的表现吧~

  import time
  import functools #引入functools包
  
  @functools.lru_cache() # 在fibonacci函数上加上装饰器函数functools.lru_cache()
  def fibonacci(n):
      if n < 2:
          return n
      return fibonacci(n-1) + fibonacci(n-2)
  
  if __name__ == '__main__':
      t0 = time.perf_counter()
      print(fibonacci(40))
      print(time.perf_counter() - t0)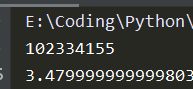
  

  
  运行时间缩短到3.4s，可以看到，提升还是比较明显的。

  lru_cache函数可以使用两个可选的参数来配置。它的签名是：

  functools.lru_cache(maxsize=128, typed=False)
  

  maxsize指定存储多少个调用的结果。缓存满了之后，旧的结果会被扔掉，腾出空间。为了得到最佳的性能，maxsize应该设为2的幂。typed参数如果设置为True，把不同的参数类型得到的结果分开保存，即把通常认为相等的浮点数和整型参数（如1和1.0）区分开。
  同时，因为lru_cache使用字典存储结果，而且键根据调用时传入的定位参数和关键字参数创建，所以被lru_cache装饰的函数，它的所有的参数都是可散列的。具体python怎么划分可散列对象可自行百度。