8.12 8.13

 

8.12

(a) 三个符号的信源存在几种不同的Huffman编码?

(b) 构造出这些编码.

 

解答

(a)    两种

(b)    [0 10 11] 和 [1 00 01]

 

8.13

(a)计算下表所示信源的熵.

rk	P(rk)	Code2	l2(rk)
0	0.19	11	2
1/7	0.25	01	2
2/7	0.21	10	2
3/7	0.16	001	3
4/7	0.08	0001	4
5/7	0.06	00001	5
6/7	0.03	000001	6
1	0.02	000000	6

(b)构造Huffman编码, 并与表中的Code2比较.

(c)构造B1编码

(d)构造2bit的二进制偏移编码

(e)将符号分成两组, 构造Huffman偏移编码

(f)计算这些编码的平均字长并与(a)中计算的熵比较.

解答

(a)

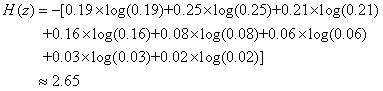
(b) Huffman

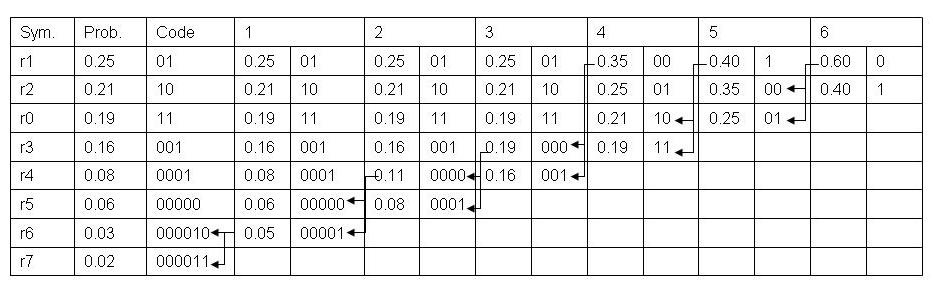
所构造的Huffman编码和Code2的编码长度一致.

 

(c) B1编码

	r1	r2	r0	r3	r4	r5	r6	r7
Code	C0	C1	C0 C0	C0 C1	C1 C0	C1 C1	C0 C0 C0	C0 C0 C1

 

(d) 二进制偏移编码

设11为偏移码

	r1	r2	r0	r3	r4	r5	r6	r7
Code	00	01	10	11 00	11 01	11 10	11 11 00	11 11 01

 

(e) Huffman偏移编码

	Sym.	Prob.		Huffman Shift
Block 1	r1	.25		00
	r2	.21		10
	r0	.19		000
	r3	.16		001
Block 2	r4	.08	.19	11 1
	r5	.06		11 00
	r6	.03		11 010
	r7	0.2		11 011

 

(f)

熵	2.65
Huffman	2.7
B1	3.18
偏移编码	2.8
Huffman偏移编码	2.7