1、双指针
算法讲解
基础算法之一,也是笔试中比较常考的一个算法,双指针题型以及变型有很多,这里面主要列举两大类,一类是在两个数组中使用两个指针分别指向这两个数组,这一类问题中,最经典的就是判断子序列的问题,另一类则是在一个数组中使用两个指针指向这一个数组,这类问题又称为同向双指针问题,也称为滑动窗口问题,这类问题的本质其实可以理解为动态规划,比如l和r两个双指针,很多问题其实就变为以r结尾的最大值/最小值,这类问题是需要满足单调性的:当[l,r]区间不满足条件时,l指针需要左移,直到[l,r]区间满足条件为止,且当l=r时,都可以满足条件,很多时候,如果数组的数值可以取负数,是不能使用双指针来求最优解的,就是因为不满足单调性,这种题目其实比较难的是一种抽象问题的能力,有的题目需要把问题做一个转化,首先需要判断是否满足单调性,如果满足,就需要把问题转化为一个可以使用双指针去解决的一个滑动窗口问题。
1.1 多指针滑动窗口
这类题型一般是有多个数组或者字符串,然后多个指针指向不同的数组或者字符串,这类题型最经典的问题就是判断子序列问题,很多题目都可以抽象成这样一个问题。
class Solution {
public int minSwaps(int[] nums) {
int k=0,n=nums.length;
for(int i=0;i<n;++i){
if(nums[i]==1){
k++;
}
}
if(n<=1){
return 0;
}
int l=0;
int max=Integer.MAX_VALUE;
int ans=0;
int[] newNums=new int[n+k-1];
for(int i=0;i<newNums.length;++i){
newNums[i]=nums[i%n];
}
for(int r=0;r<newNums.length;++r){
if(newNums[r]==0){
ans++;
}
while(r-l+1>k){
if(newNums[l]==0){
ans--;
}
l++;
}
if(r-l+1==k){
max=Math.min(max,ans);
}
}
return max;
}
}
class Solution {
public int matchPlayersAndTrainers(int[] players, int[] trainers) {
int n=players.length,m=trainers.length;
int left=0,right=0;
Arrays.sort(players);
Arrays.sort(trainers);
int ans=0;
while(left<n&&right<m){
if(players[left]<=trainers[right]){
ans++;
left++;
}
right++;
}
return ans;
}
}
import java.util.*;
import java.io.*;
public class Main{
public static void main (String[] args) {
Scanner sc=new Scanner(System.in);
int q=sc.nextInt();
for(int i=0;i<q;++i){
String s=sc.next();
String t=sc.next();
if(transfor(s, t)){
System.out.println("Yes");
}else{
System.out.println("No");
}
}
}
public static boolean transfor(String s,String t){
int n=s.length(),m=t.length();
int left=0,right=0;
if((n-m)%3!=0){
return false;
}else if(n==m){
if(s.equals(t)){
return true;
}else{
return false;
}
}else{
String res;
if(n>m){
res=find(s, t);
}else{
res=find(t, s);
}
return check(res);
}
}
public static String find(String s,String t){
String res="";
int n=s.length(),m=t.length();
int l=0,r=0;
while(l<n){
if(r<m&&s.charAt(l)==t.charAt(r)){
l++;
r++;
}else{
res+=s.charAt(l++);
}
}
return res;
}
public static boolean check(String str){
int n=str.length();
if(n%3!=0) return false;
for(int i=0;i<n;i+=3){
if(!str.substring(i,i+3).equals("mhy")){
return false;
}
}
return true;
}
}
1.2定长滑动窗口
这一类题型中,滑动窗口的大小是固定的,一般题目都会被描述为求一个长度为k的子数组/子串的最大/最小值。因此,这种题目的难度不高,直接使用同向双指针的方式枚举两个指针l和r即可,其中r=l+k-1
class Solution {
public int maxVowels(String s, int k) {
int n=s.length();
if(n==0){
return 0;
}
Set<Character> set=new HashSet<>();
set.add('a');
set.add('e');
set.add('i');
set.add('o');
set.add('u');
int ans=0;
for(int i=0;i<k&&i<n;++i){
if(set.contains(s.charAt(i))){
ans++;
}
}
if(n<=k){
return ans;
}
int max=ans;
int left=0;
for(int i=k;i<n;i++){
if(set.contains(s.charAt(i))){
ans++;
}
if(set.contains(s.charAt(left))){
ans--;
}
left++;
max=Math.max(ans,max);
}
return max;
}
}
class Solution {
public long maxSum(List<Integer> nums, int m, int k) {
HashMap<Integer,Integer> map=new HashMap<>();
int l=0;
long max=0;
long ans=0;
int n=nums.size();
for(int r=0;r<n;r++){
int num=nums.get(r);
map.put(num,map.getOrDefault(num,0)+1);
ans+=(long)num;
while(r-l+1>k){
int leftNum=nums.get(l);
map.put(leftNum,map.get(leftNum)-1);
if (map.get(leftNum) == 0) {
map.remove(leftNum);
}
ans-=(long)leftNum;
l++;
}
if(r-l+1==k&&map.size()>=m){
max=Math.max(max,ans);
}
}
return max;
}
}
import java.util.*;
public class Main{
public static void main (String[] args) {
Scanner sc=new Scanner(System.in);
int n=sc.nextInt();
int k=sc.nextInt();
int[] nums=new int[n];
for(int i=0;i<n;++i){
nums[i]=sc.nextInt();
}
int res=Integer.MAX_VALUE;
for(int x=0;x<=9;x++){
int cost=0;
for(int l=0,r=0;r<n;++r){
cost+=Math.abs(nums[r]-x);
while(r-l+1>k){
cost-=Math.abs(nums[l]-x);
l++;
}
if(r-l+1==k){
res=Math.min(res,cost);
}
}
}
System.out.println(res);
}
}
LeetCode 2134. 最少交换次数来组合所有的 1 II
class Solution {
public int minSwaps(int[] nums) {
int k=0,n=nums.length;
for(int i=0;i<n;++i){
if(nums[i]==1){
k++;
}
}
if(n<=1){
return 0;
}
int l=0;
int max=Integer.MAX_VALUE;
int ans=0;
int[] newNums=new int[n+k-1];
for(int i=0;i<newNums.length;++i){
newNums[i]=nums[i%n];
}
for(int r=0;r<newNums.length;++r){
if(newNums[r]==0){
ans++;
}
while(r-l+1>k){
if(newNums[l]==0){
ans--;
}
l++;
}
if(r-l+1==k){
max=Math.min(max,ans);
}
}
return max;
}
}
1.3不定长滑动窗口
这一类题目,滑动窗口的大小是不固定的,一般需要利用单调性去求最大/最小值 或者最长/最短的子串/子序列。这种题目,很多可以使用双指针(一般都是同向双指针)求解的,也可以使用前缀和+哈希表来求解,而且前缀和+哈希表这种方法,即使不满足单调性,比如数组的数值为负数,也是可以求解的。
LeetCode 1493. 删掉一个元素以后全为 1 的最长子数组
class Solution {
public int longestSubarray(int[] nums) {
int n=nums.length;
int l=0,ans=-1,max=0;
for(int r=0;r<n;++r){
if(nums[r]==1){
continue;
}else if(nums[r]==0){
if(ans==-1){
ans=r;
}else{
max=Math.max(max,r-l-1);
l=ans+1;
ans=r;
}
}
}
max=Math.max(max,n-l-1);
return max;
}
}
class Solution {
public int totalFruit(int[] fruits) {
int l=0,n=fruits.length,result=0;
Map<Integer,Integer> map=new HashMap<>();
for(int r=0;r<n;++r){
map.put(fruits[r],map.getOrDefault(fruits[r],0)+1);
while(map.size()>2){
map.put(fruits[l],map.get(fruits[l])-1);
if(map.get(fruits[l])==0){
map.remove(fruits[l]);
}
++l;
}
result=Math.max(result,r-l+1);
}
return result;
}
}
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
solve(scanner);
}
public static void solve(Scanner scanner) {
int n = scanner.nextInt();
int k = scanner.nextInt();
int[] w = new int[n];
for (int i = 0; i < n; i++) {
w[i] = scanner.nextInt();
}
long res = 0;
Map<Integer, Integer> cnts = new HashMap<>();
int l = 0;
for (int r = 0; r < n; r++) {
cnts.put(w[r], cnts.getOrDefault(w[r], 0) + 1);
while (cnts.get(w[r]) >= k) {
res += n - r;
cnts.put(w[l], cnts.get(w[l]) - 1);
l++;
}
}
System.out.println(res);
}
}
import java.util.*;
public class Main{
public static void main (String[] args) {
Scanner sc=new Scanner(System.in);
int n=sc.nextInt();
long[] nums=new long[n];
for(int i=0;i<n;++i){
nums[i]=sc.nextLong();
}
Arrays.sort(nums);
int l=0,res=Integer.MAX_VALUE;
for(int r=0;r<n;++r){
while(nums[r]-nums[l]+1>n){
l++;
}
res=Math.min(res,n-(r-l+1));
}
System.out.println(res);
}
}
2、前缀和
算法讲解
前缀和算法,是用来快速求解数组中某一个区间的区间和的值,如果对于每一个询问,都可以在O(1)的时间复杂度内快速求解,如果使用枚举的思想,则平均复杂度为O(n),远高于O(1)的复杂度,那么前缀和是如何做到这一点的,其实是通过区间拆分+预处理的思想得到的,预处理的复杂度为O(n)
算法步骤
对于给定的一个数组,如下图所示,其中,0~8为数组的下标
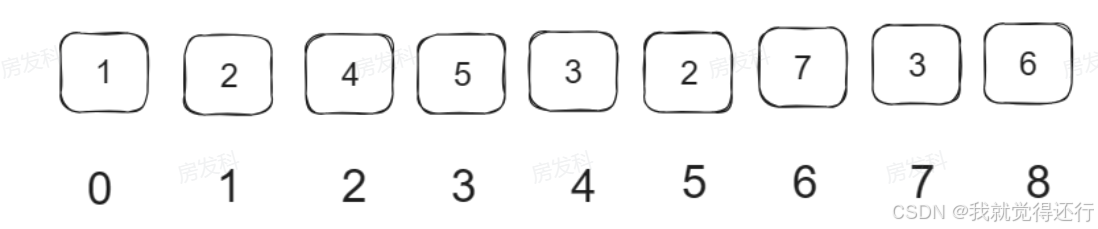
那么,对于数组任意的一个区间范围[i,j],如何快速地求解它的区间和?
首先,我们可以看几个例子
[0,2]的区间和为w[0]+w[1]+w[2]=1+2+4=7
[1,3]的区间和为w[1]+w[2]+w[3]=2+4+5=11
我们可以预处理一个前缀和数组s,其中s[i]表示区间[0,i]的区间和,那么我们很容易得出s[i]的递推式s[i]=s[i-1]+w[i],s[0]=w[0]
对于区间[0,i]的前缀和为s[i],区间[0,j]的前缀和为s[j],则区间[j,i]的前缀和为s[i]-s[j-1]
因此,我们只需要预处理出前缀和数组,就可以根据上述计算公式,快速地计算出任意一个区间的区间和,在实际笔试或者面试中,为了减少边界情况的考虑,我们更习惯性地将数组下标设置为从1开始。
使用场景
- 一维前缀和主要是用于快速地求解某一个区间和,但是前缀和是静态的算法,就是说这个数组中每一个元素的值不能被修改,如果要一边修改一边动态查询,就需要使用树状数组或者线段树这种数据结构来实现动态查询。
- 二维前缀和主要是针对二维场景,比如对于一个矩阵,矩阵的长度为
n,宽度为m,它对应有n*m个整数点,每一个点对应的权值不同,使用二维前缀和可以快速求出起点为(x1,y1),终点为(x2,y2)的小矩形的权值和。
一般会结合哈希表,动态规划,贪心等算法考察
1.1朴素前缀和
基本上直接使用一维前缀和或者二维前缀和的模板,即可 ac。
class NumMatrix {
private int[][] matrix;
private int[][] matrixSum;
public NumMatrix(int[][] matrix) {
this.matrix=matrix;
int n=matrix.length,m=matrix[0].length;
matrixSum=new int[n+1][m+1];
for(int i=1;i<=n;i++){
for(int j=1;j<=m;++j){
matrixSum[i][j]=matrixSum[i][j-1]+matrixSum[i-1][j]-matrixSum[i-1][j-1]+matrix[i-1][j-1];
}
}
}
public int sumRegion(int row1, int col1, int row2, int col2) {
row1++;
col1++;
row2++;
col2++;
return matrixSum[row2][col2]-matrixSum[row2][col1-1]-matrixSum[row1-1][col2]+matrixSum[row1-1][col1-1];
}
}
import java.util.*;
public class Main{
public static void main (String[] args) {
Scanner sc=new Scanner(System.in);
//敌人数
int n=sc.nextInt();
//横坐标参数A 即行差值
int a=sc.nextInt();
//纵坐标参数B 即列差值
int b=sc.nextInt();
int N = 1010;
int[][] s = new int[N][N];
for(int i=0;i<n;++i){
int x=sc.nextInt();
int y=sc.nextInt();
s[x][y]++;
}
//二维前缀和
for (int i = 1; i < 1010; i++) {
for (int j = 1; j < 1010; j++) {
s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
}
}
int res=0;
// 枚举矩形的右下角的横坐标
for(int x2=a+1;x2<1010;x2++){
// 枚举矩形右下角的纵坐标
for(int y2=b+1;y2<1010;y2++){
int x1=x2-a,y1=y2-b;// 矩形左上角的横纵坐标
// 求横坐标在[x1,x2] 纵坐标在[y1,y2]的元素个数
int cnt=s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1];
res=Math.max(res,cnt);
}
}
System.out.println(res);
}
}
塔子哥划分
有一定难度,其实就是求一个靠近sum/2的数,这个数是由正方形中的数的和组成的,那么可以考虑枚举正方形的左上角端点,然后二分正方形的边长,找到一个正方形数之和大于等于sum/2的最小边长。需要快速求出一个正方形内数的和,可以通过预处理二维前缀和
import java.util.*;
import java.io.*;
public class Main{
static int[][] g;
public static void main (String[] args) {
Scanner sc=new Scanner(System.in);
int n=sc.nextInt();
int m=sc.nextInt();
g=new int[n+1][m+1];
for(int i=1;i<=n;++i){
for(int j=1;j<=m;++j){
g[i][j]=sc.nextInt();
}
}
//计算前缀和
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
g[i][j] += g[i-1][j] + g[i][j-1] - g[i-1][j-1];
}
}
long sum = g[n][m];
long target=(sum+1)/2;
long ans=sum;
//二分查找
for(int i=1;i<=n;++i){
for(int j=1;j<=m;++j){
int l=1,r=Math.min(n - i + 1, m - j + 1);
while(l<r){
int mid=l + ((r - l) >> 1 );
if(get(i,j,i+mid-1,j+mid-1)>=target){
r=mid;
}else{
l=mid+1;
}
}
ans = Math.min(ans, myabs(sum - 2 * get(i, j, i + l - 1, j + l - 1)));
if (l > 1) {
l -= 1;
ans = Math.min(ans, myabs(sum - 2 * get(i, j, i + l - 1, j + l - 1)));
}
}
}
System.out.println(ans);
}
private static long myabs(long x) {
return Math.abs(x);
}
private static long get(int a, int b, int c, int d) {
return g[c][d] - g[c][b-1] - g[a-1][d] + g[a-1][b-1];
}
}
1.2前缀和+哈希表
这一类题目,不少都可以使用双指针来求解,不过双指针的解法,通用性没有前缀和+哈希表强(双指针求解的话必须要满足单调性,一般来说,数组中的元素的数值不能有负数)
使用场景:一般用于求满足条件的子串/子数组个数,比如对于以i结尾的区间来说,可以使用哈希表去记录[0,i-1],[0,i-2],...,[0,0]的值,然后根据当前前缀和s[i] 和题目的要求,来去判断哈希表中是否有满足题目要求的前缀和,如果有,则增加对应计数。
LeetCode 930. 和相同的二元子数组
class Solution {
public int numSubarraysWithSum(int[] nums, int goal) {
HashMap<Integer,Integer> map=new HashMap<>();
int n=nums.length;
map.put(0, 1); // 初始化前缀和为0的情况,出现一次
int res = 0;
int[] prefixSum=new int[n+1];
//符合条件即 sum[i]-sum[j]=goal,则sum[j]=sum[i]-goal
for(int i=0,sum=0;i<n;++i){
sum+=nums[i];// 计算当前位置的前缀和
// 如果前缀和为 sum - goal 的情况已经出现过,累加到结果中
res += map.getOrDefault(sum - goal, 0);
map.put(sum, map.getOrDefault(sum, 0) + 1);
}
return res;
}
}
class Solution {
public int minSubarray(int[] nums, int p) {
long sum = 0;
for (int num : nums) {
sum += num;
}
//如果能直接整除
if (sum % p == 0) {
return 0;
}
//问题转为求一个最短的区间长度,使得区间和%p的值为sum%p ,如果不存在,返回-1
sum %= p;//得到需要被扣去的区间和大小
HashMap<Long, Integer> mp = new HashMap<>();
mp.put(0L, -1);
int n = nums.length;
int res = n;
long s = 0;
for (int i = 0; i < n; i++) {
//计算区间和%p
s = (s + nums[i]) % p;
//如果哈希表中存在val满足(s[i]-val+p)%p=sum%p,则说明存在区间满足,更新最短长度即可。
//即val%p=(s - sum + p) % p
long target = (s - sum + p) % p;
if (mp.containsKey(target)) {
res = Math.min(res, i - mp.get(target));
}
mp.put(s, i);
}
return (res == n) ? -1 : res;
}
}
2023阿里-切割环形数组
题解: 前缀和+哈希表计数+分类讨论
考虑环形切割 无非两种情况:切两边和切中间(切中间就是把中间分为一段,剩下的左右两边,因为是环形的关系,可以分成另外一段)
首先考虑无解的情况:如果数组总和为奇数,那么必定无解。
**对于切两边来说,**其实就是考虑前缀和s[i]是否等于总和的一半
对于切中间来说,枚举到第i个点时,考虑(1,i)区间有多少个满足[j,i]区间和为总和的一半,可以使用哈希表记录前缀和出现的次数,然后枚举到i时,判断是否存在有key的值为s[i]-sum的(sum为数组总和的一半),如果有,则累加对应的计数。
import java.util.*;
public class Main{
public static void main (String[] args) {
Scanner sc=new Scanner(System.in);
int n=sc.nextInt();
long[] w=new long[n+1];
long[] s = new long[n + 1];
for (int i = 1; i <= n; i++) {
w[i] = sc.nextLong();
}
//前缀和计算
for (int i = 1; i <= n; i++) {
s[i] = s[i - 1] + w[i];
}
//如果和为奇数则不可分
if (s[n] % 2 != 0) {
System.out.println("0");
}else{
long sum = s[n] / 2;
Map<Long, Long> cnts = new HashMap<>();
long res = 0;
//如果只在数组中间切一刀
for (int i = 1; i < n; i++) {
if (s[i] == sum) {
res++;
}
}
//若切两刀
for (int i = 1; i < n; i++) {
res += cnts.getOrDefault(s[i] - sum, 0L);
cnts.put(s[i], cnts.getOrDefault(s[i], 0L) + 1);
}
System.out.println(res);
}
}
}
平均数
题解:数学推导+前缀和+哈希表,下标从1开始,使用前缀和计算区间[1,i]的区间和s[i],对于以i结尾的区间,如果存在满足条件的区间[j,i],使得区间的平均数为k,我们定义区间的长度为len,则有
s
[
i
]
−
s
[
j
−
1
]
=
k
∗
l
e
n
,
其中
l
e
n
=
i
−
j
+
1
s[i]-s[j-1]=k*len,其中len=i-j+1
s[i]−s[j−1]=k∗len,其中len=i−j+1
则有
s
[
i
]
−
s
[
j
−
1
]
=
k
∗
(
i
−
j
+
1
)
s[i]-s[j-1]=k*(i-j+1)
s[i]−s[j−1]=k∗(i−j+1)
把j和i移到同一边,则有:
s
[
i
]
−
k
∗
i
=
s
[
j
−
1
]
−
(
j
−
1
)
∗
k
s[i]-k*i=s[j-1]-(j-1)*k
s[i]−k∗i=s[j−1]−(j−1)∗k
因此,当枚举到i时,只需要判断哈希表中是否存在s[i]-k*i即可,如果存在,则更新最大长度,不存在的话,就把当前的值(s[i]-k*i)和下标(i)作为哈希表的key和val存到哈希表中
举个例子,比如数组为
a
=
[
4
,
3
,
2
,
5
]
,
k
=
3
a=[4,3,2,5],k=3
a=[4,3,2,5],k=3
这里的数组下标从1开始,方便前缀和计算
一开始初始化哈希表为
m
p
[
s
[
0
]
−
0
∗
k
]
=
m
p
[
0
−
0
]
=
m
p
[
0
]
=
0
mp[s[0]-0*k]=mp[0-0]=mp[0]=0
mp[s[0]−0∗k]=mp[0−0]=mp[0]=0
-
遍历到下标
1,就是元素4的位置,计算数值s[1]-1*k=4-3=1,哈希表中不存在1,记录mp[1]=1后,跳过 -
遍历到下标2,就是元素3的位置,计算数值
s[2]-2*k=4+3-2*3=1,哈希表中存在1,更新最大长度res=max(res,i-mp[s[i]-k*i])=max(res,2-1)=1,也就是子数组【3】,找到了一个答案 -
遍历到下标3,计算数值
s[3]-3*k=4+3+2-3*3=0哈希表中存在1,更新最大长度res=max(res,i-mp[s[i]-k*i])=max(res,3-0)=3,也就是子数组【4,3,2】,找到全局最优解 -
遍历到下标4,计算数值
s[4]-4*k=4+3+2+5-4*3=2,哈希表中不存在2,记录mp[2]=4后,跳过
import java.util.HashMap;
import java.util.Map;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
long k = scanner.nextLong();
long[] w = new long[n + 1];
for (int i = 1; i <= n; i++) {
w[i] = scanner.nextLong();
}
Map<Long, Integer> mp = new HashMap<>();
mp.put(0L, 0);
long sum = 0;
int res = -1;
for (int i = 1; i <= n; i++) {
sum += w[i];
//要求s[i,j]=s[i]-s[j-1]=k*len=k*(i-j+1);
//s[i]-k*i=s[j-1]-(j-1)*k
if (mp.containsKey(sum - k * i)) {
res = Math.max(res, i - mp.get(sum - k * i));
} else {
mp.put(sum - k * i, i);
}
}
System.out.println(res);
}
}
魔法师
题解:前缀和+哈希表+位运算
对于正数来说:子区间内的负数个数为偶数即可
对于负数来说:子区间内的负数个数为奇数即可
可以使用前缀和统计[i,j]区间的负数数量 如果是奇数 则为负数 否则为偶数
注意到只需要考虑负数的奇偶性 而不需要考虑负数的具体数量 可以使用异或^(不进位的加法)来优化计算
计算的方案数为:以i结尾的子区间的方案数
对于负数方案来说 如果当前s[i]=1 需要计算前i-1个区间s[j]=0的数量,如果s[i]=0需要计算前i-1个区间 s[j]=1的数量 即求s[j]=!s[i]的数量
对于正数 直接求s[j]=s[i]的数量即可
import java.util.*;
public class Main{
public static void main (String[] args) {
Scanner sc=new Scanner(System.in);
int n=sc.nextInt();
int[] w=new int[n];
//对于正数来说:子区间内的负数个数为偶数即可
//对于负数来说:子区间内的负数个数为奇数即可
//可以使用前缀和统计[i,j]区间的负数数量 如果是奇数 则为负数 否则为偶数
for(int i=0;i<n;++i){
w[i]=sc.nextInt();
//负数记为1,正数记为0
w[i]=(w[i]>0)?0:1;
}
int[] cnts = new int[2];
cnts[0]=1;
cnts[1]=0;
//白魔法方案
long zeros = 0;
//黑魔法方案
long ones = 0;
int s = 0;
for(int i=0;i<n;++i){
s^=w[i];
zeros+=cnts[s];
ones+=cnts[1-s];
cnts[s]++;
}
System.out.println(ones + " " + zeros);
}
}
LeetCode 1371. 每个元音包含偶数次的最长子字符串
题解:前缀和+哈希表+位运算,我们只需要考虑"aeiou"这五种字符出现的次数,题目要求出现的次数是偶数的最长子串,那么对于每个字符,出现的次数只有奇数和偶数两种情况,我们可以使用二进制来表示出现的次数是奇数次还是偶数次,0代表出现次数为偶数,1代表出现次数为奇数。
可以先考虑一个简单情况,对于某一个单个字符a,出现的次数是偶数次数的最长子串,我们可以使用一个前缀和数组s去记录对应区间[0,i],字符a出现的次数为s[i],使用哈希表去记录[0,i-1]下标对应的次数和下标位置,如果在哈希表中有s[j],则最长的子串长度可以更新为res=max(res,i-mp[s[i]]),初始化mp[0]=1。
那么对于这五个字符,我们可以使用映射关系和<<运算符来去考虑,使用一个哈希表去把"aeiou"这五个字符映射到数字[0,4],那么我们就可以使用一个长度为 5 的二进制数字来表示每一个字符出现的次数是奇数还是偶数,由于出现的次数只有0和1两种情况,因此可以使用异或运算法^来表示然后采用跟上面单个字符相同的处理方式来处理。
class Solution {
public int findTheLongestSubstring(String s) {
HashMap<Character, Integer> dirc = new HashMap<Character, Integer>() {
{
put('a', 0);
put('e', 1);
put('i', 2);
put('o', 3);
put('u', 4);
}
};
HashMap<Integer, Integer> pos = new HashMap<>();
pos.put(0, -1);
int n = s.length();
int res = 0;
int state = 0;
for (int i = 0; i < n; i++) {
if (dirc.containsKey(s.charAt(i))) {
//判断当前(0,i)长度的字符串中每个元音是否都是偶数次
//如果是则state=0,反之则为1 << dirc.get(s.charAt(i))的值
state ^= (1 << dirc.get(s.charAt(i)));
}
//判断(0,i-1)的各个区间中是否存在符合要求的区间
//类似 s[j]=s[i]-sum
if (pos.containsKey(state)) {
res = Math.max(res, i - pos.get(state));
} else {
//保存(0,i)长度元音的状态和对应的索引
pos.put(state, i);
}
}
return res;
}
}
LeetCode 1915. 最美子字符串的数目
题解:位运算+状态压缩+前缀和+哈希表,与 LeetCode 1371 很像,对于题目要求统计的数目,其实可以分成两类:区间内所有字母出现的次数都是偶数次/区间内有某一个字母出现的次数为奇数次。我们使用0表示字母出现的次数为偶数,用1表示字母出现的次数是奇数。由于题目中只有'a'到'j'这十个小写英文字母,因此可以使用一个长度为 10 的二进制数来表示某一个区间字母出现次数的奇偶性,比如状态1000010000就代表字母'a'和'f'出现了奇数次,其他字母出现的次数都是偶数,可以使用前缀和+哈希表来记录区间[0,i]某一个状态出现的次数,那么枚举到当前状态state时,就可以根据上面分的两大类,来去统计对应的区间个数。
**注意:**只有0和1两个状态,可以使用异或运算符来代替+,1<<j表示枚举第j个字符出现次数的奇偶性,在这里面加法也可以使用运算符来代替,比如区间[0,i]的状态为state,区间[0,j]的状态为state1,那么对于区间[j+1,i]的状态state2一定有state1^state2=state,左右两边同时^state1,则有state2=state^state1,就可以根据这个等式,来使用哈希表求出方案数。
class Solution {
public long wonderfulSubstrings(String word) {
HashMap<Integer, Integer> mp = new HashMap<>();
mp.put(0, 1);
long res = 0;
int n = word.length();
//state 表示当前字符的奇偶状态
int state = 0;
for (int i = 0; i < n; i++) {
// 更新当前状态
state ^= (1 << (word.charAt(i) - 'a'));
// 如果当前状态已经存在,说明存在子字符串满足所有字符出现偶数次
//累加上区间中每个字母出现次数都是偶数的个数
res += mp.getOrDefault(state, 0);
// 检查所有可能的单一字符位不同的状态
for (int j = 0; j < 10; j++) {
// 计算当前状态与单一字符位不同的状态
res += mp.getOrDefault(state ^ (1 << j), 0);
}
// 更新哈希表,记录当前状态出现的次数
mp.put(state, mp.getOrDefault(state, 0) + 1);
}
return res;
}
}
3、差分
差分模板题
题目描述
输入一个长度为n的整数序列。
接下来输入m个操作,每个操作包含三个整数 l,r,c,表示将序列中[l,r]之间的每个数加上c。
请你输出进行完所有操作后的序列。
输入格式
第一行包含两个整数n和m。
第二行包含 n 个整数,表示整数序列。
接下来m 行,每行包含三个整数 l,r,c,表示一个操作.
import java.util.Scanner;
public class Main{
int[] b = new int[100010];
public void insert(int l ,int r ,int c){
b[l] += c;
b[r+1] -= c;
}
public static void main(String[] args){
new Main().test();
}
public void test(){
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
int m = scan.nextInt();
int[] a = new int[n+1];
for(int i = 1 ; i <= n ; i ++ ){
a[i] = scan.nextInt();
}
for(int i = 1;i <= n ; i ++ ){
insert(i,i,a[i]);
}
while(m-->0){
int l = scan.nextInt();
int r = scan.nextInt();
int c = scan.nextInt();
insert(l,r,c);
}
for(int i = 1;i <= n ; i ++ ){
a[i] = a[i-1] + b[i];
System.out.print(a[i] + " ");
}
}
}
class Solution {
public boolean carPooling(int[][] trips, int capacity) {
int[] diff=new int[1001];
for(int[] t:trips){
int a=t[1];
int b=t[2];
int c=t[0];
diff[a]+=c;
diff[b]-=c;
}
int sum=0;
for(int i=0;i<=1000;++i){
sum+=diff[i];
if(sum>capacity){
return false;
}
}
return true;
}
}
2023华为-塔子哥监考
题解:差分模板题,某一时刻收取的金币值,是由当前时刻监考的考场数量决定的,题目给定每个考场的开始时间a和结束时间b,相当于对区间[a,b]执行+1操作,直接使用差分数组模板即可ac。
本题有一个细节需要注意:需要找到所有操作的区间左端点最小值l_min和区间右端点最大值r_max,因为区间的值为0也是有收益的,因此要避免多计算(最后的一场监考结束,就不会赚取金币了)
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int N = 1000010;
int mod = 1000000007;
int n = scanner.nextInt();
int[] l = new int[N];
int[] r = new int[N];
int[] diff = new int[N];
int r_max = 0, l_min = 1000000000;
for (int i = 0; i < n; i++) {
l[i] = scanner.nextInt();
r[i] = scanner.nextInt();
diff[l[i]]++;
diff[r[i] + 1]--;
r_max = Math.max(r_max, r[i]);
l_min = Math.min(l_min, l[i]);
}
long res = 0;
long sum = 0;
for (int i = l_min; i <= r_max; i++) {
sum += diff[i];
if (sum == 0) {
res++;
} else if (sum == 1) {
res += 3;
} else {
res += 4;
}
}
System.out.println(res);
}
}
2023美团-天文爱好者
题解:离散化差分+哈希表计数,由于本题数据范围为
1
0
9
10^9
109,无法使用数组去模拟差分(无法申请这么多的内存,时间上来说也会超时),需要借助哈希表来实现离散化差分,对于Java,可以使用TreeMap这种数据结构来实现离散化差分
这道题可以把问题转化为统计区间中的所有点的最大权值,以及这个最大权值出现的次数,转换成这个问题之后,就使用离散化差分+哈希表计数的方式来统计,并更新最大权值和其出现的次数即可。
import java.util.*;
public class Main{
public static void main (String[] args) {
Scanner sc=new Scanner(System.in);
int n=sc.nextInt();
int[] l = new int[n];
int[] r = new int[n];
//记录出现和消失的时刻
for (int i = 0; i < n; i++) {
l[i] = sc.nextInt();
}
for (int i = 0; i < n; i++) {
r[i] = sc.nextInt();
}
TreeMap<Integer, Integer> mp = new TreeMap<>(); // 使用有序的哈希表进行离散化差分
//计算差分
for (int i = 0; i < n; i++) {
int a = l[i];
int b = r[i];
mp.put(a, mp.getOrDefault(a, 0) + 1);
mp.put(b + 1, mp.getOrDefault(b + 1, 0) - 1);
}
//统计观测到的流星各个流星数的频数
TreeMap<Integer, Integer> cnts = new TreeMap<>();
int sum = 0;
//获取出现最早的时刻
int pre = Arrays.stream(l).min().getAsInt();
for (Map.Entry<Integer, Integer> entry : mp.entrySet()) {
int u = entry.getKey();
int v = entry.getValue();
// 统计观测到流星的频数
cnts.put(sum, cnts.getOrDefault(sum, 0) + (u - pre));
//差分统计
sum += v;
pre = u;
}
int maxCnt = 0;
int maxNum = 0;
for (Map.Entry<Integer, Integer> entry : cnts.entrySet()) {
int u = entry.getKey();
int v = entry.getValue();
if (maxCnt < u) {
maxCnt = u;
maxNum = v;
}
}
System.out.println(maxCnt + " " + maxNum);
}
}




















 1113
1113

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








