小波变换教程(二十二)

小波变换网文精粹：小波变换教程(二十二)

原文：ROBI POLIKAR. THE ENGINEER'S ULTIMATE GUIDE TO WAVELET ANALYSIS：The Wavelet Tutorial

网址：http://users.rowan.edu/~polikar/WAVELETS/WTtutorial.html

二十二、离散小波变换(二)

        上述过程用数学公式可以表示如下：

                           

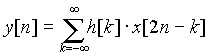
        说到这里，我们来看一下DWT到底是如何计算的：DWT通过在不同的频段利用不同的分辨率来将信号分解为粗略的近似和详细信息。DWT用到了两组函数，即尺度函数和小波函数，分别对应了低通滤波器和高通滤波器。将信号分解到不同的频段可简单地在时域将信号不断通过高通和低通滤波来实现。原始信号x[n]首先通过一个半带高通滤波器g[n]和一个半带低通滤波器h[n]。滤波之后，由于信号现在的最高频率是pi/2而不是pi，根据奈奎斯特规则，有一半的采样点可以扔掉。于是接下来进行2倍的下采样处理，即每隔一个点扔掉一个点。这就是一层的分解，并可用数学公式表示如下：

                         

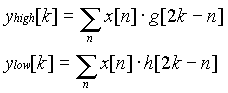
        其中yhigh[k] 和 ylow[k]分别表示经过2倍下采样处理后的高通和低通滤波器输出。上述分解过程将时间分辨率变为一半，因为仅需用一半的采样点即可表示原始信号的全部特征。但是，同时频率分辨率变为原来的两倍，因为信号的频带只有原始信号频带的一半，从而有效降低了一半的频率不确定性。上述分解过程，也即是通常所说的子带编码，还可以重复下去不断分解。在每一层的分解中，滤波和下采样会导致采样点数不断减半(因此使时间分辨率减半)和频带减半(因此使频率分辨率加倍)。整个的分解过程，即子带编码过程如图4.1所示。其中x[n]为待分解的原始信号，h[n]和g[n]分别为低通和高通滤波器。每一层的信号带宽在图中用"f"来标识。

                                

                                                                                              图 4.1. 子带编码算法 

        来看一个例子，假定原始信号x[n]的长度为512，频带范围为0到pi弧度。在第一层分解中，信号通过高通和低通滤波器，接下来再进行2倍的下采样处理。高通滤波器的输出为256个采样点（因此时间分辨率降低一半），但是频带范围为pi/2到pi(因此提高了一采样点倍的频率分辨率)。这256个采样点即为第一层DWT的系数。低通滤波器的输出也是256个采样点，其频带范围为0到pi/2。在下一层的分解中，低通滤波之后的信号再经过同样的低通和高通滤波器。经第二个低通滤波及下采样之后，信号只有128个采样点，频带范围从0到pi/4。经第二个高通滤波及下采样之后，信号也只有128个采样点，频带范围从pi/4到pi/2。第二个高通滤波器的输出信号就是第二层DWT的系数。相比第一层，此时信号的时间分辨率降低一半，频率分辨率提高一倍。相比原始信号，时间分辨率降为原来的1/4，频率分辨率提高为原来的4倍。低通滤波器的输出继续作为下一层分解的输入信号，再进行滤波及下采样的处理。这个过程一直继续下去，直到剩下2个采样点才结束分解。对于刚才的这个512点的例子，总共需要进行8层分解，每一层的输出点数均为前面一层点数的一半。最后，原始信号的DWT包括从最后一层开始的每层的高通输出。信号的DWT的数据点数与原始信号的点数是一样多的。

        原始信号中主要的频率分量，在DWT中会出现在包含这些特定频率的信号中。与傅立叶变换不同的是，这种变换保留了信号的时间信息。当然，时间的分辨率与频率所处的层数有关。如果信息的频段在高频部分，那么时间分辨率就很高，因为此时信号的采样点数还比较多。如果信息的频段在低频部分，那么时间分辨率就很低，因为此时信号只有很少的几个采样点。DWT在高频部分能获得很好的时间分辨率，在低频部分能获得很好的频率分辨率。许多实际的信号正是需要这种处理。