三角形中的正方形，三个问题

看书的时候看到一个问题：给定一个锐角三角形，画出其内接正方形

已知：给定三角形

条件：正方形且4个点pA pB pC pD都在三角形ABC上，假设点pA在边AB，pB，pC在边BC，pD在边AC

思路：假设第四个点不在边f上，会发生什么？

会发现这个正方形不固定！因为条件不够

但是把多个正方形画出来就发现，点pD的轨迹居然在一条线上！

而这条线目测是角平分线，至此，作图的问题解决，轨迹如下图

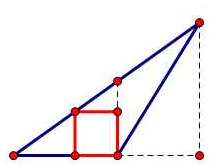
对于钝角三角形呢？很遗憾，此时的轨迹不是角平分线了，如下图。

显然：一个钝角三角形只有一个内接正方形，且正方形的两个点在最长边，很好奇这条线是什么线？？？

顺便就想到问题2了。

问题2,：该正方形边长怎么求？设边长为x ，|A pA|为y

思路：画出该内接正方形

首先pApD平行BC，相似：x/a=y/c

设bc边高为h，相似：x/h=(c-y)/c

解得x=ha/(a+h)

问题3：给定一个锐角三角形，求其内部的最大正方形的面积？（不一定内接）

思路：考虑贪心

贪心：如果最大面积正方形ABCD只有两个点在三角形边上，那么该正方形肯定能扩展其边长，直到第三个点也在三角形边上

由于此时正方形第四个顶点在角平分线上

可以看到，边长x变化的范围是0~ah/(a+h)

现在是两个顶点在边BC上，还要比较其他两条边为底的情况

初步结论：锐角三角形内最大面积是三个内接正方形面积取最大

对于钝角三角形呢，内部最大正方形面积就是内接正方形吗？

不对，比如下图，3个点的贪心不一定比4个点的贪心差

发现一个钝角三角形的内部最大面积正方形的正解：https://wenku.baidu.com/view/974272a085868762caaedd3383c4bb4cf7ecb735.html