POJ 1177 Picture (线段树)

Picture Time Limit: 2000MS   Memory Limit: 10000K Total Submissions: 9024   Accepted: 4762 Description A number of rectangular posters, photographs and other pictures of the same shape are pasted on a wall. Their sides are all vertical or horizontal. Each rectangle can be partially or totally covered by the others. The length of the boundary of the union of all rectangles is called the perimeter.  Write a program to calculate the perimeter. An example with 7 rectangles is shown in Figure 1. 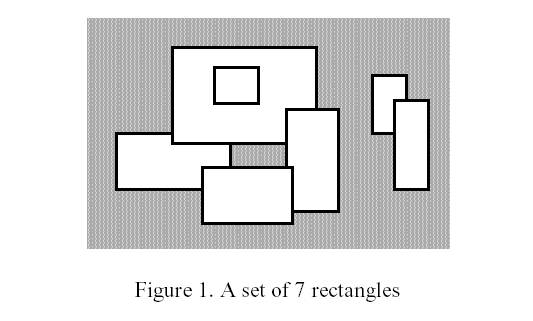 The corresponding boundary is the whole set of line segments drawn in Figure 2. 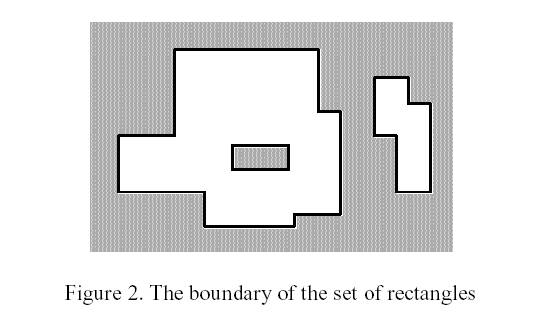 The vertices of all rectangles have integer coordinates.  Input Your program is to read from standard input. The first line contains the number of rectangles pasted on the wall. In each of the subsequent lines, one can find the integer coordinates of the lower left vertex and the upper right vertex of each rectangle. The values of those coordinates are given as ordered pairs consisting of an x-coordinate followed by a y-coordinate.  0 <= number of rectangles < 5000  All coordinates are in the range [-10000,10000] and any existing rectangle has a positive area. Output Your program is to write to standard output. The output must contain a single line with a non-negative integer which corresponds to the perimeter for the input rectangles. Sample Input 7 -15 0 5 10 -5 8 20 25 15 -4 24 14 0 -6 16 4 2 15 10 22 30 10 36 20 34 0 40 16 Sample Output 228 Source IOI 1998

 

 

题意：求矩形周长的并

思路：第一回遇见 用到扫描线的题 找了资料和看解题报告才弄懂 （PS:解题报告都不附注释的。。。）
详细讲一下扫描线的使用吧 为自己也为以后要学的人一点帮助

1.将排序后的seg数组依次输入，执query函数 flag = 1 为插入边，flag = -1 为出边 修改 count的值 同时更新len和line

2.每扫描一次，就要计算一次周长pmt，这里我们以图中的例子来讲解过程：

   首先是AB，它被插入线段树，pmt = pmt + |AB|；

   然后是EG，它被插入线段树，此时线段树的root节点的测度为|EG|的值，但由于之前之前加过|AB|，因而应该减去|AB| 即（now_l），其实就是减去|KL|，然后再加上line*2*|AK| (水平的长度)，这里的line的值是未插入EG时线段树的根节点的line值。

 

 

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>

using namespace std;

#define L(rt) (rt<<1)
#define R(rt) (rt<<1|1)

const int N=5010;

struct node{
    int l,r;
    int lb,rb;   //左右端点是否被覆盖
    int count,line,len; //count 被覆盖的次数  line 所包含区间的数量 len 是区间长度（测度）
}tree[N*3];

struct data{
    int x,y1,y2;
    int flag;   //flag 1表示为入边，-1表示为出边
}seg[N<<1];

int y[N<<1];    //记录y坐标

int cmp(data a,data b){ //x升序 x相同时 入边在前
    if(a.x!=b.x)
        return a.x<b.x;
    return a.flag>b.flag;
}

void build(int l,int r,int rt){
    tree[rt].l=l;
    tree[rt].r=r;
    tree[rt].len=tree[rt].line=tree[rt].count=0;
    if(l+1==r)
        return ;
    int mid=(l+r)>>1;
    build(l,mid,L(rt));
    build(mid,r,R(rt));
}

void update(int rt){    //更新测度 和 line的值,获得以当前接点为根的树被覆盖的区间总长度 被覆盖区间的总数
    if(tree[rt].count>0){
        tree[rt].len=y[tree[rt].r]-y[tree[rt].l];
        tree[rt].line=tree[rt].lb=tree[rt].rb=1;
    }else if(tree[rt].l+1==tree[rt].r){
        tree[rt].len=0;
        tree[rt].line=tree[rt].lb=tree[rt].rb=0;
    }else{  //由左右结点的值 确定父亲结点的值
        tree[rt].len=tree[L(rt)].len+tree[R(rt)].len;
        tree[rt].lb=tree[L(rt)].lb;
        tree[rt].rb=tree[R(rt)].rb;
        tree[rt].line=tree[L(rt)].line+tree[R(rt)].line-tree[L(rt)].rb*tree[R(rt)].lb;
    }
}

void query(int flag,int l,int r,int rt){
    if(y[tree[rt].l]==l && y[tree[rt].r]==r){
        tree[rt].count+=flag;
        update(rt);
        return ;
    }
    int mid=y[(tree[rt].l+tree[rt].r)>>1];
    if(r<=mid)
        query(flag,l,r,L(rt));
    else if(l>=mid)
        query(flag,l,r,R(rt));
    else{
        query(flag,l,mid,L(rt));
        query(flag,mid,r,R(rt));
    }
    update(rt);
}

int main(){

    //freopen("input.txt","r",stdin);

    int n,cnt;
    int x1,y1,x2,y2;
    while(~scanf("%d",&n)){
        cnt=0;
        for(int i=0;i<n;i++){
            scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
            seg[cnt].x=x1, seg[cnt].y1=y1, seg[cnt].y2=y2;
            seg[cnt].flag=1, y[cnt++]=y1;
            seg[cnt].x=x2, seg[cnt].y1=y1, seg[cnt].y2=y2;
            seg[cnt].flag=-1, y[cnt++]=y2;
        }
        sort(seg,seg+cnt,cmp);
        sort(y,y+cnt);
        int len=unique(y,y+cnt)-y-1;    //离散化
        build(0,len,1);
        int pmt=0,now_m=0,now_l=0;  //pmt 周长
        for(int i=0;i<cnt;i++){
            query(seg[i].flag,seg[i].y1,seg[i].y2,1);
            if(i>0)
                pmt+=2*now_l*(seg[i].x-seg[i-1].x); //水平x的长度
            pmt+=abs(tree[1].len-now_m);     //y的长度
            now_m=tree[1].len;  
            now_l=tree[1].line;
        }
        printf("%d\n",pmt);
    }
    return 0;
}

 

转载于:https://www.cnblogs.com/jackge/archive/2013/04/24/3039451.html