多项式分布是二项分布的推广。二项分布(也叫伯努利分布)的典型例子是扔硬币,硬币正面朝上概率为p, 重复扔n次硬币,k次为正面的概率即为一个二项分布概率。而多项分布就像扔骰子,有6个面对应6个不同的点数。二项分布时事件X只有2种取值,而多项分布的X有多种取值,多项分布的概率公式为
这个公式看上去像是莫名其妙地冒出来的,想要了解它首先必须要知道组合数学中的多项式定理。
多项式定理:当n是一个正整数时,我们有
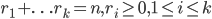 。
。
这个多项式定理的推导如下,将式子左边展开
上面的式子是由n个因子相乘得到,而它的展开式可以看做在每个式子里选取某一个xi,总共选取n个xi相乘,所以所有的展开式项都会有
这样的公有项,而且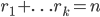
这样的话,我们可以把问题看成在n个式子里,先选取r1个x1,然后选取r2个x2,最后选取rk个xk,然后求有多少种方法。类似把n 个球放到k个不同的盒子里的方法有多少种,我们得到
所以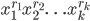
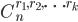
再来看之前的多项分布的概率公式,假设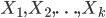
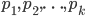
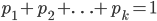
我们将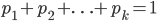
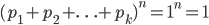
转自:http://www.crescentmoon.info/?p=9#more-9










 本文探讨了二项分布及其推广形式——多项式分布。介绍了这两种概率分布的基本概念及应用,并通过组合数学中的多项式定理来推导多项式分布的概率公式。
本文探讨了二项分布及其推广形式——多项式分布。介绍了这两种概率分布的基本概念及应用,并通过组合数学中的多项式定理来推导多项式分布的概率公式。
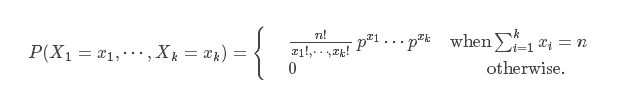
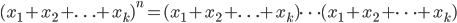
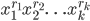
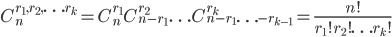
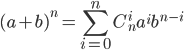
















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








