[HOT 100] 0687. 最长同值路径-CSDN博客

本文链接：https://blog.csdn.net/apple_74262176/article/details/147662715

文章目录

1. 题目链接

687. 最长同值路径 - 力扣（LeetCode）

2. 题目描述

给定一个二叉树的 root ，返回最长的路径的长度，这个路径中的每个节点具有相同值。这条路径可以经过也可以不经过根节点。

两个节点之间的路径长度由它们之间的边数表示。

3. 题目示例

示例 1 :

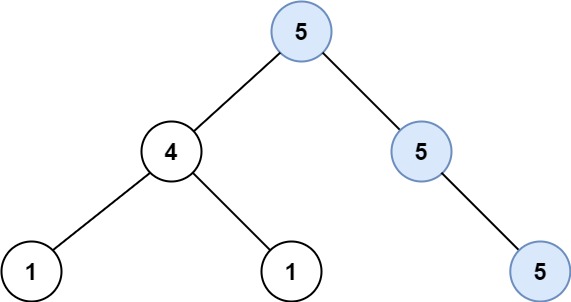
输入：root = [5,4,5,1,1,5]
输出：2

示例 2 :

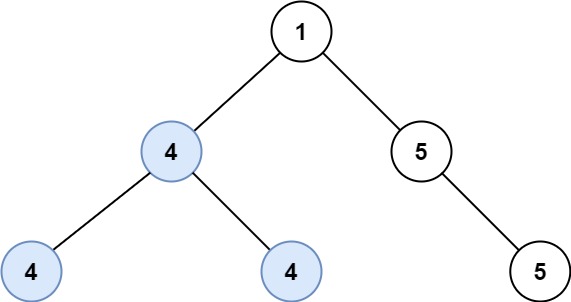
输入：root = [1,4,5,4,4,5]
输出：2

4. 解题思路

问题理解：
- 需要找到二叉树中最长的路径，路径上所有节点值相同
- 路径长度按边数计算（节点数-1）
- 路径可以不经过根节点
关键思路：
- 后序遍历计算每个节点的同值链长度
- 对于每个节点，计算其作为路径转折点时的路径长度
- 维护全局最大值
递归设计：
- 基本情况：空节点返回-1（使得叶子节点计算后为0）
- 递归计算左右子树的同值链长度
- 如果子节点值不同，则重置对应链长为0
- 更新全局最大值（左右链拼接）
- 返回当前节点的最大同值链长度
链长与路径长：
- 链长：从当前节点向下延伸的同值路径边数
- 路径长：可能由两条链拼接而成

5. 题解代码

class Solution {
    private int ans; // 存储最终结果（最长同值路径长度）

    public int longestUnivaluePath(TreeNode root) {
        dfs(root); // 从根节点开始深度优先搜索
        return ans; // 返回最长同值路径长度
    }

    private int dfs(TreeNode node) {
        if (node == null) {
            return -1; // 空节点返回-1，这样叶子节点计算时+1后为0
        }
        
        // 递归计算左子树的最大同值链长度（+1表示包含当前边）
        int lLen = dfs(node.left) + 1;
        // 递归计算右子树的最大同值链长度（+1表示包含当前边）
        int rLen = dfs(node.right) + 1;
        
        // 如果左子节点存在且值不同，重置左链长度为0
        if (node.left != null && node.left.val != node.val) lLen = 0;
        // 如果右子节点存在且值不同，重置右链长度为0
        if (node.right != null && node.right.val != node.val) rLen = 0;
        
        // 更新全局最大值（左右链拼接的总长度）
        ans = Math.max(ans, lLen + rLen);
        
        // 返回当前子树的最大同值链长度（只能选择左右链中的一条）
        return Math.max(lLen, rLen);
    }
}