A星寻路算法

1、寻路规则
A*寻路其实就是对广度寻路的优化（广度寻路太傻所有可能的路都走），最大不同就是增加了对角线的四个方向并且增加了相应的权重去判断选取最小的权重所对应的路径去走，那么最终总的权重就是最小，此时就是最短路径。
需要说明的是，权重的计算：
F=G+H，其中F为某点到终点的权重，G为起始点到当前点的权重，H为当前点到终点的预估权重。
H的计算公式为：（（终点位置行-起点位置行）+（终点位置列-起点位置列））*预估权值（注：H不考虑障碍物啥的，只考虑直线距离）
G就是每走一个方向，如上下左右就加10，如对角线的话就是加14（注：程序中是这样定义并且实现的）。
2、程序实现
在程序实现中基本与广度寻路大差不差，就是增加了寻找最小F与四个对角线方向而已还有就是计算H的权重的函数。
3、具体程序如下：

// A星寻路算法.cpp : 定义控制台应用程序的入口点。
//

#include "stdafx.h"
#include<vector>
#include<iostream>
using namespace std;

#define ROW 11
#define COL 11

#define ZXDJ 10 //直线代价
#define XXDJ 14 //斜线代价
#define YGDJ 10 //预估代价

enum emNodeDir
{
	em_Up,
	em_Down,
	em_Left,
	em_Right,
	em_LUP,//左上
	em_LDown,//左下
	em_RUP,//右上
	em_RDown,//右下
};

int gMap[ROW][COL] = {         //9
		{ 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1 },
		{ 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1 },
		{ 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1 },
		{ 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1 },
		{ 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1 },
		{ 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1 },
		{ 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1 },
		{ 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1 },
		{ 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1 }, //8
		{ 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1 },
		{ 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1 }
};


struct MapNode
{
	int value;//值
	bool isWalk;//是否走过
};

struct MapPoint
{
	int row;
	int col; 
	int f, g, h;//f是衡量某个点到终点的代价
	//g是起始点到当前点以及付出的代价 h 为已经付出的代价，不考虑障碍物只考虑直线距离
};

struct treeNode
{
	MapPoint pos;//当前点的位置
	treeNode* parent;//父节点
	vector<treeNode*>Child;//子节点
};

MapNode gMapNode[ROW][COL];

void InitMapNode();//初始化地图点
treeNode* CreatNode(MapPoint point);//增加新的节点
bool isCanWalk(MapPoint point);//判断是否可以走
int GetHValue(MapPoint startPos, MapPoint endPos);//计算H值


int _tmain(int argc, _TCHAR* argv[])
{
	MapPoint startPos = { 4, 1 }, endPos = { 8, 9 };
	gMapNode[startPos.row][startPos.col].isWalk = true;

	InitMapNode();
	treeNode* pRoot = CreatNode(startPos);
	treeNode* currentPos = pRoot;

	vector<treeNode*>nextNodeVec;
	vector<treeNode*>::iterator minNodeiter;//最小节点迭代器

	bool isWalkEnd = false;

	while (!isWalkEnd)
	{
		for (int i = 0; i < 8; i++)
		{
			treeNode* pNew = new treeNode;
			memset(pNew, 0x00, sizeof(treeNode));
			pNew->pos = currentPos->pos;

			switch (i)
			{
			case em_Up:
				pNew->pos.row--;
				pNew->pos.g += ZXDJ;
				break;//跳出switch选择结构
			case em_Down:
				pNew->pos.row++;
				pNew->pos.g += ZXDJ;
				break;
			case em_Left:
				pNew->pos.col--;
				pNew->pos.g += ZXDJ;
				break;
			case em_Right:
				pNew->pos.col++;
				pNew->pos.g += ZXDJ;
				break;
			case em_LDown://左下
				pNew->pos.g += XXDJ;
				pNew->pos.row++;
				pNew->pos.col--;
				break;
			case em_RDown://右下
				 pNew->pos.row++;
				 pNew->pos.col++;
				pNew->pos.g += XXDJ;
				break;
			case em_LUP://左上
				pNew->pos.g += XXDJ;
				pNew->pos.row--;
				pNew->pos.col--; 
				break;
			case em_RUP://右上
				pNew->pos.g += XXDJ;
				pNew->pos.row--;
				pNew->pos.col++; 
				break;
			}
			if (isCanWalk(pNew->pos))
			{
				pNew->pos.h = GetHValue(pNew->pos, endPos);//H值
				pNew->pos.f = pNew->pos.g + pNew->pos.h;//F值

				currentPos->Child.push_back(pNew);//将该点入树

				pNew->parent = currentPos;//上一个节点作为当前节点的父亲

				nextNodeVec.push_back(pNew);//将新节点放入数组，需要找到最小的f值
			}
			else
			{
				delete pNew;
			}
		}
		//找数组中f值最小的
		vector<treeNode*>::iterator it = nextNodeVec.begin();
		minNodeiter = it;
		for ( ; it!= nextNodeVec.end();it++)//遍历这一层或者说当前节点可能要走的所有点
		{
			if ((*minNodeiter)->pos.f > (*it)->pos.f)//找出最小的f值
			{
				minNodeiter = it;
			}
		}
		currentPos = *minNodeiter;//最小的点作为当前点
		
		gMapNode[currentPos->pos.row][currentPos->pos.col].isWalk = true;//标记已经走过

		nextNodeVec.erase(minNodeiter);//这个点已经走过，从数组中移除
		if (currentPos->pos.col == endPos.col&&currentPos->pos.row == endPos.row)
		{
			isWalkEnd = true;
			break;
		}

		if (nextNodeVec.size()==0)
		{
			break;
		}
	}
	if (isWalkEnd==true)
	{
		printf("找到了终点了");
		cout << endl;
		printf("Path:");
		while (currentPos)
		{
			printf("(%d,%d)", currentPos->pos.row, currentPos->pos.col);
			currentPos = currentPos->parent;
		}

		printf("\n");
	}
	else
	{
		printf("找不到出口");
	}

	return 0;
}

void InitMapNode()
{
	for (int i = 0; i < ROW; i++)
	{
		for (int j = 0; j < COL; j++)
		{
			gMapNode[i][j].value = gMap[i][j];
		}
	}
}

treeNode* CreatNode(MapPoint point)
{
	treeNode* pNode = new treeNode;
	pNode->pos = point;
	pNode->parent = 0;
	return pNode;
}

bool isCanWalk(MapPoint point)
{
	if (point.row>=ROW || point.row<0 || point.col>=COL||point.col<0)
	{
		return false;
	}

	if (gMapNode[point.row][point.col].value==1||gMapNode[point.row][point.col].isWalk==true)
	{
		return false;
	}

	return true;
}

int GetHValue(MapPoint startPos, MapPoint endPos)
{
	int x = abs(endPos.col - startPos.col);
	int y = abs(endPos.row - startPos.row);

	return (x + y)*YGDJ;
}

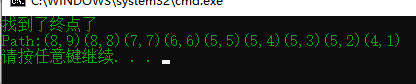
4、结果展示