堆与堆排序

参考

1 http://www.cnblogs.com/Anker/archive/2013/01/23/2873422.html

2 http://blog.csdn.net/morewindows/article/details/6709644/

3 http://blog.csdn.net/hguisu/article/details/7776068

堆排序的时间复杂度O(N*logN)的排序算法，先看下二叉堆的定义。

实际上就是一颗完全二叉树（Complete Binary Tree）：在最后一层，并不是所有的节点都拥有子节点（其他层的节点拥有子节点--而且使用拥有两个子节点）。

二叉堆有两个特点

1 父节点的值大于等于（小于等于）字节点的值

2 每个节点的左子树和右每一个子节点都是一个（最大二叉堆或最小二叉堆）

当父节点的值总是大于等于子节点的值时，称作最大堆。当父节点的值总是小于等于子节点的值的时候，叫做最小堆。

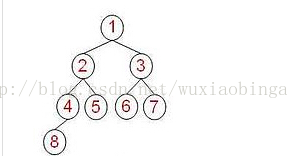
           10个用数组表示节点描述建堆、堆排序过程。

建堆过程

       max-heappify 保持堆

       build-heap 构建堆

       heap-sort 堆排序

1 保持堆的算法源码

	/**
	 * 大顶堆,数组下标从0开始 
	 * @param a       数组
	 * @param length  待排序的元素个数
	 * @param i       当前节点--目标是要把这个节点调整成堆
	 */
	public static void adjustDown(int a[], int length, int i) {
		// 左右孩子
		for (;;) {
			int maxIndex = i;

			int leftIndex = i * 2 + 1;
			int rightIndex = i * 2 + 2;
			// 选择 a[i] 和 左右子节点的中最大的值
			if (leftIndex < length - 1 && a[leftIndex] > a[i]) {
				maxIndex = leftIndex;
			}

			if (rightIndex < length && a[rightIndex] > a[maxIndex]) {
				maxIndex = rightIndex;
			}

			// 当前节点 它的左孩子 右孩子，满足 最大堆
			if (maxIndex == i) {
				break;
			} else {
				// 交换 当前节点和孩子节点中最大的
				int temp = a[i];
				a[i] = a[maxIndex];
				a[maxIndex] = temp;
				i = maxIndex;
				continue;
			}
		}
	}

2 构建堆源码：

	/**
	 * 从下向上，从右到左第一个非叶子结点； 如果数组下标从0开始，start = (a.length - 2 ) / 2
	 * 
	 * @param a
	 */
	public static void buildHeap(int[] a) {
		for (int i = (a.length - 2) / 2; i >= 0; i--) {
			adjustDown(a, a.length, i);
		}
	}

3 堆排序源码：

	/**
	 * a[0] 是最大的元素，和最后一个元素交换位置，即a[length - 1]，然后调整a[0] 成为最大堆
	 * 迭代N次，每一次调整时间复杂度最大OlogN，总的时间复杂度 O(NlogN)
	 * @param a 输入参数一个大顶堆
	 */
	public static void heapSort(int[] a) {
		for (int i = a.length; i > 0; i--) {
			int temp = a[0];
			a[0] = a[i - 1];
			a[i - 1] = temp;
			adjustDown(a, i - 1, 0);
		}
	}

       第一步 index=4 先找到最后一个有子结点的结点[max-1] / 2，先让他的两个子结点进行比较，找到大的值再和父结点的值进行比较。如果父结点的值小，则子结点和父结点进行交换，交换之后再往下比较。然后一步步递归上去，直到所在结点的位置是0号位置跳出。

       最后一个有子节点的节点的index等于4。先比较两个孩子节点中比较大的值，和a父节点比较。a[i]比较 a[4] < a[4*2 + 1]、a[4*2 + 2]，交换父节点和子节点。

      第二步 index = 3，先比较左孩子，a[3] < a[3 * 2 + 1 ]，12 < 32 , 交换。

       第三步 index = 2

堆排序是否是稳定的排序，为什么？