【问题描述】
小沐同学确信所有问题都有个多项式时间算法,为了证明,他决定自己去当一次旅行商,在上路之前,小 X 需要挑选一些在路上使用的物品,但他只有一个 能装体积为 m 的背包。显然,背包问题对小沐来说过于简单了,所以他希望你来帮他解决这个问题。
小沐可以选择的物品有 n样,一共分为甲乙丙三类:
1.甲类物品的价值随着你分配给他的背包体积变化,它的价值与分配给它的体积满足函数关系式,v(x) = A*x^2-B*x,x表示分配给该物品的体积,为非负整数,A,B是每个甲类物品的两个参数。注意每个体积的甲类物品只有一个。
2.乙类物品的价值 A和体积 B都是固定的,但是每个乙类物品都有个参数C,表示这个物品可供选择的个数。
3.丙类物品的价值 A和体积 B也是固定的,但是每个丙类物品可供选择的个数都是无限多个。
你最终的任务是确定小沐的背包最多能装有多大的价值上路。
【输入格式】
第一行两个整数 n,m,表示背包物品的个数和背包的体积;
接下来 n行,每行描述一个物品的信息。第一个整数 x,表示物品的种类:
若 x 为1表示甲类物品,接下来两个整数 A,B,为A类物品的两个参数;
若 x 为2表示乙类物品,接下来三个整数 A,B,C。A表示物品的价值,B表示它的体积,C 表示它的个数;
若 x 为3表示丙类物品,接下来两个整数A,B。A表示它的价值,B表示它的体积。
【输出格式】
仅一行为一个整数,表示小 X的背包能装的最大价值。
【输入样例】
【样例1】
1 0
1 1 1
【样例2】
4 10
2 1 2 1
1 1 2
3 5 2
2 200 2 3
【输出样例】
【样例1】
0
【样例2】
610
【数据范围】
对于50%的数据,只有乙和丙两类物品;
对于70%的数据,1<=n<=100, 1<=m<=500,0<=A,B,C<=200;
对于100%的数据,1<=n<=100, 1<=m<=2000,0<=A,B,C<=200;
【来源】
复赛模拟题
Code[VS]5226 原题传送矩阵
重庆一中题库 原题传送矩阵
【思路梳理】
背包问题,互相伤害,乙丙显然是一样的思路很容易解决主要还是看甲类:枚举给甲类的第i样物品分配多少即可!!!
可以证明的是:如果要选择某样甲类物品i,只要它的参数a[i].A是一个正数,那么显然选择其的体积越大,就越划算,换句话来说:这个物品一定。不严格证明如下:
当a[i].A是一个正数时,其价值与体积成二次函数关系:
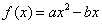
定义域为该物品能够选取的体积,值域为其对应的价格根据初等数学知识可以知道,二次函数为凹函数,那么其选取的体积越大,价值也就越大是必然的,显然我们还可以根据图像知道斜率也随之增大,也就是说单位体积的价值在增大,那么选取x个单位体积的该物品一定比选取x-1个单位的该物品的结果更优。
可列出如下的状态函数&状态转移方程,时间复杂度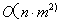
d(i,j)=从前i样物品中任意选择总体积不超过j的物品所能够形成的最大价值
d[i][j]=
Case1: max{ d(i-1,j-x)+a[i].A*x*x-a[i].B*x | 0<=x<=j,x代表选择分配的体积 }
Case2:max{d(i-1,j-k*a[i].B)+a[i].A*k | 0<=k<=min(a[i].C,j/a[i].B)}
Case 3: max( d(i-1,j-k*a[i].B)+a[i].A*k | 0<=k<=j/a[i].B )
【Cpp代码】
#include<cstdio>
#include<cstring>
#include<iostream>
#define maxn 105
#define maxm 2005
using namespace std;
int n,m,d[maxm];
struct data
{
int type,A,B,C;
}a[maxn];
void dp()
{
//d(i,j)=从前i样物品中任意选择总体积不超过j的物品所能够形成的最大价值
// Case 1: max{ d(i-1,j-x)+a[i].A*x*x-a[i].B*x | 0<=x<=j,x代表选择分配的体积 }
//d(i,j)= { Case 2: max{ d(i-1,j-k*a[i].B)+a[i].A*k | 0<=k<=min(a[i].C,j/a[i].B) }
// Case 3: max( d(i-1,j-k*a[i].B)+a[i].A*k | 0<=k<=j/a[i].B
for(int i=1;i<=n;i++)
{
if(a[i].type==1)
{
for(int j=m;j>=0;j--)
for(int x=j;x>=0;x--)
d[j]=max(d[j],d[j-x]+a[i].A*x*x-a[i].B*x);
}
if(a[i].type==2)
{
for(int j=m;j>=0;j--)
for(int k=a[i].C;k>=0;k--)if(j-k*a[i].B>=0)
d[j]=max(d[j],d[j-k*a[i].B]+a[i].A*k);
}
if(a[i].type==3)
{
for(int j=a[i].B;j<=m;j++)
d[j]=max(d[j],d[j-a[i].B]+a[i].A);
}
}
cout<<d[m];
}
int main()
{
// freopen("in.txt","r",stdin);
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i].type);
if(a[i].type==1) scanf("%d%d",&a[i].A,&a[i].B);
else if(a[i].type==2)
scanf("%d%d%d",&a[i].A,&a[i].B,&a[i].C);
else if(a[i].type==3)
{
scanf("%d%d",&a[i].A,&a[i].B);
a[i].C=2005;//物品的体积至少为1,背包最大容积为2000,所以可以认为2005为无限个
}
}
dp();
return 0;
}
























 762
762

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








