ps:概率论说实话,它不会有什么小巧思、小技巧这些,大家只要把题目看懂,知道用什么公式(当然前提是把公式记住,公式记住了就包过了,然后都不需要特别理解,只要知道在哪用,就能考个较高分了),所以本篇就是提炼公式,方便大家一起记忆,然后让大家知道能在哪里用。
概率论的基本概念
概率模型
| 概型类型 | 核心特征 | 概率计算公式 | 典型例子 |
|---|---|---|---|
| 古典概型 |
1. 基本事件有限个 2. 每个基本事件等可能 |
a = 事件A包含的基本事数; b = 试验的基本事件总数 | 掷骰子求点数为偶数的概率 |
| 几何概型 |
1. 基本事件无限个 2. 基本事件均匀分布于几何区域 |
| 区间[0,5]随机取数落在[1,3]的概率 |
| 伯努利概型 |
1. n次独立重复试验 2. 每次试验仅两种结果(成功 / 失败) 3. 单次成功概率p固定 |
k为成功的次数; q = 1 - p | 抛硬币 5 次恰好 3 次正面的概率 |
概率关系
| 特征维度 | 互斥关系 | 独立关系 |
|---|---|---|
| 本质 | 事件不能同时发生(集合无交集) | 事件发生互不影响(概率满足乘积公式) |
| 概率判定条件 |
(注意:互斥能推出P(AB)=0,但P(AB)=0不一定互斥) |
(充要条件) |
| 适用场景 | 单次试验的不同结果(如一次掷骰子的不同点数) | 多次独立试验的结果(如两次抛硬币) |
| 特殊情况 | 若 P(A)>0 且 P(B)>0,则互不相容一定不独立 | 若 P(A)=0 或 P(B)=0,则事件既独立又可能互不相容 |
概率公式
加法公式
- 通用形式:
- 互斥特例:
条件概率公式
设P(B) > 0,在事件B发生的条件下,事件A发生的概率为:
乘法公式
- 通用形式:
- 独立特例:
全概率公式
前提:事件组A1,A2,...,An两两互斥;(完备事件组);P(Ai) > 0(i = 1, 2, ..., n)。
贝叶斯公式
前提:同全概率公式的完备事件组A1,A2,...,An,且P(B) > 0。
随机变量
分布函数
设X是一个随机变量,分布函数F(x)定义为:
其含义是:随机变量X取值小于等于x的概率。
单调性:若x1 < x2,则F(x1) ≤ F(x2)。
有界性:0 ≤ F(x) ≤ 1。
概率计算:对任意实数a,b(a < b),有 。
离散型随机变量
取值为有限个或可列无限个的随机变量
分布律(概率质量函数):设 X 的可能取值为 x1, x2, ..., xn, ...,则 P{X = xk} = pk, k = 1, 2, ...称为 X 的分布律,常用表格形式表示:
| X | x1 | x2 | ··· | xn | ··· |
|---|---|---|---|---|---|
| P | p1 | p2 | ··· | pn | ··· |
三个重要离散型分布
| 分布类型 | 符号 | 分布律 | 适用场景 | 核心参数 |
|---|---|---|---|---|
| 0-1 分布 |
| 单次伯努利试验(只有两种结果) | ||
| 二项分布 |
| n 重伯努利试验中成功的次数 | ||
| 泊松分布 |
| 稀有事件发生的次数(如事故、故障数) |
补充关系:当n很大、p很小时,二项分布可近似为泊松分布,即 。
连续型随机变量
取值充满某个区间,且存在非负可积函数f(x),使得其分布函数可表示为积分形式的随机变量。
概率密度函数:满足 的函数 f(x) 称为X的概率密度函数。
概率密度的性质:
- 非负性:
;
- 归一性:
;
- 概率计算:对于任意 a ≤ b,有
。
分布函数:是连续函数,且在f(x)的连续点处有
三个重要连续型分布
| 分布类型 | 符号 | 概率密度 f(x) | 适用场景 | 核心参数 |
|---|---|---|---|---|
| 均匀分布 |
| 试验结果在区间 (a,b) 内均匀出现 | ||
| 指数分布 |
| 描述寿命、等待时间等 | ||
| 正态分布 | 自然界大量随机现象(如身高、成绩) |
标准正态分布:
- 当
时,记为
,其密度函数为
,分布函数为
;
- 一般正态分布可以通过标准化
计算概率。
随机变量函数的分布
设 X 是随机变量,y = g(x)是连续函数,则 Y = g(X) 也是随机变量,需根据 X 的类型求 Y 的分布。
1.离散型随机变量函数的分布
设 X 的分布律为 ,则 Y = g(X) 的分布律求解步骤:
- 计算 Y 的可能取值:
;
- 合并相同的
对应的概率:
2.连续型随机变量函数的分布
设 X 的概率密度为 ,求 Y = g(x) (函数 g(x) 为单调函数)的概率密度
,常用分布函数法:
,其它
其中: 分别为 g(x) 的最大值,最小值;h(y) 是 g(x) 的反函数。
多维随机变量
二维随机变量的边缘分布
1.二维离散型随机变量:联合分布律与边缘分布律
1)联合分布律
设二维离散型随机变量(X, Y)的可能取值为 (xi, yi) (i,j = 1, 2, ...),则称
为(X, Y) 的联合分布律
2)边缘分布律
关于 X 的边缘分布律:固定 X = xi,对所有 j 的概率求和,即
关于 Y 的边缘分布律:固定 X = yi,对所有 i 的概率求和,即
2.二维连续型随机变量;联合概率密度与边缘概率密度
1)联合概率密度
设二维连续型随机变量 (X,Y) 的分布函数为 F(x,y) = P{ X ≤ x,Y ≤ y },若存在非负可积函数 f(x,y),使得对任意实数 x,y 有:
则称 f(x, y) 为 (X, Y) 的联合概率密度。
2)边缘概率密度
关于 X 的边缘概率密度:对联合概率密度 f(x, y) 关于 y 积分,即
关于 Y 的边缘概率密度:对联合概率密度 f(x, y) 关于 x 积分,即
性质:
随机变量独立性的判别
定义:联合分布律等于两个边缘分布律的乘积
则称随机变量 X 与 Y 相互独立。
1.离散型随机变量的独立性判别
对所有 i, j,有
2.连续型随机变量的独立性判断
对几乎所有的 x, y,有
二维离散型随机变量函数的分布律
设二维随机变量 (X, Y) 的联合分布律为 P{ X = xi, Y = yi } = pij, Z = g(X, Y) 是 X, Y 的函数,则 Z 为离散型随机变量,其分布律:
1.确定 Z 的所有可能取值
计算 ,整理得到 Z 的不同取值
2.计算每个 zk 对应的概率
对所有满足 g(xi, yi) = zk 的 (i, j) 对应的概率求和,
二维连续型随机变量函数的分布(和、最大值、最小值)
设二维连续型随机变量 (X, Y) 的联合概率密度为 f(x, y),Z = g(X, Y),采用分布函数法:
先求 Z 的分布函数 ,再求导得概率密度。
1.和的分布:Z = X + Y
1)分布函数
2)概率密度
对 Fz(z)求导,得
若 X 与 Y 相互独立,则(卷积公式)
特例:若 ,且 X 与 Y 独立,则
例题:

2.最大值的分布:Z = max( X, Y )
假设 X 与 Y 相互独立,边缘分布函数分别为 Fx(x) 和 Fy(y)。
1)分布函数
2)概率密度
3.最小值的分布:Z = min( X, Y )
假设 X 与 Y 相互独立,边缘分布函数分别为 Fx(x) 和 Fy(y)。
1)分布函数
2)概率密度
随机变量的数字特征
随机变量的期望
1)离散型随机变量
设离散型随机变量 X 的分布律为 P{ X = xk } = pk, k = 1, 2, ...,则 X 的数学期望(简称期望或均值) :
2)连续型随机变量
设连续型随机变量 X 的概率密度为 f(x),则 X 的期望:
如果求的是 E(g(X)) ,概率密度是不变的:
期望的核心性质:
- 常数的期望:
(C为常数)
- 数乘性质:
(C为常数)
- 加法性质:
- 独立乘积性质:若 X 与 Y 独立,
随机变量的方差
方差的核心性质:
- 常数的方差:
(C为常数)
- 数乘性质:
(C为常数)
- 独立加法性质:若 X 与 Y 相互独立,则
- 方差非负性:
,且
的充要条件是
六大重要分布的期望与方差
| 分布类型 | 符号 | 期望 E(X) | 方差 D(X) |
|---|---|---|---|
| 0-1 分布 | |||
| 二项分布 | |||
| 泊松分布 | |||
| 均匀分布 | |||
| 指数分布 | |||
| 正态分布 |
协方差与相关系数
1)协方差
计算公式:
核心性质:
-
-
(C为常数)
-
(a,b为常数)
-
- 方差与协方差的关系:
2)相关系数
计算公式:
核心性质:
- 有界性:
- 不相关性:若
,则称 X 与 Y 不相关(充要条件);若 X 与 Y 相互独立,则 X 与 Y 一定不相关,但反之不成立。
大数定理与中心极限定理
切比雪夫不等式的应用
设随机变量 X 的期望 ,方差
存在,则对任意
,有:
等价形式:
核心特点:
- 不需要知道 X 的具体分布,只要期望和方差存在即可使用。
- 得到的概率界不是精确值,而是一个范围,一般不会直接拿这个来估计概率的,而是用中心极限定理。
例题:
大数定理的应用(一般都不会用来做题,了解一下就行)
1)切比雪夫大数定理(独立但不一定同分布)
2)辛钦大数定理(独立同分布,仅需期望存在)
3)伯努利大数定理(频率趋近于概率)
中心极限定理的应用(常用)
核心特点:大量独立同分布的随机变量之和,无论原分布是什么,其极限分布都是正态分布。
1)林德伯格-列维定理(独立同分布)
设随机变量 X 的期望 ,方差
,
是标准正态分布 N(0, 1) 的分布函数。
当 n 充分大时,,也就是
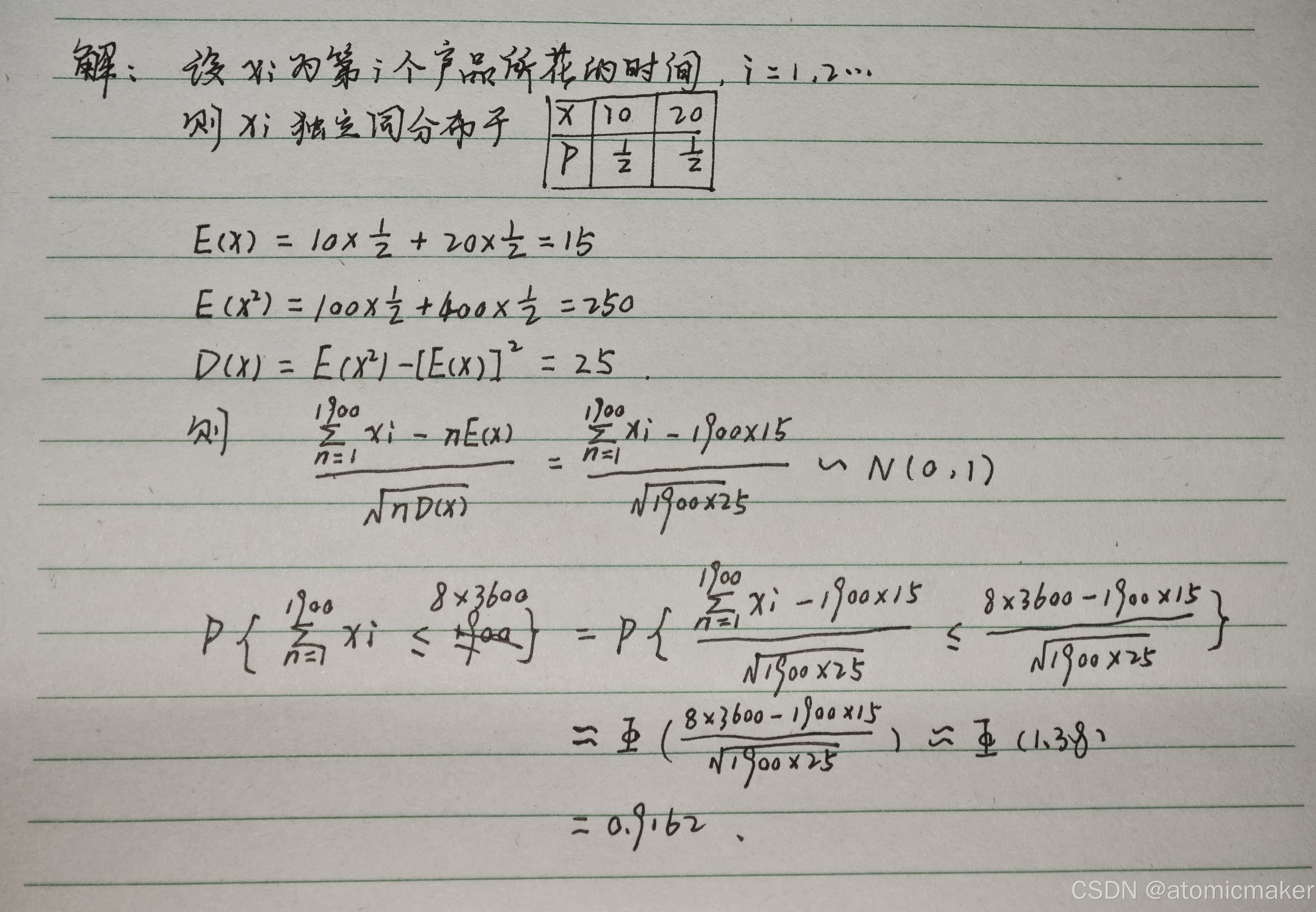
2)棣莫弗-拉普拉斯定理(二项分布的正态近似)
设 X ~ B(n, p)(n重伯努利试验成功次数),则对任意实数 x:
当 n 充分大时,也就是
例题:





















 1107
1107

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








