问题模型:
给定一个加权的有向图,满足:
(1)容量限制条件:
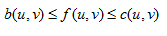
(2)流量平衡条件:
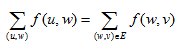
(2)中的 即除了源汇外,所有点都满足流量平衡条件,则称G为有源汇网络;否则
即除了源汇外,所有点都满足流量平衡条件,则称G为有源汇网络;否则 ,即不存在源汇,所有点都满足流量平衡条件,则称G为无源汇网络。
,即不存在源汇,所有点都满足流量平衡条件,则称G为无源汇网络。
将这类问题由易到难一一解决:
问题[1] 求无源汇的网络有上下界的可行流
由于下界是一条弧上的流必需要满足的确定值。下面引入必要弧的概念:必要弧是一定流要满的弧。必要弧的构造,将容量下界的限制分离开了,从而构造了一个没有下界的网络G’:
1. 将原弧(u,v)分离出一条必要弧: 。(红色表示)
。(红色表示)
2. 原弧: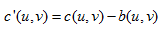 。
。
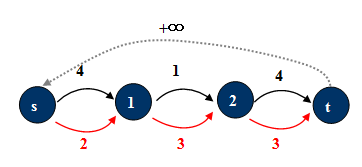
由于必要弧的有一定要满的限制,将必要弧“拉”出来集中考虑:

添加附加源x, 附加汇y。想像一条不限上界的(y, x),用必要弧将它们“串”起来,即对于有向必要弧(u, v),添加(u, y),(x, v),容量为必要弧容量。这样就建立了一个等价的网络。
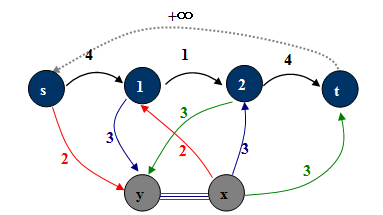
一个无源汇网络的可行流的方案一定是必要弧是满的。若去掉(y, x)后,附加源x到附加汇y的最大流,能使得x的出弧或者y的入弧都满,充要于原图有可行流。
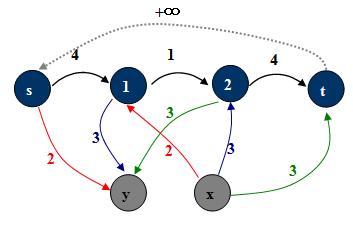
问题[2] 求无源汇的网络有上下界的可行流
算法:
1. 按上述方法构造新网络(分离必要弧,附加源汇)
2. 求附加源x到附加汇y的最大流
3. 若x的出弧或y的入弧都满,则有解,将必要弧合并回原图;否则,无解。
zoj2314(无源汇点 有上下界 可行流的判断)
代码:
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <queue>
const int MAXN =505;
const int MAXM=440020;
const int INF=0x3f3f3f3f;
using namespace std;
struct Edge {
int to,cap,flow,next;
} edge[MAXM];
int head[MAXN],tot,gap[MAXN],d[MAXN],cur[MAXN],que[MAXN],p[MAXN];
int n;
int id[MAXM];
void init()
{
tot=0;
memset(head,-1,sizeof(head));
}
void addedge(int u,int v,int c,int d)
{
edge[tot]=(Edge){v,c,0,head[u]};
id[d]= head[u] = tot++;
edge[tot]=(Edge){u,c,c,head[v]};
head[v] = tot++;
}
int isap(int source,int sink,int N)
{
memset(gap,0,sizeof(gap));
memset(d,0,sizeof(d));
memcpy(cur,head,sizeof(head));
int top = 0,x = source,flow = 0;
while(d[source] < N) {
if(x == sink) {
int Min = INF,inser=0;
for(int i = 0; i < top; ++i) {
if(Min > edge[p[i]].cap - edge[p[i]].flow) {
Min = edge[p[i]].cap - edge[p[i]].flow;
inser = i;
}
}
for(int i = 0; i < top; ++i) {
edge[p[i]].flow += Min;
edge[p[i]^1].flow -= Min;
}
if(Min!=INF) flow += Min;
top = inser;
x = edge[p[top]^1].to;
continue;
}
int ok = 0;
for(int i = cur[x]; i != -1; i = edge[i].next) {
int v = edge[i].to;
if(edge[i].cap > edge[i].flow && d[v]+1 == d[x]) {
ok = 1;
cur[x] = i;
p[top++] = i;
x = edge[i].to;
break;
}
}
if(!ok) {
int Min = N;
for(int i = head[x]; i != -1; i = edge[i].next) {
if(edge[i].cap > edge[i].flow && d[edge[i].to] < Min) {
Min = d[edge[i].to];
cur[x] = i;
}
}
if(--gap[d[x]] == 0) break;
gap[d[x] = Min+1]++;
if(x != source) x = edge[p[--top]^1].to;
}
}
return flow;
}
int main()
{
// freopen("in.txt","r",stdin);
int T,m,ss;
int a,b,low,up;
int d[MAXN];
int l[MAXM];
scanf("%d",&T);
while(T--)
{
init();
memset(d,0,sizeof(d));
ss=0;
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
{
scanf("%d%d%d%d",&a,&b,&low,&up);
addedge(a,b,up-low,i);
d[a]+=low;
d[b]-=low;
l[i]=low;
}
for(int i=1;i<=n;i++)
{
if(d[i]>0){
addedge(i,n+1,d[i],0);
ss+=d[i];
}
else
addedge(0,i,-d[i],0);
}
if(isap(0,n+1,n+2)==ss){
printf("YES\n");
for(int i=1;i<=m;i++) //最后输出可行流
printf("%d\n",edge[id[i]].flow+l[i]);
}
else
printf("NO\n");
}
return 0;
}
问题[2] 求有源汇的网络有上下界的可行流
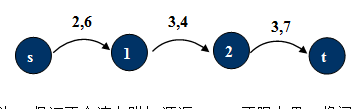
加入边(t, s),下界为0(保证不会连上附加源汇x, y),不限上界,将问题[2]转化为问题[1]来求解。
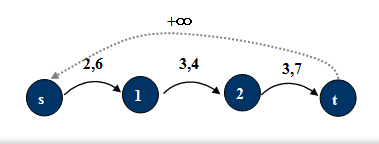
问题[3]求有源汇的网络有上下界的最大流
算法:
1. 先转化为问题[2]来求解一个可行流。若可行无解,则退出。由于必要弧是分离出来的,所以就可以把必要弧(附加源汇及其临边)及其上的流,暂时删去。再将(T,S)删去,恢复源汇。
2. 再次,从S到T找增广轨,求最大流。
3. 最后将暂时删去的下界信息恢复,合并到当前图中。输出解。
这样既不破坏下界(分离出来)也不超出上界(第2步满足容量限制),问题解决。
问题[4]求有源汇的网络有上下界的最小流
算法:
1. 同问题[3]。
2. 从T到S找增广轨,不断反着改进。
3. 同问题[3]。
问题[3]与问题[4]的另一种简易求法:
注意问题[2]中,构造出的(t, s),上下界几乎没什么限制。下面看看它的性质:
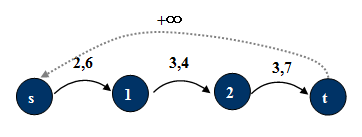
定理:如果从s到t有一个流量为a的可行流f,那么从t到s连一条弧(t, s),其流量下界b(t, s) = a,则这个图一定有一个无源汇的可行流:除了弧(t, s)的容量为a外,其余边的容量与f相同。
证明:如果从s到t的最大流量为amax,那么从t到s连一条下界b(t, s) = a’ > amax的弧(t, s),则从在这个改造后的图中一定没有无源汇的可行流:否则将这个可行流中的弧(t, s)除去,就得到了原图中s到t的流量为a’的流,大于最大流量amax,产生矛盾。
可以二分枚举这个参数a,即下界b(t, s),每次用问题[1]判断是否有可行流。这样就可以求出最大流。
同理,问题[4]要求最小流,只要二分枚举上界c(t, s)即可。
因为朴素的预流推进算法O(N3),总复杂度为O(N3 log2流量) 。
思路:
无源汇 (附加源汇+最大解决)
有源汇 (附加(T,S)->无源汇)



























 7137
7137

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








