C - Mike and gcd problem /* CodeForces - 798C */

C. Mike and gcd problem

time limit per test

 2 seconds

memory limit per test

 256 megabytes

input

 standard input

output

 standard output

Mike has a sequence A = [a1, a2, ..., an] of length n. He considers the sequence B = [b1, b2, ..., bn] beautiful if the gcd of all its elements is bigger than 1, i.e. .

Mike wants to change his sequence in order to make it beautiful. In one move he can choose an index i (1 ≤ i < n), delete numbersai, ai + 1 and put numbers ai - ai + 1, ai + ai + 1 in their place instead, in this order. He wants perform as few operations as possible. Find the minimal number of operations to make sequence A beautiful if it's possible, or tell him that it is impossible to do so.

 is the biggest non-negative number d such that d divides bi for every i (1 ≤ i ≤ n).

Input

The first line contains a single integer n (2 ≤ n ≤ 100 000) — length of sequence A.

The second line contains n space-separated integers a1, a2, ..., an (1 ≤ ai ≤ 109) — elements of sequence A.

Output

Output on the first line "YES" (without quotes) if it is possible to make sequence A beautiful by performing operations described above, and "NO" (without quotes) otherwise.

If the answer was "YES", output the minimal number of moves needed to make sequence A beautiful.

Examples

input

2
1 1

output

YES
1

input

3
6 2 4

output

YES
0

input

2
1 3

output

YES
1

Note

In the first example you can simply make one move to obtain sequence [0, 2] with .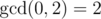

In the second example the gcd of the sequence is already greater than 1.

 

题意：给出一个序列 A ，我们可以将相邻两元素 a [ i ] , a [ i + 1 ] 改为 a [ i ] - a [ i + 1 ] 和 a [ i ] + a [ i + 1 ] ，问至少多少次操作后能使 gcd ( A1 ~ An) 大于1，若无法完成，则输出 NO

思路：显然我们把所有奇数修改成偶数即可满足条件，每次修改时若  a [ i ] 和 a [ i + 1 ] 同为奇数则修改一次，若一奇一偶则修改两次

 

 1 #include<bits/stdc++.h>  
 2 using namespace std;  
 3 const int N = 100000 + 10;  
 4   
 5 int n;  
 6 int a[N],c[N];  
 7   
 8 int gcd(int n,int m)  
 9 {  
10     int t = 1;  
11     while(t)  
12     {  
13         t=n%m;  
14         n=m;  
15         m=t;  
16     }  
17     return n;  
18 }  
19   
20 int main()  
21 {  
22     while(scanf("%d",&n)==1)  
23     {  
24         memset(c,0,sizeof(c));  
25         for(int i=0;i<n;i++)  
26         {  
27             scanf("%d",&a[i]);  
28         }  
29         int ans=0,tmp=gcd(a[0],a[1]);  
30         for(int i=0;i<n;i++)  
31         {  
32             tmp=gcd(tmp,a[i]);  
33             if(a[i]&1&&!c[i])  
34             {  
35                 if(a[i+1]&1) ans++;  
36                 else ans+=2;  
37                 c[i]=1;  
38                 c[i+1]=1;  
39             }  
40         }  
41         if(tmp!=1) printf("YES\n0\n");  
42         else printf("YES\n%d\n", ans);  
43     }  
44 }  

思维

 

From others. 

Thanks a lot.

转载于:https://www.cnblogs.com/xxQ-1999/p/7857857.html