【数据结构】——树状数组的几种模型

最新推荐文章于 2024-09-18 20:54:10 发布

MinecodeAir

最新推荐文章于 2024-09-18 20:54:10 发布

阅读量2.3k

点赞数 1

分类专栏： ▲—ACM—▲ ——算法学习笔记 ——数据结构文章标签：数据结构二进制 ACM

本文链接：https://blog.csdn.net/b735098742/article/details/52198579

版权

▲—ACM—▲ 同时被 3 个专栏收录

27 篇文章 0 订阅

订阅专栏

——数据结构

3 篇文章 0 订阅

订阅专栏

——算法学习笔记

1 篇文章 0 订阅

订阅专栏

转自我的个人博客(minecode.link)

树状数组

基本定义：树状数组是利用二分的思想使得查询和修改的复杂度都为log(n)的数据结构，主要用于查询数组前缀和、区间和并且经常更改数据。
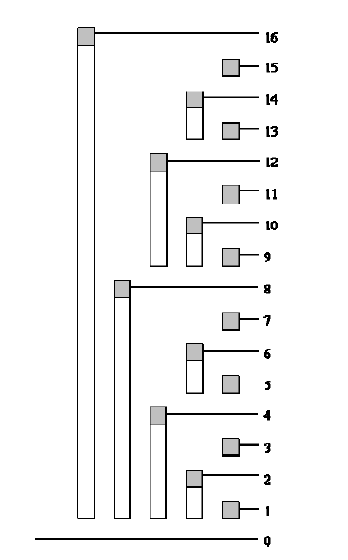
树状数组的存储方式

数据结构思想：如上图，2的k次方的位置存放1一直到 $2^k$ 这些数的和，然后再不断二分。具体实现可以用二进制解释，也就是例如XXX100中储存的是XXX000~XXX100这一个区间的所有数

基本操作：而要实现这一点，就要求一个二进制数的最低位1，这个可以用lowbit操作实现：
一个二进制数x对其进行x&(-x)的操作，就可以保留其最低位的1，而讲其他全部位全清零
所以一个数加上自己的lowbit，就到了上一级包含自己的区间，例如110(6)加上10变成了1000(8)，因为1000对应的0~1000
同样，减去自己的lowbit就相当于去尾。

模型1：改点求点求段

//设M为最大数的上限，treeray存树状数组
void add(int k,int num)//像某个位置添加的操作
{
    while(k<=M)//防止上界溢出
    {
        treeray[k]+=num;
        k+=k&(-k);//不断加上lowbit来向上更新包含自己的区间
    }
    return;
}

int read(int k)//读取以某个位置为终点的前缀和
{
    int sum=0;
    while(k)//一定要注意树状数组不能储存0这个位置
    {
        sum+=treeray[k];
        k-=k&(-k);//不断减lowbit来加上前面区间的和
    }
    return sum;
}

模型2：改段求点
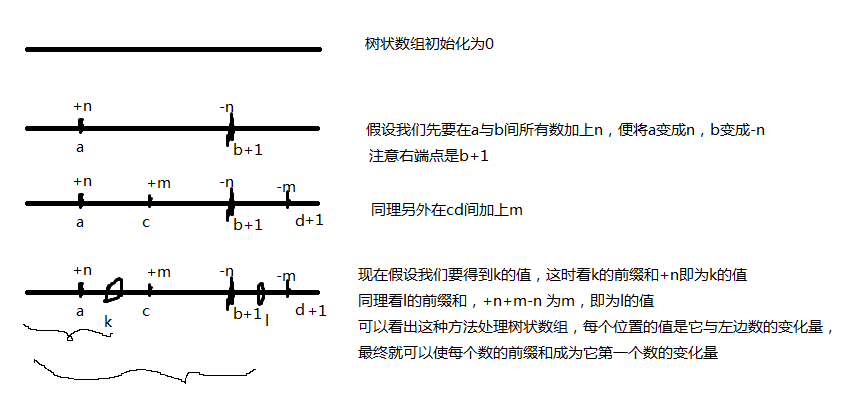
当需要改段求点时，利用树状数组方便求前缀和的特性，我们采用记录变化量的技巧，就可以使得一个数的前缀和变成他之前所有的变化量，便可得到这个数本身。
在树状数组中，每个数初始化为0，然后每个位置记录它与左边的差值，如图所示：

//add与read函数同上
//当在a与b间全部加上c时
add(a,c);
add(b+1,c);
//当要得到k的值时
read(k);

模型3：改段求段
当需要改段求段时，与前一种类型的区别是，需要求某一点“真正的”前缀和。考虑前一种方法，只知道该点本身与前面所有变化量的总和，却不知道这些变化是从哪里开始的，无法方便地求出前缀和。我们先假设这个点之前所有数都与这个点相等，这样必然会多出前面的一些变化值变化长度这么多，那么我们再用一个树状数组，其中在每一个变化点记录变化值变化长度，那么最终算某个点的和，只需要再减去这个树状数组的在该点的值，如图所示：

int A[],B[]; //两个树状数组
void tadd(int a[],int x,int c)
{
    while(x<=N)
    {
        a[x]+=c;
        x+=lowbit(x);
    }
    return;
}

int tread(int a[],int x)
{
    int sum=0;
    while(x>0)
    {
        sum+=a[x];
        x-=lowbit(x);
    }
    return sum;
}

void update(int a,int b,int c)
{
    tadd(A,a,c);
    tadd(A,b+1,-c);
    tadd(B,a,c*(a-1)); //叠加前缀变化量
    tadd(B,b+1,-c*b);
    return;
}

int querry(int a,int b)
{
    int sum1=tread(A,a-1)*(a-1)-tread(B,a-1);
    int sum2=tread(A,b)*b-tread(B,b);
    return sum2-sum1;
}

模型4：多维树状数组（以二维为例）
多维树状数组只需把多维的每一维度分别当作一维树状数组即可，那么N维的某一点的前缀和，其实就是，各个维度的前缀和分别映射到其他维度的前缀和
所以这里给出二维树状数组的代码实现，具体可以见下面的例题POJ1195：

void tadd(int i,int j,int c)
{
    for(int x=i;x<=N;x+=lowbit(x))
        for(int y=j;y<=N;y+=lowbit(y))//一定要注意这里不能再直接用传入的形参j了，因为每次循环都要使之成为刚传入的值
            base[x][y]+=c;
    return;
}

int tread(int i,int j)
{
    int sum=0;
    for(int x=i;x>0;x-=lowbit(x))
        for(int y=j;y>0;y-=lowbit(y))
            sum+=base[x][y];
    return sum;
}