【hihoCoder】第77周《Koch Snowflake》题目分析_koch雪花图形的形成过程为从一个等边三角形-CSDN博客

本文链接：https://blog.csdn.net/baidu_20163013/article/details/50382260

1、题目大意:

原题链接：http://hihocoder.com/contest/hiho77/problem/1

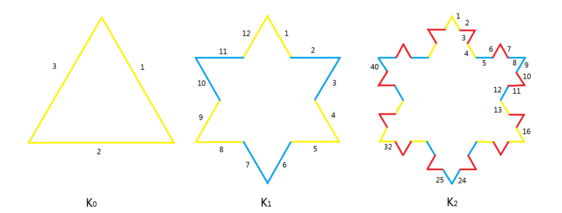
上图是著名的Koch雪花，或者叫Koch曲线。它是由一个等边三角形演变出来的。具体做法是——将每条边等分成三段，以中间一段为边长又形成一个等边三角形，再去掉中间那一段，就得到了上图所示的K1。然后无限重复这个过程。

Kn：第n次迭代生成的图形。(n=0,1,2,3….)；

Nn：Kn 边的数目，为 $3*4^n$ ；

S(i,n) : Kn的第i条边(i=1,2,3…Nn)；

给定S(i,n)，求这条边是第几代产生的。如上图，S(1,0)是第0代产生的；S(2,1)是第1代产生的；S(4,1)，也就是K1黄色那条边，是第0代产生的；S(9,2)，K2蓝色的边，是第1代产生的。

输入：
第一个数字(T<=1000)，表示测试案例个数，接下来有T行，每行两个数i(1<=i<= $10^9$ )和n(0<=n<=1000)。

输出：
T行，每行一个整数。

样例输入：

5
1 0
1 1
2 1
10 2
16 3

样例输出：

0
0
1
2
0

2、解题思路：

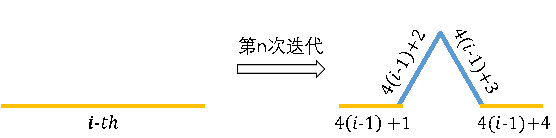
假设上图左边是第Kn-1的第i条边，经过一次变换得到Kn的4条边。由此得到两个个等式：
f(4(i-1)+1, n) = f(4(i-1)+4, n) = f(i,n-1)
f(4(i-1)+2, n) = f(4(i-1)+3, n) = n

代码如下：

int f(int i, int n){
    int x = i % 4;
    int y = ceil(i / 4);
    if (n == 0){
        return 0;
    }
    if (x == 2 || x == 3){
        return n;
    }
    else{
        return f(y, n-1);
    }
}

3、解题心得

类似这种题，一看应该是能找到数学规律的题目，可以巧解。但是在这之前我们应该先预先准备足够的测试用例，题目给的显然不够，我们可以自己先暴力多打印几组测试用例，就像下面的：

//-----------------------------------------------------
//All Rights Reserved, Copyright (C) 2015, beyourself
//-----------------------------------------------------
#include<iostream>
#include<cmath>
#include<vector>
using namespace std;

int f(int j, int n){...}

int main(){
    int i, j, k, n;
    vector<int> V[100];
    V[0].push_back(0);
    V[0].push_back(0);
    V[0].push_back(0);
    V[0].push_back(0);
    V[1].push_back(0);
    V[1].push_back(0);
    V[1].push_back(1);
    V[1].push_back(1);
    V[1].push_back(0);
    for (i = 2; i < 5; ++i){
        V[i].push_back(0);
        for (j = 1; j < V[i - 1].size(); ++j){
            for (k = 0; k < 4; ++k){
                if (k == 0 || k == 3){
                    V[i].push_back(V[i - 1][j]);
                }
                else{
                    V[i].push_back(i);
                }
            }//k
        }//j
    }//i


    int cas;
    cin >> cas;
    while (cas--){
        cin >> i >> n;

        int t = i % ((int)pow(4.0,n));
        if (t == 0){
            t = (int)pow(4.0, n);
        }
        if (V[n][t] == f(i, n)){
            cout << "\nRight!\n";
        }
        else{
            cout << "\nWrong!\n";
        }
    }//while
    return 0;
}