Level Set Evolution Without Re-initialization: A New Variational Formulation

Level Set Evolution Without Re-initialization: A New Variational Formulation

无重新初始化的水平集演化：新的变分公式

2.背景

2.1 传统的水平集方法

在活动轮廓的水平集公式中，用C来表示活动轮廓，水平集方程φ(t, x, y)用来表示零水平集C(t) = {(x, y)| φ(t, x, y) = 0}。水平集函数φ的演化方程可以用以下一般形式表示：

这被称为水平集方程[11]。 函数F称为速度函数。 对于图像分割，函数F取决于图像数据和水平集函数φ。
在传统的水平集方法中[5-7，17]，水平集函数φ在演化过程中会产生冲击，非常尖锐和/或平坦的形状，这使得进一步的计算非常不准确。 为了避免这些问题，一种常见的数值方案是在演化之前将函数φ初始化为有符号的距离函数，然后在进化过程中定期将函数φ“重塑”（或“重新初始化”）为有符号的距离函数。 确实，重新初始化过程至关重要，并且在使用传统水平集方法中无法避免[4-7]。

2.2 重新初始化的缺点

在传统的水平集方法中，重新初始化已被广泛用作数值补救方法[5-7]。标准的重新初始化方法是解以下重新初始化方程式

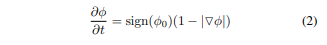
其中φ0是要重新初始化的函数，而sign（φ）是符号函数。 关于重新初始化方法已有大量文献[15，16]，其中大多数是上述基于PDE的方法的变体。 不幸的是，如果φ0不平滑或φ0在界面的一侧比另一侧陡峭，则所产生的函数φ的零水平集可能会从原始函数的零水平集中错误地移动[4、15、17]。 此外，当零水平集方程远离带符号的距离函数时，这些方法可能无法将水平集方程重新初始化为带符号的距离函数。 实际上，在少数迭代步骤中，尤其是在时间步长选择不足够小的情况下，不断发展的水平集方程可能会大大偏离其有符号距离的值。

3.无需重新初始化的曲线演化的可变水平集公式

3.1 具有变分能量的一般变化水平集公式

如前所述，至关重要的一点是，在演化过程中，尤其是在零水平集附近，保持进化水平集合函数为近似有符号距离函数。 众所周知，有符号距离函数必须满足|Oφ|的理想属性。|Oφ| =1。相反，满足|Oφ|的任何函数φ = 1是有符号距离函数加常数[19]。 当然，我们提出以下积分

作为一个度量来表征函数φ与Ω⊂R2中的有符号距离函数有多接近。 该指标将在我们的变分水平集制定中发挥关键作用。 利用上面定义的函数P（φ），我们提出以下变式

其中，μ> 0是一个参数，用于控制对φ与有符号距离函数的偏差进行补偿的效果，εm（φ）是确定的能量，它将驱动φ的零水平曲线的运动。
在本文中，我们用∂ε/∂φ表示泛函ε的Gateaux导数（或一阶变数）[18]，以及以下演化方程：

是使函数ε最小化的梯度流[18]。对于根据φ明确定义的特定函数ε（φ），可以根据函数φ及其导数[18]计算并表达Gateaux导数。
我们将专注于将（4）中的变分公式应用于活动轮廓进行图像分割，以便φ的零水平曲线可以演变为图像中所需的特征。 为此，将能量εm定义为依赖于图像数据的函数（请参见下文），因此我们将其称为外部能量。 因此，能量P（φ）被称为函数φ的内部能量，因为它仅是φ的函数。
在根据梯度流（5）使函数（4）最小化的过程中，零水平曲线将被外部能量εm移动。 同时，由于内部能量的惩罚作用，在演化过程中，根据演化（5），演化函数将自动保持为近似有符号距离函数。 因此，在提出的方法中完全消除了重新初始化过程。 接下来，将在活动轮廓中进一步说明该概念。

3.2 无需重新初始化的活动轮廓的变分水平集公式化

在图像分割中，活动轮廓是朝对象边界移动的动态曲线。 为了实现此目标，我们明确定义了一种外部能量，该能量可以将零水平曲线移向对象边界。 令I为图像，g为由以下项定义的边缘指示符函数：

其中Gσ是具有标准偏差σ的高斯核。 我们定义函数φ（x，y）的外部能量如下

其中λ> 0和ν是常数，而项Lg（φ）和Ag（φ）分别定义为

其中δ是单变量Dirac函数（冲激函数），H是Heaviside函数（阶跃函数）。 现在，我们定义以下总能量函数

外部能量Egλν驱使零水平集朝着物体边界移动，而内部能量µP（φ）则在演化过程中惩罚了φ与有符号距离函数的偏差。
为了更好的理解能量函数，我们假设零水平集φ表示为一个可微的参数化曲线C§，p∈[0,1]。我们已经知道[9]式（7）中能量函数在计算了零水平集曲线φ的零水平集曲线共形长度变化。另外式（8）中能量函数用来加速曲线演化。注意的是，当g函数的参数为1时，（8）中的能量函数为区域Ω-φ（曲线外区域）的面积[17]。可以将（8）中的能量函数Ag（φ）视为Ω-φ的加权区域。 Ag的系数ν可以为正也可以为负，具体取决于初始轮廓与感兴趣对象的相对位置。例如，如果初始轮廓放置在对象外部，则加权面积项中的系数ν应该取正值，以便轮廓可以更快地收缩。如果将初始轮廓放置在对象内部，则系数ν应该取负值，以加快轮廓的扩展速度。
通过微分计算[18]，可以将式（9）中的E的Gateaux导数（一阶变式）写为

其中M是拉普拉斯算子。 因此，使该函数最小化的函数φ满足Euler-Lagrange方程∂E/∂φ=0。使函数E最小化的最陡下降过程是以下梯度流：

该梯度流是所提出方法中水平集函数的演化方程。
（10）右侧的第二项和第三项分别对应于能量函数λLg（φ）和νAg（φ）的梯度流，并负责将零能级曲线推向物体边界。 为了解释与内部能量µP（φ）相关的第一项的影响，我们注意到了梯度流