Practical Pigment Mixing for Digital Painting文献简单翻译

一、背景

1. 研究背景

捷克科技大学的研究团队发表在2021年SIGGRAPH Asia上的研究成果，研究对象是在电子绘画软件上实现现实生活中颜料混合的效果。

在现实生活中，我们将蓝色和黄色的颜料混合会得到绿色，但如果使用电子绘画软件，如Photoshop、Procreate、Painter等，混合蓝色和黄色会得到偏灰的颜色，这是违反现实的。

该研究团队通过在常用的绘画软件中实现K-M模型，来在电子绘画领域实现现实生活中颜料混合的效果。

研究成果展示官网：https://scrtwpns.com/mixbox/
原论文地址：https://scrtwpns.com/mixbox.pdf
源代码地址：https://github.com/scrtwpns/pigment-mixing
视频展示地址：https://youtu.be/ATzVPVNp1qA （B站上有搬运）

2. 显示器的显色原理与现实生活中颜料显色的原理之不同

我们都知道主流的显示器都使用RGB三色显示，屏幕上的像素各自发出红、绿、蓝三种颜色的色光，三色光经过不同程度的混合呈现出不同的色彩。

但颜料的呈色原理与之截然不同。入射光照在一幅现实中的画作上时，光线在颜料内部经过这些颜料颗粒的吸收和散射，再反射出来进入人的眼睛。由于不同颜色的颜料对不同波长的光吸收和散射的能力不同，且每个色素颗粒都在各自进行吸收和散射，因此呈现出千差万别的颜色。

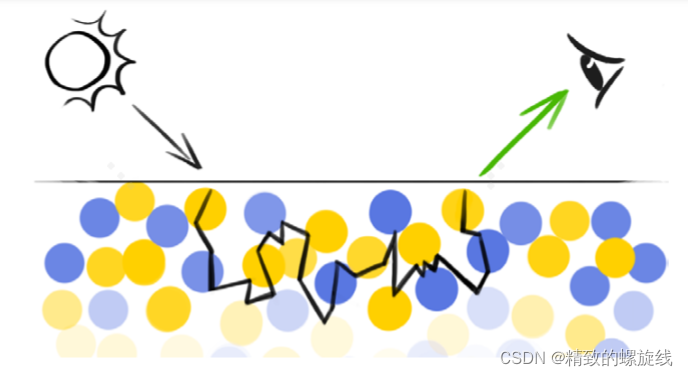
二、K-M模型

K-M模型用来计算入射光照在颜料上后得到的反射光的颜色。

1. 模型的缺陷

K-M模型在很早以前就被提出，为什么在数字绘画领域的软件几乎没有使用？

因为没有找到很好的实现K-M模型的方法。在当前的数字绘画软件上实现K-M模型，会遇到三个主要问题：

1. 主流绘画软件都采用RGB三通道模型，但K-M模型需要的通道数远远大于三个。
   在K-M模型中，和现实生活中调和颜料一样，每个像素的颜色都可以看作是由不同种基础颜色的颜料调和而来，因此K-M模型为每个像素都追踪产生这种颜色所需要的颜料和该颜料的浓度。或者，还有一种方法是追踪波长的吸收率和散射系数。但这两种方法都会大大增加每像素的通道数。
   由于大多数绘画软件都采用RGB三通道模型，增加每个像素的通道数就等于从底层上修改这些软件的颜色计算，这几乎是不可能实现的。

2. 计算量大。
   在屏幕上显示一幅画面需要计算每个像素的可见光积分，这项工作的计算量太大。

3. 颜料混合不能覆盖到RGB色域空间下的所有颜色。
   如果颜料混合方法得到的模型不能覆盖到RGB色域下的所有颜色，会增加两种模型之间相互转化的难度。RGB颜色表示的图像不能被颜料表示出来，会给图像在其他地方随意粘贴显示或再创造造成困难。

因此想要实现K-M模型，需要对症下药的解决这三个问题：

• 不再增加通道数，直接在RGB空间下实现K-M模型
• 令算法足够快，避免绘画时的延迟
• 让模型覆盖RGB整个色域，且避免颜色缺失或失真

2. 模型的数学原理

假设某块颜色对波长为$\lambda$的光线的吸收系数为$K(\lambda )$，散射系数为$S(\lambda )$。

假设该颜色由$N$种基础颜色的颜料粒子构成，每种颜料粒子的占的比重为$c_i(0\le i\le N)$，则该颜色可以用集合$\mathbf{c}=[c_1,...,c_N]$来表示($\sum _{i=1}^N{c}_i=1$且$c_i\ge 0$)。

则色彩$\mathbf{c}$在波长为$\lambda$的光照下的吸收系数$K_{mix}(\mathbf{c},\lambda )$和散射系数$S_{mix}(\mathbf{c},\lambda )$为

$$\begin{gathered} K_{mix}(\mathbf{c},\lambda )=\sum _{i=1}^N{c}_i{K}_i(\lambda ) \\ {S}_{mix}(\mathbf{c},\lambda )=\sum _{i=1}^N{c}_i{S}_i(\lambda ) \end{gathered}$$
得到的反射光为
$$R_{mix}(\mathbf{c},\lambda )=1+\frac{K_{mix}(\mathbf{c},\lambda )}{S_{mix}(\mathbf{c},\lambda )}-\sqrt{(\frac{K_{mix}(\mathbf{c},\lambda )}{S_{mix}(\mathbf{c},\lambda )}{)}^2+2\frac{K_{mix}(\mathbf{c},\lambda )}{S_{mix}(\mathbf{c},\lambda )}}$$

为了将$R_{mix}$显示到屏幕上，我们需要使用一种合适的光源照射该这个混合物，并计算反射光。这里我们使用CIE标准下的D65光源进行照射，D65标准光源是一种接近正午日光的光照，与sRGB色域中的白色色彩一致。

CIE标准同样规定了一种标准颜色空间CIE-XYZ，反射光线在XYZ空间下的坐标为
$$\begin{gathered} X(\mathbf{c})={\int }_{\lambda }\overline{x}(\lambda )D_{65}(\lambda )R_{mix}^{\prime }(\mathbf{c},\lambda )d\lambda \\ Y(\mathbf{c})={\int }_{\lambda }\overline{y}(\lambda )D_{65}(\lambda )R_{mix}^{\prime }(\mathbf{c},\lambda )d\lambda \\ Z(\mathbf{c})={\int }_{\lambda }\overline{z}(\lambda )D_{65}(\lambda )R_{mix}^{\prime }(\mathbf{c},\lambda )d\lambda \end{gathered}$$
（关于CIE-XYZ颜色空间的更多资料）

然后再将XYZ空间下的反射光颜色转换到RGB空间下。
$$\underset{\mathcal{P}}{\mathrm{mix}}(\mathbf{c})=\left[\begin{array}{c}R(\mathbf{c})\\ G(\mathbf{c})\\ B(\mathbf{c})\end{array}\right]=\frac{1}{Y_{D_{65}}}\left[\begin{array}{ccc}+3.2406& -1.5372& -0.4986\\ -0.9689& +1.8758& +0.0415\\ +0.0557& -0.2040& +1.0570\end{array}\right]\left[\begin{array}{c}X(\mathbf{c})\\ Y(\mathbf{c})\\ Z(\mathbf{c})\end{array}\right]$$

3. 模型的实现

当前绘画软件常用的混合两种颜色的办法是线性插值方法$lerp$，即
$$lerp(\mathbf{R}\mathbf{G}{\mathbf{B}}_1,\mathbf{R}\mathbf{G}{\mathbf{B}}_2,t)=(1-t)\mathbf{R}\mathbf{G}{\mathbf{B}}_1+t\mathbf{R}\mathbf{G}{\mathbf{B}}_2\text{s.t.}t\in [0,1]$$

我们的目标是找到另一种插值方法$kmerp$，要求它必须每一步都在RGB空间下实现k-m模型。

首先定义一组基础颜料 P ∗ = { ( K i ∗ ( λ ) , S i ∗ ( λ ) ) } i = 1 N \mathcal{P}^* = \{(K_i^*(\lambda), S_i^*(\lambda))\}_{i=1}^N P∗={(Ki∗​(λ),Si∗​(λ))}i=1N​，其他所有颜色都由这组基础颜料混合而来。这组基础颜料的颜色是在k-m计算前由用户自己定义好的。这里我们使用四个常见的有机颜料——酞青蓝、品红、汉萨黄、钛白，它们的混合可以提供非常广阔的色域。

首先将输入的RGB颜色分解成由这些基础颜色构成的颜色。这里使用最小二乘法，找到一组$\mathbf{c}$可以令这组$\mathbf{c}$混合出的颜色与给定的RGB颜色最相近。
$$\begin{gathered} \underset{{\mathcal{P}}^{\ast }}{\mathrm{unmix}}(\mathbf{R}\mathbf{G}\mathbf{B})=\underset{\mathbf{c}}{\mathrm{argmin}}||\underset{{\mathcal{P}}^{\ast }}{\mathrm{mix}}(\mathbf{c}-\mathbf{R}\mathbf{G}\mathbf{B})|{|}^2 \\ \text{s.t.}{c}_i\ge 0\wedge \sum _{i=1}^N{c}_i=1 \end{gathered}$$

尽管$mix$是在$\mathbf{c}$上是非线性的，但它是平滑且可微的，因此我们可以使用Newton-type solver来获得这个优化问题的解。

对于两个给定的颜色$\mathbf{R}\mathbf{G}{\mathbf{B}}_1$和$\mathbf{R}\mathbf{G}{\mathbf{B}}_2$，先将它们分解成${\mathbf{c}}_1$、${\mathbf{c}}_2$，然后使用线性相加计算混合后的颜色$\hat{\mathbf{c}}$，再转换成最后的RGB颜色。
$$\begin{gathered} {\mathbf{c}}_1=unmix(\mathbf{R}\mathbf{G}{\mathbf{B}}_1) \\ {\mathbf{c}}_2=unmix(\mathbf{R}\mathbf{G}{\mathbf{B}}_2) \\ \hat{\mathbf{c}}=(1-t){\mathbf{c}}_1+t{\mathbf{c}}_2 \\ kmerp(\mathbf{R}\mathbf{G}{\mathbf{B}}_1,\mathbf{R}\mathbf{G}{\mathbf{B}}_2,t)=mix(\hat{\mathbf{c}}) \end{gathered}$$

4. 覆盖全部RGB色域

上述的转换方法有一个不足，就是我们前面提到过的，使用颜料混合的方法无法覆盖到RGB色彩空间的全部色域。事实上，RGB空间中有一些颜色是无法被已知的任何一种颜料混合出来的，这些颜色只能由自发光产生。这类颜色是无法通过$mix$函数计算得到的。同时这也会导致另一个问题，当$t=0$或$t=1$时，无法保证得到的混合颜色能再现输入的颜色。

RGB色域下的颜色是由红、绿、蓝三种颜色的色光混合形成的，而颜料产生的颜色是光线经由颜料粒子的吸收和散射后反射得到的，因此相比本身的RGB色域，颜料反射得到的颜色必然有缺失。因此我们引入一个残差项，来弥补这种缺失，即
$$\mathbf{r}=\mathbf{R}\mathbf{G}\mathbf{B}-mix(unmix(\mathbf{R}\mathbf{G}\mathbf{B}))$$

因为这个残差项本身代表的是光，所以也符合线性规则，可以将它们引入到前面的线性混合公式中，得到修正后的kmerp
$$\begin{gathered} {\mathbf{c}}_1=unmix(\mathbf{R}\mathbf{G}{\mathbf{B}}_1),{\mathbf{r}}_1=\mathbf{R}\mathbf{G}{\mathbf{B}}_1-mix({\mathbf{c}}_1) \\ {\mathbf{c}}_2=unmix(\mathbf{R}\mathbf{G}{\mathbf{B}}_2),{\mathbf{r}}_2=\mathbf{R}\mathbf{G}{\mathbf{B}}_2-mix({\mathbf{c}}_2) \\ \hat{\mathbf{c}}=(1-t){\mathbf{c}}_1+t{\mathbf{c}}_2 \\ \hat{\mathbf{r}}=(1-t){\mathbf{r}}_1+t{\mathbf{r}}_2 \\ kmerp(\mathbf{R}\mathbf{G}{\mathbf{B}}_1,\mathbf{R}\mathbf{G}{\mathbf{B}}_2,t)=mix(\hat{\mathbf{c}})+\hat{\mathbf{r}} \end{gathered}$$

因为在kmerp的计算中，$\mathbf{c}$和$\mathbf{r}$的计算方式是相同的，因此我们使用一个把$\mathbf{c}$和$\mathbf{r}$齐次连接在一起，得到一个向量
$$\mathbf{z}={\left[\begin{array}{ccccccc}{c}_1& c_2& c_3& c_4& r_R& r_G& r_B\end{array}\right]}^{\mathrm{T}}$$

用$\mathcal{F}$表示将$\mathbf{R}\mathbf{G}\mathbf{B}$转换成该向量，$\mathcal{G}$表示转换回来，则有
$$\begin{gathered} \mathcal{F}(\mathbf{R}\mathbf{G}\mathbf{B})=\left[\begin{array}{c}\mathbf{c}\\ \mathbf{r}\end{array}\right]=\left[\begin{array}{c}unmix(\mathbf{R}\mathbf{G}\mathbf{B})\\ \mathbf{R}\mathbf{G}\mathbf{B}-mix(\mathbf{c})\end{array}\right]=\mathbf{z} \\ \mathcal{G}(\mathbf{z})=\mathcal{G}\left(\left[\begin{array}{c}\mathbf{c}\\ \mathbf{r}\end{array}\right]\right)=mix(\mathbf{c})+\mathbf{r} \end{gathered}$$

因此，两个RGB颜色混合的过程可以写成
$$kmerp(\mathbf{R}\mathbf{G}{\mathbf{B}}_1,\mathbf{R}\mathbf{G}{\mathbf{B}}_2,t)=\mathcal{G}((1-t)\mathcal{F}(\mathbf{R}\mathbf{G}{\mathbf{B}}_1)+t\mathcal{F}(\mathbf{R}\mathbf{G}{\mathbf{B}}_2))$$

这种算法既可以覆盖到RGB空间下所有颜色，也可以保证输入和输出都是RGB模式，满足各类软件的需要。

混合超过两种颜色时，可以使用加权平均的方法表示$n$种颜色的混合
$$\mathcal{G}\left(\frac{{\sum }_{i=1}^n{w}_i\mathcal{F}({\mathbf{R}\mathbf{G}\mathbf{B}}_i)}{{\sum }_{i=1}^n{w}_i}\right)$$

解决RGB色域不能完全覆盖颜料颜色的问题
除了颜料颜色不能完全覆盖RGB色域外，RGB色域也不能完全覆盖颜料调出的颜色。如下图，一些颜色超出了RGB色域，我们要想办法解决这个问题。

文章的作者想出三种办法解决这个问题。

第一种方法是直接将超出色域的部分暴力裁剪掉。这种方法带来的问题是这种计算是不可逆的，如果原始的颜料经过多次混合，那么在多次混合和裁剪操作后会对颜色数据造成很大的损失。

第二种方法是对颜料的色域进行压缩使之能完美符合RGB色域方块的范围。由于压缩解压缩过程是双向可逆的，因此不会造成颜色损失，但经过作者的多次实验，发现常用的色域压缩算法都会对颜色造成较大的偏移，因此放弃。

第三种方法是不再对颜料混合后得到的最终色彩进行变形，而是直接对输入的基础颜料进行变形，使之满足它们的混合物一定处于RGB色域方块内。前文中我们将基础颜色标记为${\mathcal{P}}^{\ast }$，这里我们将变形后的基础颜料颜色标记为${\mathcal{Q}}^{\ast }$，则${\mathcal{Q}}^{\ast }$的求解方法为
$$\begin{gathered} \underset{\mathcal{Q}}{\mathrm{argmin}}{E}_{push}(\mathcal{Q})+\alpha E_{pull}(\mathcal{Q},{\mathcal{P}}^{\ast })(\ast ) \\ \text{s.t.}K(\lambda )>0\wedge S(\lambda )>0\forall (K,S)\in \mathcal{Q} \end{gathered}$$

这里，$\mathcal{Q}$表示四个变形后基础颜料的光线吸收系数和散射系数构成的集合 Q = { ( K i † ( λ ) , S i † ( λ ) ) } i = 1 4 \mathcal{Q}=\{(K_i^\dagger(\lambda), S_i^\dagger(\lambda))\}_{i=1}^4 Q={(Ki†​(λ),Si†​(λ))}i=14​。

集合$\mathcal{Q}$中所有颜色的混合构成了色域空间$\Omega$，为了让$\Omega$完全处于RGB方块内部，且对${\mathcal{P}}^{\ast }$的变化尽可能小，我们引入$E_{push}$来惩罚$\Omega$集合的边界中超过RGB方块的部分。因此有
$$E_{push}(\mathcal{Q})={\int }_{\partial \Omega }\max (0,\varphi (\underset{\mathcal{Q}}{\mathrm{mix}}(c)){)}^2\text{d}s$$
其中$\text{d}s$表示$\Omega$集合的边界，$\varphi (\mathbf{p})$表示点$\mathbf{p}$到单位立方体$[0,1{]}^3$的表面上最近的一个点的有符号距离，$\mathbf{p}$在立方体外时为正，在立方体内部时为负。

此外，我们还引入$E_{pull}$来惩罚由$\mathcal{Q}$混合得到的颜色和由${\mathcal{P}}^{\ast }$混合得到的颜色之间的差异。
$$E_{pull}(\mathcal{Q},{\mathcal{P}}^{\ast })={\int }_{\partial \Omega }||\psi (\underset{\mathcal{Q}}{\mathrm{mix}}(c))-\psi (\underset{{\mathcal{P}}^{\ast }}{\mathrm{mix}}(c))|{|}^2\text{d}s$$
为了让${\mathcal{Q}}^{\ast }$和${\mathcal{P}}^{\ast }$在视觉上的差异尽可能小，我们将RGB颜色通通转换到Oklab色彩空间下进行计算，函数$\psi$就是完成RGB到Oklab的转换计算。

参数$\alpha$用来控制push和pull的强度。为了获取最佳的${\mathcal{Q}}^{\ast }$，我们设置初始值$\alpha =10^5$，${\mathcal{Q}}^0={\mathcal{P}}^{\ast }$，重复解优化问题(*)，每一步都让$\alpha$减半。一旦满足色域$\Omega$刚好符合RGB方块的大小则停止迭代。

$E_{push}$和$E_{pull}$两个积分的计算时通过在颜料色域空间的边界$\partial \Omega$上等间距的采样一系列正交点计算的。我们通过自动微分获得目标的梯度，并使用L-BFGS-B算法在循环中进行求解。

三、代码实现

代码实现主要完成以下三个步骤：

1. 将每个参与计算的RGB颜色编码成向量$\mathbf{z}$
2. 计算所有向量的加权平均值
3. 将结果向量解码回RGB颜色

为了提高$\mathcal{F}$和$\mathcal{G}$的计算速度，作者建立了查找表并进行大量的提前计算。提前计算的过程是：首先选取一系列基础颜料${\mathcal{P}}^{\ast }$，从现有的数据库中获取颜料的吸收系数$K(\lambda )$、散射系数$S(\lambda )$和反射率常量$k_1$、$k_2$。

编码过程$\mathcal{F}$中的$unmix$函数需要的计算量较大，因为它需要对每个输入的RGB像素都使用类牛顿求解器(quasi-Newton solver)。我们设置未混合颜料的初始浓度为${\mathbf{c}}^0=(0.25,0.25,0.25,0.25)$，使用L-BFGS-B算法并自动微分，这个过程大约需要100ms达到收敛。我们可以提前计算好所有8-bit的RGB颜色的$unmix$函数结果，并存储在一张三维查找表中。四种基础颜料的浓度实际上只需要保存三个，因为$c_4=1-(c_1+c_2+c_3)$。8bit的RGB能表示$256^3$个颜色，因此查找表有$256^3$行，总共占用48MB空间。

建立第二个查找表用于存储提前计算好的$mix$函数的结果。$mix$函数中最复杂的是计算三色积分$X(\mathbf{c})$、$Y(\mathbf{c})$、$Z(\mathbf{c})$，我们将计算结果也存储在一个48MB大小的$256^3$行表中。

继续减少两张查找表的占用空间，可以将它们分别压缩成两张4096×4096大小的PNG图片，两张图片总共占用7MB空间，完全可以打包进绘画软件中。

基础颜料的选择

使用不同颜色的基础颜料，会造成调色结果拥有不同的色相。我们的算法使用到四个基础颜料，我们允许用户自由选择三种颜色，最后一个颜色保留为白色。通常会推荐用户选择从红色、黄色、蓝色中各选一种。

此外，使用不同的纸张媒介也会造成不同的色彩结果，因为媒介会影响颜料的吸收系数和散射系数。

截止目前，该算法已经在Rebelle软件上实装，有兴趣的可以试试。论文剩下的内容就是对算法效果的评估了，此处不再翻译，有兴趣的自己看吧……