图像增强—空域平滑

图像噪声

图像噪声是指图像在摄取或传输过程中所受到的随机干扰信号，通常分为内部噪声和外部噪声
在图像处理过程中通常会接触到三类噪声：

• 椒盐噪声：含有随机出现的黑白强度值，通常呈点状，不形成大的连通域
• 脉冲噪声：只含有随机的白强度(正脉冲)噪声或黑强度(负脉冲)噪声
• 高斯噪声：含有强度服从高斯分布的噪声

图像平滑

图像平滑的目的是改善图像质量，尽量消除噪声对图像带来的影响。其本质是低通滤波。

图像的空域平滑实现起来很简单，将原图中的每一个点的灰度与它周围点的灰度进行加权和平均，作为新图中对应点的灰度，就能实现滤波的效果。若噪声是随机独立分布的，利用邻域平均或加权平均可以有效抑制噪声干扰

平滑模板(template)

平滑模板操作实现了一种邻域运算(Neighborhood Operation)，即某个像素点的结果灰度与其邻域点有关，模板运算的数学涵义是一种卷积(互相关)运算。平滑模板用邻域点的均值代替该中心元素的原值从而去除突然变化的点，滤掉噪声，其代价是图像会呈现一定程度的模糊。

由于模板要用到中心元素的邻域元素，因此通常不被允许移出图像边界，所以模板处理后的图像会比原图小。为了防止处理后的图像变小的情况，通常会复制原图灰度到无法进行模板处理的点，不进行其他处理；或者先扩大原图边界再进行模板处理

Box模板：将图像中每一个点的灰度与它周围八个点的灰度和进行平均
$$T^3=\frac{1}{9}\left[\begin{array}{ccc}1& 1& 1\\ 1& 1_{.}& 1\\ 1& 1& 1\end{array}\right]$$Box模板中的$1_{.}$表示该元素为中心元素，以该元素为基点进行运算

拟合圆的Box模板$$T_c^3=\frac{1}{21}\left[\begin{array}{ccccc}0& 1& 1& 1& 0\\ 1& 1& 1& 1& 1\\ 1& 1& 1.& 1& 1\\ 1& 1& 1& 1& 1\\ 0& 1& 1& 1& 0\end{array}\right]$$

Box模板应用举例：
设一图像为$f=\left[\begin{array}{cccc}2& 2& 2& 2\\ 3& 2& 3& 3\\ 4& 6& 4& 5\\ 5& 6& 6& 6\end{array}\right]$，对其应用$T^3$的Box模板，得到：$$F=\left[\begin{array}{cccc}2& 2& 2& 2\\ 3& 3.11& 3.22& 3\\ 4& 4.33& 4.56& 5\\ 5& 6& 6& 6\end{array}\right]$$

高斯模板
Box模板没有考虑各点位置的影响，对周围点没有权值变化，通常情况下平滑效果并不理想

因此考虑使用高斯平滑模板，高斯平滑模板通过采样二维高斯函数得到，引入加权系数，离中心像素越近的点对该点的影响越大权值越高

二维高斯函数：

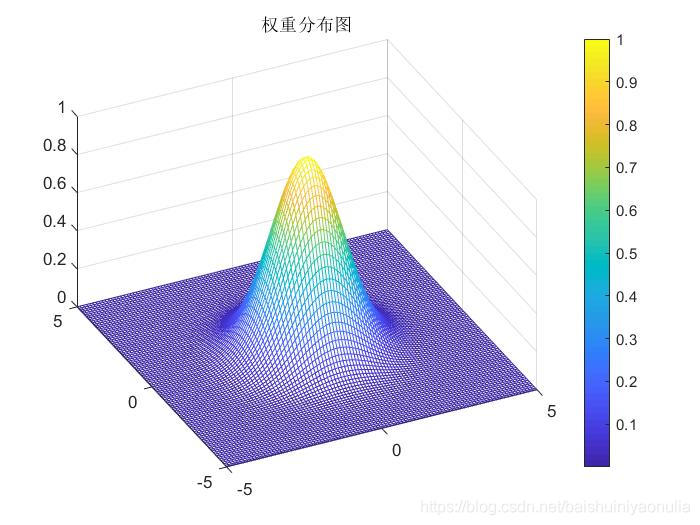
一个典型的高斯平滑模板：$$H_3=\frac{1}{16}\left[\begin{array}{ccc}1& 2& 1\\ 2& 4_{.}& 2\\ 1& 2& 1\end{array}\right]$$

高斯模板应用举例：
设一图像为$f=\left[\begin{array}{cccc}2& 2& 2& 2\\ 3& 2& 3& 3\\ 4& 6& 4& 5\\ 5& 6& 6& 6\end{array}\right]$，对其应用高斯模板，得到：$$F=\left[\begin{array}{cccc}2& 2& 2& 2\\ 3& 3& 3.06& 3\\ 4& 4.56& 4.56& 5\\ 5& 6& 6& 6\end{array}\right]$$

中值滤波—非线性滤波
中值滤波是指把以某点$(x,y)$为中心的小窗口内的所有像素的灰度从小到大排列，将中间值作为$(x,y)$处的灰度值，通常滤波窗口覆盖的元素数量取奇数，若窗口中有偶数个像素则取两个中间值的平均。

中值滤波器也是一种典型的低通滤波器，它在去除孤立噪声的同时能很好的保护图像边界，但对密集噪声和高斯噪声作用不大

例如下面矩阵中的6即为一个孤立的噪声点，经过一个3*1的中值滤波窗口处理后被平滑为1，同时图像边界保存完好，不像Box模板和高斯模板一样会使边界模糊
$$\left[\begin{array}{ccccccc}0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 1& 1& 1& 0& 0\\ 0& 0& 1& 6& 1& 0& 0\\ 0& 0& 1& 1& 1& 0& 0\\ 0& 0& 0& 0& 0& 0& 0\end{array}\right]\to \square \square \square \to \left[\begin{array}{ccccccc}0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 1& 1& 1& 0& 0\\ 0& 0& 1& 1& 1& 0& 0\\ 0& 0& 1& 1& 1& 0& 0\\ 0& 0& 0& 0& 0& 0& 0\end{array}\right]$$