1.1
数据:所有可以输入到计算机中的内容
数据元素:数据的基本单位,数据库中表的项
数据对象:性质相同的数据元素的集合,整数数据对象的集合N={0,+/-1,+/-2,...}
数据结构:数据对象+数据元素的关系
存储结构:数据结构在计算机内存中的映像
数据类型:基本数据类型,自定义数据类型+数据操作
抽象数据类型:数据结构+操作
1.2
数据结构:数据对象(程序设计语言中的基本类型+自定义类型)+关系(程序设计语言中顺序存储关系数组,链式关系指针)
抽象数据类型:数据结构+操作
程序设计语言中的数据类型:基本数据类型+自定义数据类型
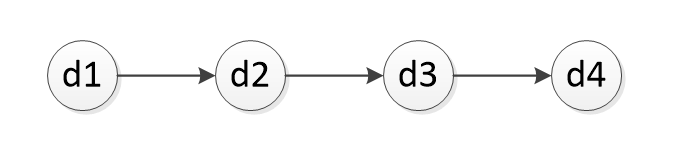
1.3 D={d1,d2,d3,d4},R={r},r={(d1,d2),(d2,d3),(d3,d4)}
该数据结构的逻辑图为
1.4抽象数据类型复数和有理数的表示
复数:
ADT Complex{
数据对象:D={r,i|r,i为实数}
数据关系:R={<r,i>}
基本操作:
InitComplex(&C,re,im)
操作结果:构造一个复数C,其实部和虚部分别为re和im
DestroyCmoplex(&C)
操作结果:销毁复数C
Get(C,k,&e)
操作结果:用e返回复数C的第k元的值
Put(&C,k,e)
操作结果:改变复数C的第k元的值为e
IsAscending(C)
操作结果:如果复数C的两个元素按升序排列,则返回1,否则返回0
IsDescending(C)
操作结果:如果复数C的两个元素按降序排列,则返回1,否则返回0
Max(C,&e)
操作结果:用e返回复数C的两个元素中值较大的一个
Min(C,&e)
操作结果:用e返回复数C的两个元素中值较小的一个
}ADT Complex
有理数:
ADT RationalNumber{
数据对象:D={r1,r2|r1,r2属于自然数且不为0}
数据关系:R={<s,m>}
基本操作:
InitRationalNumber(&R,s,m)
操作结果:构造一个有理数R,其分子和分母分别为s和m
DestroyRationalNumber(&R)
操作结果:销毁有理数R
Get(R,k,&e)
操作结果:用e返回有理数R的第k元的值
Put(&R,k,e)
操作结果:改变有理数R的第k元的值为e
IsAscending(R)
操作结果:若有理数R的两个元素按升序排列,则返回1,否则返回0
IsDescending(R)
操作结果:若有理数R的两个元素按降序排列,则返回1,否则返回0
Max(R,&e)
操作结果:用e返回有理数R的两个元素中值较大的一个
Min(R,&e)
}ADT RationalNumber
1.5画程序流程图
<span style="font-size:18px;"><span style="font-size:18px;color:#000000;">product=1,i=1;
while(i<=n){
product *= i;
i++;
}</span></span>计算n的阶乘
<span style="font-size:18px;"><span style="font-size:18px;color:#000000;">i=0;
do{
i++;
}while((i!=n) && (a[i]!=x));</span></span>在向量中查找值为x的位置
<span style="font-size:18px;"><span style="font-size:18px;color:#000000;">switch{
case x<y:z=y-x;break;
case x==y:z=abs(x*y);break;
default:z=(x-y)/abs(x)*abs(y);
}</span></span>分支结构
1.6
(1)exit常用于异常错误处理,它可以强行中断程序的执行,返回操作系统。
(2)以函数的返回值判断正确与否常用于子程序的测试,便于实现程序的局部控制。
(3)用整型变量进行错误处理的优点是可以给出错误类型,便于迅速确定错误。
1.7
(1)用scanf和printf直接进行输入输出的好处是形象、直观,但缺点是需要对其进行格式控制,较为烦琐,如果出现错误,则会引起整个系统的崩溃。
(2)通过函数的参数传递进行输入输出,便于实现信息的隐蔽,减少出错的可能。
(3)通过全局变量的隐式传递进行输入输出最为方便,只需修改变量的值即可,但过多的全局变量使程序的维护较为困难。
1.8
(1)n-1
(2)n-1
(3)n-1
(4)等差数列前n项和 n(a1+an)/2=n(1+n)/2
(5)(1/2)*(1/6)*n*(n+1)*(2n+1)+(1/2)*n*(n+1)=(1/12)n(n+1)(2n+4)
(6)n 以n=10为例
<span style="font-size:18px;">clear all
close all
clc
n = 0:1:10;
plot(n,n,'-k',...
'LineWidth',2);
hold on;
plot(n,10-n,'-r',...
'LineWidth',2);
hold on;
x = [1,1,2,2,3,3,4,4,5,5];
y = [0,1,1,2,2,3,3,4,4,5];
plot(x,y,'o',...
'MarkerSize',10,...
'MarkerEdgeColor','b',...
'MarkerFaceColor',[0,0,1]);
grid on;
</span>
(7)小于等于(sqrt(y)-1)的最大整数
(8) 1100
1.9 count = log2n-2,复杂度 o(log2(n))
1.10
1.11 n^10 <= 10^12 ,n<=exp(1.2*ln10)
2^n <= 10^12,n<=12*ln10/ln2
1.12 f(n) = o(n4) ,g(n) = o(n4),h(n)=o(n3.5)
1.13 编程计算
1.14 < < > >
1.15(1)高中数列公式(2)等比数列求和(3)等比数列求和(4)等差数列求和
1.17计算fibonacci数列
动态规划策略:从递归基出发,自底而上递推地得出各子问题的解,直至最终原问题的解
n p=fib(n-1) fib(n-2) q=fib(n)
0 1 -1 0 递归基
1 0 1 1
2 1 0 1
3 1 1 2
4 2 1 3
初始p=1 q=0,
每次迭代 q = p+q;
p = q-p;
//返回第m个fibonacci数
int fib(int m)
{
int p = 1;//递归基
int q = 0;//递归基
while(m-- >= 0)
{
q = p+q;
p = q-p;
}
return q;
}





















 987
987











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








