poj 1459 Power Network (网络最大流)

Description

A power network consists of nodes (power stations, consumers and dispatchers) connected by power transport lines. A node u may be supplied with an amount s(u) >= 0 of power, may produce an amount 0 <= p(u) <= p _max(u) of power, may consume an amount 0 <= c(u) <= min(s(u),c _max(u)) of power, and may deliver an amount d(u)=s(u)+p(u)-c(u) of power. The following restrictions apply: c(u)=0 for any power station, p(u)=0 for any consumer, and p(u)=c(u)=0 for any dispatcher. There is at most one power transport line (u,v) from a node u to a node v in the net; it transports an amount 0 <= l(u,v) <= l _max(u,v) of power delivered by u to v. Let Con=Σ _uc(u) be the power consumed in the net. The problem is to compute the maximum value of Con.

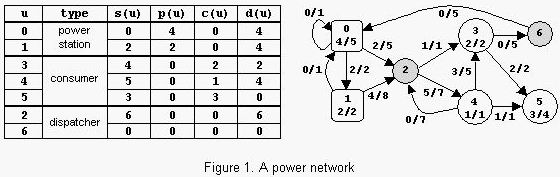
An example is in figure 1. The label x/y of power station u shows that p(u)=x and p _max(u)=y. The label x/y of consumer u shows that c(u)=x and c _max(u)=y. The label x/y of power transport line (u,v) shows that l(u,v)=x and l _max(u,v)=y. The power consumed is Con=6. Notice that there are other possible states of the network but the value of Con cannot exceed 6.

Input

There are several data sets in the input. Each data set encodes a power network. It starts with four integers: 0 <= n <= 100 (nodes), 0 <= np <= n (power stations), 0 <= nc <= n (consumers), and 0 <= m <= n^2 (power transport lines). Follow m data triplets (u,v)z, where u and v are node identifiers (starting from 0) and 0 <= z <= 1000 is the value of l _max(u,v). Follow np doublets (u)z, where u is the identifier of a power station and 0 <= z <= 10000 is the value of p _max(u). The data set ends with nc doublets (u)z, where u is the identifier of a consumer and 0 <= z <= 10000 is the value of c _max(u). All input numbers are integers. Except the (u,v)z triplets and the (u)z doublets, which do not contain white spaces, white spaces can occur freely in input. Input data terminate with an end of file and are correct.

Output

For each data set from the input, the program prints on the standard output the maximum amount of power that can be consumed in the corresponding network. Each result has an integral value and is printed from the beginning of a separate line.

Sample Input

2 1 1 2 (0,1)20 (1,0)10 (0)15 (1)20
7 2 3 13 (0,0)1 (0,1)2 (0,2)5 (1,0)1 (1,2)8 (2,3)1 (2,4)7
         (3,5)2 (3,6)5 (4,2)7 (4,3)5 (4,5)1 (6,0)5
         (0)5 (1)2 (3)2 (4)1 (5)4

Sample Output

15
6

Hint

The sample input contains two data sets. The first data set encodes a network with 2 nodes, power station 0 with pmax(0)=15 and consumer 1 with cmax(1)=20, and 2 power transport lines with lmax(0,1)=20 and lmax(1,0)=10. The maximum value of Con is 15. The second data set encodes the network from figure 1.

 

采用网络流的模型来解决，在原图的基础上添加一个源点s和汇点t，对于每个发电站，从源点s引一条容量为pmax的弧；对于每个用电场所，引一条容量为cmax的弧到汇点t。

对于三元组（u，v，z），从u引一条容量为z的弧到v，最大电力消耗con就是这个网络的最大流。

采用相邻矩阵来存储网络中的流量（f[n][n]）和容量（c[n][n]），采用BFS算法求增广路径时需要用一个队列q[n]和记录增广路径的数组fa[n]，n是指网路中的节点个数，fa[i]为增广路径上节点i的前驱。

 

#include <iostream>
#include <stdio.h>
#include <cmath>
#include <string.h>
#include <queue>
using namespace std;
int n,np,nc,m,s,t;
int fa[104],f[104][104],c[104][104];
//fa[j]存储增广路径，为节点j在增广路径上的前驱节点，正数表示该弧为前向弧，负数表示该弧为后向弧
//f[][],c[][]记录网路中的流量和容量，存储方式为相邻矩阵
void pro()
{
    int i,j,d,d0,ans=0;
    fa[t]=1;   //汇点的前驱指针初始化
    while(fa[t]!=0)  //如果增广路径存在
    {
        queue<int> q;  //定义队列
        q.push(s);  //源点进入队尾
        memset(fa,0,sizeof(fa));  //增广路径初始化
        fa[s]=s; //源点的前驱指针指向自己
        while((!q.empty())&&(fa[t]==0)) //如果队列非空并且没有找到至汇点的增广路径
        {
            i=q.front(); q.pop(); //取出队首节点
            for(j=1;j<=t;j++)  //枚举未在增广路径上的节点j
                if(fa[j]==0)
                 if(f[i][j]<c[i][j]) //如果(i,j)的流量可增加，则(i,j)作为前向弧加入增广路径，j进入队列
                 {
                    fa[j]=i;
                    q.push(j);
                 }
                 else if(f[j][i]>0)//如果(i,j)可退流，则（i,j）作为后向弧加入增广路径，j进入队列
                 {
                     fa[j]=-i;
                     q.push(j);
                 }
        }
        if(fa[t]!=0)//如果找到一条从源点到汇点增广路径就改进当前流
        {
            d0=99999999;
            i=t; //从汇点出发倒推计算最大可改进量d0
            while(i!=s) //还没有倒推至源点
            {
                if(fa[i]>0) //i节点为尾的弧是前向弧
                  {if((d=c[fa[i]][i]-f[fa[i]][i])<d0)
                    d0=d;
                  }
                else if(f[i][-fa[i]]<d0)//i节点为尾的弧是后向弧
                    d0=f[i][-fa[i]];
                i=abs(fa[i]);//继续沿前驱指针倒推计算最大可改进量d0
            }
            ans=ans+d0; //总流量增加d0
            i=t;  //从汇点出发倒推调整增广路径上的流量
            while(i!=s)
            {
                if(fa[i]>0) //若i节点为尾的弧是前向弧，则该弧流量增加d0
                    f[fa[i]][i]+=d0;
                else
                    f[i][-fa[i]]-=d0;//若i节点为尾的弧是后向弧，则该弧流量减少d0
                i=abs(fa[i]); //继续沿前驱指针调整流量
            }
        }
    }
    cout<<ans<<endl;//输出最大流
}
int main()
{
    int i,u,v,cc;
    while(cin>>n>>np>>nc>>m)//反复输入节点数，发电站数目，用电场所数目，电力传输线数目
    {
        s=n+2;t=n+1;  //设置源点s和汇点t
        memset(f,0,sizeof(f));
        memset(c,0,sizeof(c));
        for(i=1;i<=m;i++)  //对于原图中的边（u，v）连一条容量是cc的弧
        {
            while(getchar()!='(');
            scanf("%d,%d)%d",&u,&v,&cc);
            c[u+1][v+1]=cc;
        }
        for(i=1;i<=np;i++)  //源点向每一个发电站连一条容量是cc的弧
        {
            while(getchar()!='(');
            scanf("%d)%d",&u,&cc);
            c[s][u+1]=cc;
        }
        for(i=1;i<=nc;i++) //每个用电场所向汇点连一条容量是cc的弧
        {
            while(getchar()!='(');
            scanf("%d)%d",&u,&cc);
            c[u+1][t]=cc;
        }
        pro();  //求最大流
    }
    return 0;
}

转载于:https://www.cnblogs.com/MisdomTianYa/p/6581859.html