正睿OI游记
转载请注明来源!
Day0x01
上午打了一场模拟赛。
T1
:给定\(x\),求是否有正整数\(a,b,c\)满足\(a\times b=c \ \&\& \ a+b+c=x\)
做法
\[ \begin{align} a+b+c&=x \\ \text{即}a+b+ab&=x \\ \text{即}a+b+ab+1&=x+1 \\ \text{即}(a+1)(b+1)&=x+1 \end{align} \]
判断\((x+1)\)是否质数即可.
T2
在\(N\times M\)的格子中,每个格子有一个颜色。
一变色龙位于\((x,y)\),每经过一个格子,变色龙就会使自己的颜色和格子颜色一致
求变色龙到每个格子的颜色最少变化次数。
做法:
显然的01_bfs
或dfs加剪枝也能过。
code:
#include<bits/stdc++.h>
using namespace std;
const int inf=0x3f3f3f3f, maxn=100007, mod=1e9+7;
const ll linf=0x3f3f3f3f3f3f3f3fLL;
const ll P=19260817;
deque<pii> q;
int n,m,sx,sy;
int a[2007][2007];
int dis[2007][2007];
int vis[2007][2007];
const int dx[]={0,1,0,-1},dy[]={1,0,-1,0};
bool Good(int x,int y){
if(x>=1&&x<=n&&y>=1&&y<=m)return true;
return false;
}
int main(){
scanf("%d%d%d%d",&n,&m,&sx,&sy);
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
scanf("%d",&a[i][j]);
dis[i][j]=inf;
}
}
dis[sx][sy]=0;
q.pb(mp(sx,sy));
while(!q.empty()){
int x=q.front().first,y=q.front().second;
q.pop_front();
if(vis[x][y])continue;
vis[x][y]=true;
for(int d=0;d<4;d++){
int nx=x+dx[d],ny=y+dy[d];
if(Good(nx,ny)&&a[nx][ny]==a[x][y]){
dis[nx][ny]=min(dis[nx][ny],dis[x][y]);
q.push_front(mp(nx,ny));
}
}
for(int d=0;d<4;d++){
int nx=x+dx[d],ny=y+dy[d];
if(Good(nx,ny)&&a[nx][ny]!=a[x][y]){
dis[nx][ny]=min(dis[nx][ny],dis[x][y]+1);
q.push_back(mp(nx,ny));
}
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
printf("%d ",dis[i][j]);
}
printf("\n");
}
return 0;
}
T3
在一个串\(s\)中只包含(,),*,且*恰出现一次。
求包含*(且*在某个括号内)的合法括号序列个数。
\(\vert s\vert<=10^6 \)
做法:
用栈来维护括号序列。
左括号则进栈,右括号则出栈。
判断有多少个匹配满足包含*
代码
#include<bits/stdc++.h>
using namespace std;
const int inf=0x3f3f3f3f, maxn=200007, mod=1e9+7;
char s[maxn];
stack <int >st;
int main(){
scanf("%s",s);
int n=strlen(s);
int pos=0;//position of "*"
for(int i=0;i<n;i++)if(s[i]=='*')pos=i;
int rt=0;
int ans=0;
for(int i=0;i<n;i++){
if(s[i]=='('){
st.push(i);
}
if(s[i]==')'){
if(st.empty()){// if invalid
ans=max(ans,rt);
rt=0;
continue;
}
int j=st.top();
st.pop();
if(j<pos&&i>pos)rt++;
}
}
printf("%d",max(rt,ans));
return 0;
}
T4
求序列\(a\)的最长回文子序列。
其中$|a| \leq 5 \times 10^4,a_i\leq 10^5, $
另外每个数出现次数\(k\leq 4\)
做法:
首先有结论:一个序列的最长回文子序列 等于原序列和反序列(即\(b_i=a_{n-i+1}\))的最长公共子序列。
因此得到40pts.做法:\(O(n^2)\)求最长公共子序列。
100pts:
注意到数据范围中存在\(k\leq 4\)的限制。
在求\(a,b\)最长公共子序列中只有\(a_i==b_j\)才有转移的必要。
因此DP中只有\(4*4*10^5 \le 2*10^6\)个决策点。
计每一个\(a_i==b_j\)的决策点为\((i,j)\),可以表示成坐标轴内的一个点。
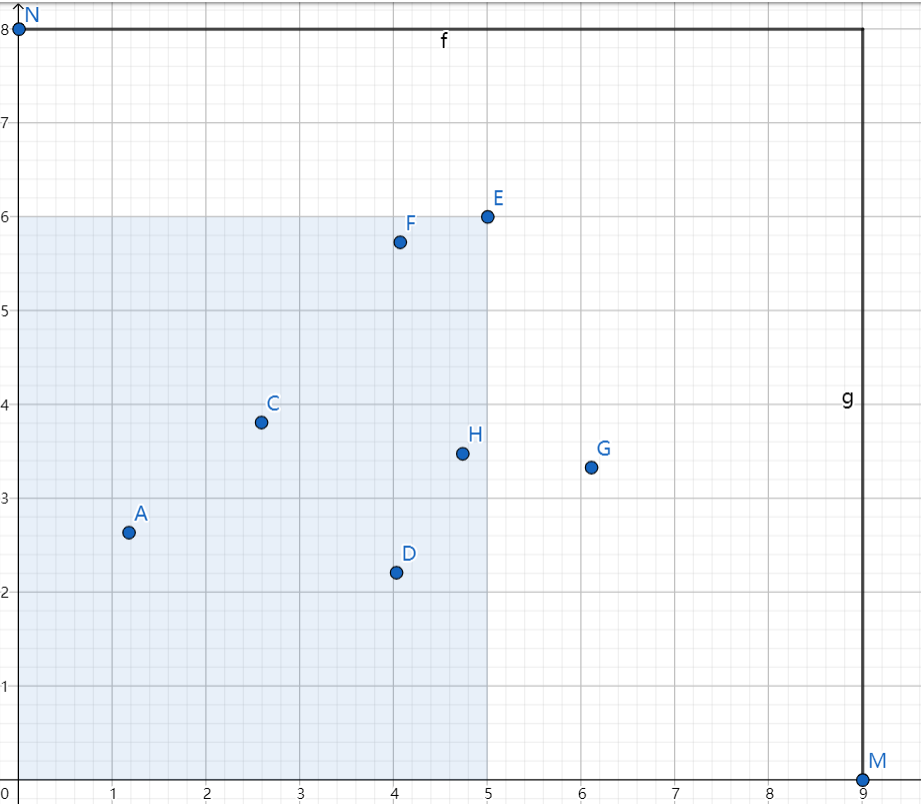
考虑决策点的转移,例如点\(E\)显然可以从以下的矩形区域中转移。
得到转移方程
\[ dp[i]=\operatorname{max}\limits_{j \in Matrix \ i}dp[j]+1 \]
转移顺序是自左而右,自上而下
所以矩形右上端点的dp值一定大于以内的端点值。
更进一步若点\(\forall P(i_1,j),Q(i_2,j)(i_1>i_2) \rightarrow dp[P]\ge dp[Q]\)
所以可以用线段树维护在横线\(y=i\)的最大值。
具体而言,对于点\((i,j)\)查询时查\([1,i-1]\)的最大值,修改\(i\)上的值。
代码:
#include<bits/stdc++.h>
using namespace std;
typedef vector<int > vi;
typedef pair<int ,int > pii;
typedef vector<pii> vii;
const int inf=0x3f3f3f3f, maxn=50007, mod=1e9+7;
const ll linf=0x3f3f3f3f3f3f3f3fLL;
const ll P=19260817;
int T;
vi v[maxn<<1];
int n,k;
int a[maxn];
pii b[maxn<<2];
int m;
struct SGT{
int t[maxn<<2];
void pushup(int id){
t[id]=max(t[id<<1],t[id<<1|1]);
}
void build(int id,int l,int r){
if(l==r){
t[id]=0;
return ;
}
int mid=l+r>>1;
build(id<<1,l,mid);
build(id<<1|1,mid+1,r);
pushup(id);
}
void update(int id,int l,int r,int pos,int val){
if(l==r){
t[id]=val;
return ;
}
int mid=l+r>>1;
if(pos<=mid)update(id<<1,l,mid,pos,val);
else update(id<<1|1,mid+1,r,pos,val);
pushup(id);
}
int query(int id,int l,int r,int L,int R){
if(L<=l&&r<=R){
return t[id];
}
if(L>R)return 0;
int mid=(l+r)>>1;
int ans=0;
if(L<=mid)ans=max(ans,query(id<<1,l,mid,L,R));
if(R>mid) ans=max(ans,query(id<<1|1,mid+1,r,L,R));
return ans;
}
}Tree;
bool cmp(const pii& a,const pii &b ){
if(a.first==b.first)return a.second>b.second;
return a.first<b.first;
}
int main(){
scanf("%d",&T);
while(T--){
scanf("%d%d",&n,&k);
int mx=0;
for(int i=1;i<=100000;i++){v[i].clear();
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
mx=max(a[i],mx);
v[a[i]].pb(i);
}
m=0;
for(int i=1;i<=mx;i++)
for(int j=0;j<v[i].size();j++)
for(int k=0;k<v[i].size();k++)
b[++m]=mp(v[i][j],n-v[i][k]+1);
sort(b+1,b+1+m,cmp);
Tree.build(1,1,50000);
for(int i=1;i<=m;i++){
int x=b[i].first,y=b[i].second;
int rt=Tree.query(1,1,50000,1,y-1);
Tree.update(1,1,50000,y,rt+1);
}
printf("%d\n",Tree.t[1]);
}
return 0;
}
T5
在平面直角坐标系中有\(n\)条形如\(x+y=c\),\(m\)条形如\(x-y=c\)的直线
求在\((0,0)到(w,h)\)的矩形范围内这些直线形成了多少矩形。
做法
首先我们考虑将坐标轴旋转45度,那么现在只有横的和竖的线段。
对于一个矩形,我们要找的两条横着的线段两条竖着的线段。假设两条横着的线段在矩阵中的\(x\)坐标范围是\([l_1, r_1]\),\([l_2, r_2]\),竖着的线段的横坐标是\(x_1, x_2\),那么构成矩形的条件就是\(max(l_1, l_2) \leq x_1, x_2\leq \min(r_1, r_2)\)。
一个小问题是如何求出旋转\(45\)度之后的横纵坐标,实际上我们只需要将\((x,y)\)变化成\((x+y, x-y)\)即可,对于\(x\)坐标的范围,只需要简单地解不等式即可。
所以\(O(n^3)\)的做法就是枚举两条竖的线段,然后\(O(n)\)求出所有两个端点在\(x_1, x_2\)两边的横线段,计算即可。
后面的\(O(n)\)枚举可以改成预处理加前缀和,所以可以在\(O(1)\)时间复杂度内计算出来,这样就可以在\(O(n^2)\)时间内完成。
\(O(n \log n)\)的做法比较复杂。首先我们将所有竖的线段按照\(x\)坐标离散化,我们考虑从左到右枚举左边的一条竖的线段,然后使用线段树统计右边一条竖的线段的答案。假设左边的竖线段是\(x_l\),那么对于一条跨过\(x_l\)的横线段,即\(l_1\leq x_l\leq r_1\),那么会对\([x_l, r_1]\)之间的所有竖线段有贡献。所以我们使用扫描线处理左端点的时候,贡献的变化可以看成区间加减\(1\)。我们需要支持区间加减\(1\),然后求区间中的数字\(\binom{x}{2}\)的和的操作,这些都可以使用线段树解决。
代码:
#include<bits/stdc++.h>
#define mp make_pair
#define pb push_back
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef vector<int > vi;
typedef pair<ll ,ll > pii;
typedef vector<pii> vii;
const int inf=0x3f3f3f3f, maxn=100007;
const ll mod=1e9+7;
const ll linf=0x3f3f3f3f3f3f3f3fLL;
const ll P=19260817;
ll w,h,n,m;
ll c[maxn];
vii evt;
struct SGT{
struct node{
ll lazy,s1,s2;
int s0;
}t[maxn<<2];
void pushup(int id){
t[id].s1=t[id<<1].s1+t[id<<1|1].s1;
t[id].s2=t[id<<1].s2+t[id<<1|1].s2;
}
void change(int id,int val){
t[id].lazy+=val;
t[id].s2+=(val-1)*val/2*t[id].s0+val*t[id].s1;
t[id].s1+=val*t[id].s0;
}
void pushdown(int id){
if(t[id].lazy){
change(id<<1,t[id].lazy);
change(id<<1|1,t[id].lazy);
t[id].lazy=0;
}
}
void build(int id,int l,int r){
t[id].lazy=t[id].s1=t[id].s2=0;
t[id].s0=r-l+1;
if(l==r)return ;
int mid=l+r>>1;
build(id<<1,l,mid);
build(id<<1|1,mid+1,r);
pushup(id);
}
void update(int id,int l,int r,int L,int R,int val){
if(L<=l&&r<=R){
change(id,val);
return ;
}
pushdown(id);
int mid=(l+r)>>1;
if(L<=mid)update(id<<1,l,mid,L,R,val);
if(R>mid)update(id<<1|1,mid+1,r,L,R,val);
pushup(id);
}
ll query(int id,int l,int r,int L,int R){
if(L<=l&&r<=R){
return t[id].s2;
}
pushdown(id);
int mid=(l+r)>>1;
ll ans=0;
if(L<=mid)ans+=query(id<<1,l,mid,L,R);
if(R>mid)ans+=query(id<<1|1,mid+1,r,L,R);
return ans;
}
}T;
int main(){
scanf("%lld%lld%lld%lld",&w,&h,&n,&m);
for(int i=1;i<=n;i++){
scanf("%lld",c+i);
evt.pb(mp(c[i],inf));
}
sort(c+1,c+n+1);
for(int i=1;i<=m;i++){
ll d;
scanf("%lld",&d);
ll p1=min(w+h,min(2*w-d,2*h+d));
ll p2=max(0ll,max(-d,d));
evt.pb(mp(p2,p1));
}
sort(evt.begin(),evt.end());
T.build(1,1,n);
ll ans=0;
for(int i=0;i<(int ) evt.size();i++){
ll x=evt[i].first,y=evt[i].second;
if(y==inf){
int id=lower_bound(c+1,c+1+n,x)-c;
if(id<n)ans=(ans+T.query(1,1,n,id,n)%mod)%mod;
}else{
int id=upper_bound(c+1,c+n+1,y)-c-2;
if (id>=1) T.update(1,1,n,1,id,1);
}
}
printf("%lld",ans%mod);
return 0;
}
T6
水题。
判一下有多少个重复数即可。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef vector<int > vi;
typedef pair<int ,int > pii;
typedef vector<pii> vii;
const int inf=0x3f3f3f3f, maxn=100007, mod=1e9+7;
const ll linf=0x3f3f3f3f3f3f3f3fLL;
const ll P=19260817;
int biao[6][3]={
{0,0,5},
{0,0,5},
{0,5,10},
{5,10,200},
{10,200,3000},
{3000,250000,5000000}
};
int ans1,ans2;
set<int > a,b;
int main(){
for(int i=1;i<=5;i++){
int rt;
scanf("%d",&rt);
a.insert(rt);
}
for(int i=1;i<=2;i++){
int rt;
scanf("%d",&rt);
b.insert(rt);
}
for(int i=1;i<=5;i++){
int rt;
scanf("%d",&rt);
if(a.find(rt)!=a.end())ans1++;
}
for(int i=1;i<=2;i++){
int rt;
scanf("%d",&rt);
if(b.find(rt)!=b.end())ans2++;
}
printf("%d",biao[ans1][ans2]);
return 0;
}





















 95
95











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








