题目描述
树可以用来表示物种之间的进化关系。一棵“进化树”是一个带边权的树,其叶节点表示一个物种,两个叶节点之间的距离表示两个物种的差异。现在,一个重要的问题是,根据物种之间的距离,重构相应的“进化树”。
令N={1..n},用一个N上的矩阵M来定义树T。其中,矩阵M满足:对于任意的i,j,k,有M[i,j] + M[j,k] >= M[i,k]。树T满足:
1.叶节点属于集合N;
2.边权均为非负整数;
3.dT(i,j)=M[i,j],其中dT(i,j)表示树上i到j的最短路径长度。
如下图,矩阵M描述了一棵树。
树的重量是指树上所有边权之和。对于任意给出的合法矩阵M,它所能表示树的重量是惟一确定的,不可能找到两棵不同重量的树,它们都符合矩阵M。你的任务就是,根据给出的矩阵M,计算M所表示树的重量。下图是上面给出的矩阵M所能表示的一棵树,这棵树的总重量为15。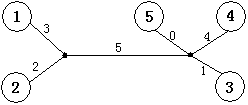
输入格式
输入数据包含若干组数据。每组数据的第一行是一个整数n(2<n<30)。其后n-1行,给出的是矩阵M的一个上三角(不包含对角线),矩阵中所有元素是不超过100的非负整数。输入数据保证合法。
输入数据以n=0结尾。
输出格式
对于每组输入,输出一行,一个整数,表示树的重量。
输入1
5
5 9 12 8
8 11 7
5 1
4
4
15 36 60
31 55
36
0
输出1
15
71
挺有意思的一个思考题,直接搬运洛谷的题解吧,感觉讲得很好:
锻炼思维的好题,需要运用一些树的性质。以下用g(i,j)表示点i与点j之间的距离。
首先,我们考虑n=2时的情况,很显然答案就是g(1,2)。
接下来考虑n=3时的情况。由于所有点均为叶子节点,很显然点3是从点1到点2的路径上分叉出来的,就像下图。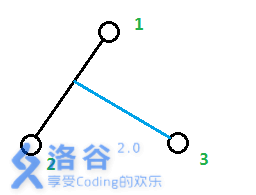
设蓝色部分长度为len,那么答案就是g(1,2)+len。len怎么求呢?显然,len = (g(1,3)+g(2,3)-g(1,2))/2。
n>3的情况也同理。枚举i,看看点n是不是从点1~i的路径上分叉出来的,求出的最小len就是要加到答案里面去的。如下图。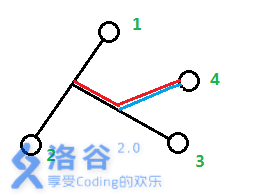
如果认为点4是从1~2的路径上分叉出来的,答案就会加上红色部分的长度。但是红色部分长度显然有一部分是多余的。只有认为点4是从1~3的路径上分叉出来的,才能加上正确答案(也就是蓝色部分)。
附上根据该思路写出来的代码,这个题解已经讲的很好了,估计各位神犇不需要看也能写出来(主要是代码写的太丑了)
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<queue>
#include<vector>
#include<algorithm>
#define inf 0x3f3f3f3f
#define maxn 55
#define maxm 10005
#define _for(i,a,b) for(int i=(a);i<(b);++i)
#define _rof(i,a,b) for(int i=(a);i>(b);--i)
#define _rep(i,a,b) for(int i=(a);i<=(b);++i)
#define _per(i,a,b) for(int i=(a);i>=(b);--i)
using namespace std;
typedef long long ll;
int a[maxn][maxn];
int n;
int main(){
int ans,tmp;
while(scanf("%d",&n)==1 && n){
_rep(i,1,n)_rep(j,i+1,n)scanf("%d",&a[i][j]);
ans=a[1][2];
_rep(j,3,n){
tmp=(a[1][j]+a[2][j]-a[1][2])/2;
_rep(i,2,j-2)
tmp=min(tmp, (a[i][j]+a[i+1][j]-a[i][i+1])/2);
ans+=tmp;
}
printf("%d\n",ans);
}
return 0;
}




















 211
211











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








