【数据结构与算法】（一）时间复杂度分析、空间复杂度分析、最好复杂度、最坏复杂度、平均复杂度、均摊时间复杂度

 

目录

 

复杂度分析的意义

时间复杂度分析

 1.简单情况

2.由多种复杂度的程序段组成，则整体上取决于复杂度最高的一部分（加法法则）  O(n^2 + n + 1)这种，近似为 O（n^2）

3. 受多个变量影响时，不能忽略任何一个变量

空间复杂度

常见的复杂度

最好复杂度、最坏复杂度

平均情况时间复杂度

均摊时间复杂度

---

复杂度分析的意义

数据结构与算法：

     数据结构：是数据的组织、管理和存储格式，使用目的是为了更高效的访问和修改数据。

数据结构的组成方式有：线性结构：包括数组、链表以及由他们衍生出来的栈、队列、哈希表。树、图等及其他由这些基础数据结构变化而来的其他数据结构等。

     算法：操作数据

衡量算法操作数据的效率可以通过实际的运行来得到一次大致的结果，但是每次运行，受运行的物理设备环境、运行时的性能、测试数据规模、测试数据规律等影响。通过时间复杂度、空间复杂度，可以暂时排除其他因素影响，得到程序执行效率和资源消耗与数据规模 n之间的关系。实际运行起还是要受这些外部因素影响的，所以时间复杂度高的也并不一定比时间复杂度低的运行慢。

为啥要分析算法的复杂度呢？掌握数据结构与算法，及复杂度分析有助于提高代码的效率及理解其他框架的设计思想。嗯。

时间复杂度的全称是渐进时间复杂度，表示算法的执行时间与数据规模之间的增长关系。类比一下，空间复杂度全称就是渐进空间复杂度（asymptotic space complexity），表示算法的存储空间与数据规模之间的增长关系。 

时间复杂度分析

从 CPU 的角度来看，这段代码的每一行都执行着类似的操作：读数据-运算-写数据。尽管每行代码对应的 CPU 执行的个数、执行的时间都不一样，但是，我们这里只是粗略估计，所以可以假设每行代码执行的时间都一样：

 1.简单情况

 int cal(int n) {
   int sum = 0;
   int i = 1;
   int j = 1;
   for (; i <= n; ++i) {
     j = 1;
     for (; j <= n; ++j) {
       sum = sum +  i * j;
     }
   }
 }

•  对于不涉及n 的，如 int sum , i, j 声明的三行，与n的大小无关，这部分为 O(1)
•  对于   for (; i <= n; ++i)  ， j= 1 这部分，将被循环 执行 n次， 共计 2n 次，与n是线性关系，这种与n是线性关系的，无论多少倍的关系，时间复杂度都为 O(n)
•  对于   for (; j <= n; ++j) 这个嵌套进去的循环的两行代码，外层的每次循环，这个嵌套循环都将被循环 n次，所以这两行代码共计循环 2n^2次，和 n 是2次方关系，时间复杂度为 O（n^2)

2.由多种复杂度的程序段组成，则整体上取决于复杂度最高的一部分（加法法则）  O(n^2 + n + 1)这种，近似为 O（n^2）

int cal(int n) {
   int sum_1 = 0;
   int p = 1;
   for (; p < 100; ++p) {
     sum_1 = sum_1 + p;
   }

   int sum_2 = 0;
   int q = 1;
   for (; q < n; ++q) {
     sum_2 = sum_2 + q;
   }
 
   int sum_3 = 0;
   int i = 1;
   int j = 1;
   for (; i <= n; ++i) {
     j = 1; 
     for (; j <= n; ++j) {
       sum_3 = sum_3 +  i * j;
     }
   }
 
   return sum_1 + sum_2 + sum_3;
 }

•  对于上面这种，受一个 n的规模影响，但是有多段不同复杂度的程序组成的算法，时间复杂度取决于复杂度最高的一部分程序

3. 受多个变量影响时，不能忽略任何一个变量

int cal(int m, int n) {
  int sum_1 = 0;
  int i = 1;
  for (; i < m; ++i) {
    sum_1 = sum_1 + i;
  }

  int sum_2 = 0;
  int j = 1;
  for (; j < n; ++j) {
    sum_2 = sum_2 + j;
  }

  return sum_1 + sum_2;
}

• 对于以上受多个变量并列影响，时间复杂度则不是单纯的受某一个影响，可以理解为两部分都分别耗时，时间复杂度应该为 O（m + n）

int cal(int n, int m) {
   int ret = 0; 
   int i = 1;
   for (; i < n; ++i) {
     ret = ret + f(m);
   } 
 } 
 
 int f(int n) {
  int sum = 0;
  int i = 1;
  for (; i < n; ++i) {
    sum = sum + i;
  } 
  return sum;
 }

• 对于以上受多个变量嵌套影响： n次循环中嵌套了f(m)是一个m次循环，则复杂度为 O(m * n)

空间复杂度

和时间复杂度计算类似，就是看程序占用的内存空间的大小和n的规模之间的关系。

当算法的存储空间大小固定，和输入规模 n 没有直接的关系时，空间复杂度记作 O(1)

void fun1(int n){
    int var = 3; 
    return var;
}

当算法分配的空间是一个线性的集合（如数组），并且集合大小和输入 规模n成正比时，空间复杂度记作O(n) 。

当算法分配的空间是一个二维数组集合，并且集合的长度和宽度都与输 入规模 n 成正比时，空间复杂度记作 O(n^2 ) 。

 

void fun(int n){
    int[][] matrix = new int[n][n];
    ......
}

 递归空间

递归是一个比较特殊的场景。虽然递归代码中并没有显式地声明变量或 集合，但是计算机在执行程序时，会专门分配一块内存，用来存储 “方 法调用栈 ”。 “方法调用栈”包括进栈 和出栈 两个行为。 当进入一个新方法时，执行入栈操作，把调用的方法和参数信息压入栈 中。当方法返回时，执行出栈操作，把调用的方法和参数信息从栈中弹出。

1. void fun4(int n){
2.     if(n<=1){
3.         return; 
4.     } 
5.     fun4(n-1); 
6.     …
7. }

执行递归操作所需要的内存空间和递归的深度成正比。纯粹的递归操作的空间复杂度也是线性的，如果递归的深度是 n ，那么空间复杂度就是 O(n) 。

 

常见的复杂度

实际运行起还是要受外部因素影响的！！！

最好复杂度、最坏复杂度

// n表示数组array的长度
int find(int[] array, int n, int x) {
  int i = 0;
  int pos = -1;
  for (; i < n; ++i) {
    if (array[i] == x) pos = i;
  }
  return pos;
}

根据前面的分析，此 find()函数找到 array数组中值为 x的下标 的时间复杂度为 O(n)，由n决定

// n表示数组array的长度
int find(int[] array, int n, int x) {
  int i = 0;
  int pos = -1;
  for (; i < n; ++i) {
    if (array[i] == x) {
       pos = i;
       break;
    }
  }
  return pos;
}

但是，加了break后， find函数的时间复杂度有了不确定性，找到下标位置后就结束了； 这时候存在两种极端情况：

第一种，下标为0的位置就是 x 存在的位置，只执行一次，复杂度为O（1）

第二种， x压根不存在于array数组种，for循环完成了n次循环也没有break，最后反悔了pos=-1，复杂度为O（n）

第一种就是最好复杂度， 即 ，在最理想的情况下，执行这段代码的时间复杂度

第二种就是最坏复杂度，即，在最糟糕的情况下，执行这段代码的时间复杂度

平均情况时间复杂度

最好情况时间复杂度和最坏情况时间复杂度对应的都是极端情况下的代码复杂度，发生的概率其实并不大。为了更好地表示平均情况下的复杂度，引入：平均情况时间复杂度，简称为平均时间复杂度。

// n表示数组array的长度
int find(int[] array, int n, int x) {
  int i = 0;
  int pos = -1;
  for (; i < n; ++i) {
    if (array[i] == x) {
       pos = i;
       break;
    }
  }
  return pos;
}

还是加了break的find函数：

在这个find函数中，x的位置要么在数组中，要么不在。在和不在的概率都是 1/2, 如果在数组中，则在数据n个位置中 ，每个位置的概率都是 1/n, 总体上是 1/2n, 那么循环1次找到x的时间为1，循环2次时间为2.....循环n次的时间为 n，加上x不存在在array中的情况，复杂度的加权平均值为

 

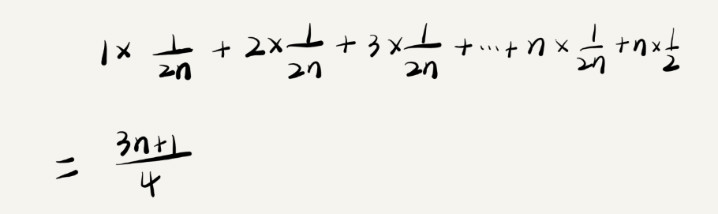
这里所有的概率和为1，计算时省略了分母；

简单的概况，就是 每种不确定情况的时间花费 *  概率 求和 

结论：加了Break函数这段代码的加权平均时间复杂度仍然是 O(n)；

均摊时间复杂度

对一个数据结构进行一组连续操作中，大部分情况下时间复杂度都很低，只有个别情况下时间复杂度比较高，而且这些操作之间存在前后连贯的时序关系，这个时候，我们就可以将这一组操作放在一块儿分析，看是否能将较高时间复杂度那次操作的耗时，平摊到其他那些时间复杂度比较低的操作上。而且，在能够应用均摊时间复杂度分析的场合，一般均摊时间复杂度就等于最好情况时间复杂度。

学习笔记，欢迎指正~