数据结构（五）——二分搜索树

最新推荐文章于 2022-12-05 00:51:29 发布
最新推荐文章于 2022-12-05 00:51:29 发布
阅读量330 收藏 1
点赞数
文章标签： 二分搜索树
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/baoyu_g/article/details/81033037
版权

    简单的说，二分搜索树是一种某个节点的左孩子小于这个节点的值，右孩子大于这个节点的值的特殊二叉树。（什么是二叉树就不说了），特点是：二分搜索树的中序遍历得到的结果是有序的；这篇博客的大致目录：

1.二分搜索树添加节点

2.判断是否存在某个数据

2.递归的先序、中序和后序遍历

3.借助栈的先序非递归遍历

4.层序遍历(广度优先遍历)

5.查找最大值和最小值

6.删除最大值和最小值

7.删除任意元素

8.时间复杂度分析

  • 首先是二分搜索树的创建，向二分搜索树中添加节点的实现:

思路：如果树为空的话，创建一个Node存储要添加的数据并将这个节点作为树的根；

          如果树不为空，如果添加的值大于当前节点的值，则往当前节点的右子树添加；

                                 如果添加的值小于当前节点的值，则往当前节点的左子树添加；

                                 如果添加的值等于当前节点的值，忽略即可，不再添加到树中；

首先准备一个节点Node：使用泛型表示节点中可以存放任意类型的数据,并且要求E继承Comparable，是可比较大小的；每个节点应保存其左孩子和右孩子的信息。

public class Node<E extends Comparable<E>>{
		private E e;
		private Node left;
		private Node right;
		
		public Node(E e) {
			this.e = e;
			this.left = null;
			this.right = null;
		}
		
}

一个二分搜索树应当具备的属性：根节点root和树的大小size：

package com.gby.tree;

import java.util.Stack;

public class BST<E extends Comparable<E>> {
	
	public class Node<E extends Comparable<E>>{
		private E e;
		private Node left;
		private Node right;
		
		public Node(E e) {
			this.e = e;
			this.left = null;
			this.right = null;
		}
		
	}
	
	//一个树应当具备根节点和size两个属性
	private Node root;
	private int size;
	
	public BST(Node root) {
		this.root = root;
		this.size = 0;
	}
	//初始化时root为Null, size为0
	public BST() {
		this.root = null;
		this.size = 0;
	}
	
	public int getSize(){
		return size;
	}
	
}

添加节点：    

        public void add(E e){
		root = add(root,e);
	}

	//参数node为要添加元素e的树的根，返回添加节点的后，树新的的根
	private Node add(Node node, E e) {
		
		//如果添加元素的树的根为null，即树为空,直接创建一个新的节点作为根
		if(node == null){
			size ++;
			return new Node(e);
		}  		
		
		//树不为空
		if(e.compareTo((E) node.e) < 0){    		//添加的元素小于根节点的元素值，则加入左子树；左孩子为空则创建
			node.left = add(node.left,e);
		}else if(e.compareTo((E) node.e) > 0){   	//添加的元素大于根节点的元素值，则加入右子树；右孩子为空则创建
			node.right = add(node.right,e);
		}
		
		size++;
		return node;
	}

  • 判断是否存在某个节点：
        //查询元素，返回节点所在树的根
	public boolean contains(E e){
		return contains(root, e);
	}
	
	public boolean contains(Node node,E e){
		if(node == null){
			return false;
		}
		
		if(e.compareTo((E) node.e) < 0){
			return contains(node.left,e);
		}else if(e.compareTo((E) node.e) == 0){
			return true;
		}else 
			return contains(node.right,e);
	}

  • 先序遍历：    先访问根节点，再先序遍历左子树，再先序遍历右子树
        //先序遍历二分搜索树
	public void preOrder(){
		preOrder(root);
	}

	//先序遍历以node为根的二分搜索树
	private void preOrder(Node node) {
		if(node == null)
			return;
		System.out.println(node.e);    //以输出表示访问
		preOrder(node.left);
		preOrder(node.right);
	}

中序遍历和后序遍历：    

        //中序遍历
	public void inOrder(){
		inOrder(root);
	}

	private void inOrder(Node node) {
		if(node == null){
			return;
		}
		inOrder(node.left);
		System.out.println(node.e);
		inOrder(node.right);
		
	}
	//后序遍历
	public void postOrder(){
		postOrder(root);
	}
	
	private void postOrder(Node node){
		if(node == null){
			return;
		}
		postOrder(node.left);
		postOrder(node.right);
		System.out.println(node.e);
	}

借助于栈的非递归先序遍历：    

        /**
	 * 二分搜索树的非递归遍历
	 */
	public void preOrderNR(){
		Stack<Node> stack = new Stack<Node>();
		stack.push(root);
		while(!stack.isEmpty()){
			Node cur = stack.pop();
			System.out.println(cur.e);  //访问根节点
			
			//依次将cur的右孩子和左孩子入栈，因为栈具有后入先出的特点，先序遍历需要先遍历左子树，所以左孩子先出栈，则后入栈
			if(cur.right!=null)
				stack.push(cur.right);
			if(cur.left!=null)
				stack.push(cur.left);
		}
	}

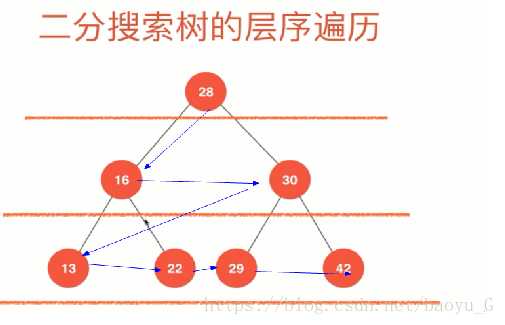
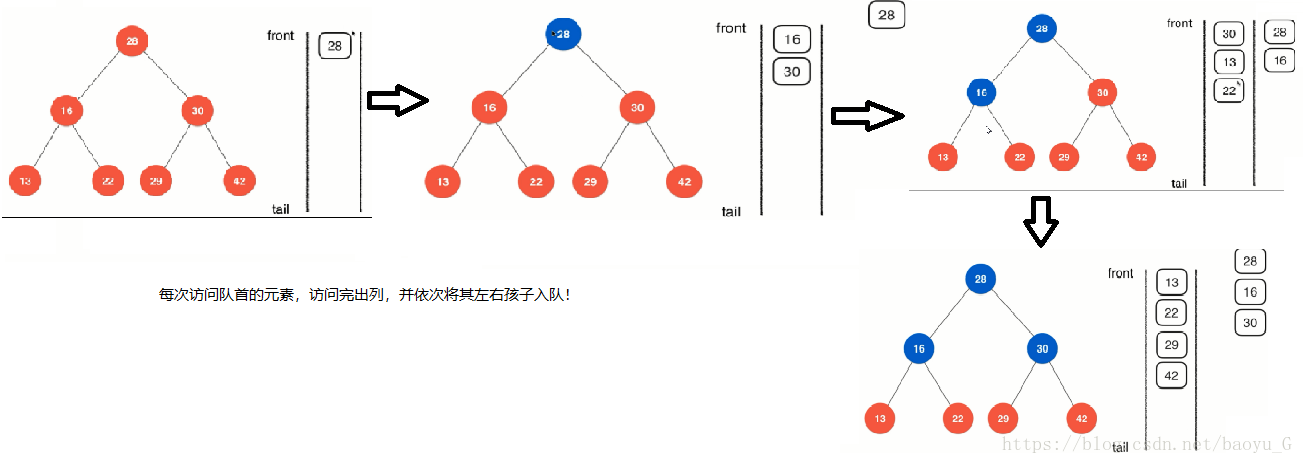
  • 层序遍历：先序、中序和后序遍历本质上都是深度优先遍历，层序遍历是一种广度优先的遍历，遍历的方式为：

28-16-30-13-22-19-42

借助于队列实现层序遍历：


public void levelOrder(){
		Queue<Node> queue = new LinkedList<Node>();
		queue.add(root);
		while(!queue.isEmpty()){
			Node node = queue.remove();
			System.out.println(node.e);
			if(node.left!=null)
				queue.add(node.left);
			if(node.right!=null)
				queue.add(node.right);
		}
		
}  

  • 查找最大值和最小值

    前面说，平衡二叉树具有某个节点的左孩子小于这个节点，右孩子大于这个节点的特点；所以，某个节点的左孩子一定小于这个节点，右孩子一定大于这个节点。那么，对于一个平衡二叉树，最小的节点就是从根节点开始，不断向左子树遍历，直到找到一个没有左孩子的节点，最大的节点就是不断向右子树遍历，直到找到一个没有右孩子的节点；这就是查找最大值和最小值的思路。

    下面是代码实现：

	//二分搜索树中最大的元素
	public E maxNum(){
		if(size == 0)
			throw new IllegalArgumentException("no node in bst.");
		return (E) maxNum(root).e;
	}
	//在参数node为根的树中查找最大值，并返回最大值所在的节点
	private Node maxNum(Node node){
		if(node.right == null)
			return node;
		return maxNum(node.right);
	}
首先是查找最大的元素：用户默认调用maxNum（）方法，先判断树是否为空，如果为空，抛出异常；不为空则调用私有的maxNum(Node node)方法，在以root为根的树中查找最大值；如果根本身没有右孩子，那么这个根就是以它所在这个树中的最大节点；node有右孩子时，就以node.right为根查找node右子树的最大值，如此递归；

相似的，下面是最小值的查找：

	//寻找二分搜索树中最小的元素
	public E miniNum(){
		if(size == 0)
			throw new IllegalArgumentException("no node in bst.");
		return 	(E) miniNum(root).e;
	}

	public Node miniNum(Node node){
		if(node.left == null){
			return node;
		}
		return miniNum(node.left);
	}
  • 删除最大值和最小值

据上，最大节点是没有右孩子的，最小节点是没有左孩子的；但是，最大节点可以有左孩子，最小的节点可以有右孩子；所以需要保留最大节点的左子树和最小节点的右子树，将最大节点的左子树的根替代最大节点的位置，最小节点的右子树的根替代最小节点的位置；

	//删除最大的元素
	public E removeMax(){
		E max = maxNum();
		removeMax(root);
		return max;
	}
	
	//删除以node为根的树的最大节点(node.right=null)，并返回新的根
	private Node removeMax(Node node) {
		if(node.right==null){			//根节点的右孩子为空，则根为这个树的最大节点
			Node leftChild = node.left;
			node.left = null;
			size--;                        //维护size的大小
			return leftChild;
		}
		node.right = removeMax(node.right);    //根有右孩子，不是最大节点
		return node;
	}

删除最大节点时，如果根就是最大节点，则新的根就是左孩子；如果根不是最大节点，即根有右孩子，则在右子树中找最大值并删除；如果根的右孩子就是最大值，而右孩子又有左孩子，删除右孩子需要让根的右孩子变为根的右孩子的左孩子，所以需要将左孩子（要删除的节点的子树的根）返回，赋值给node.right，把这棵树连起来；所以有了上面的代码。

    类似的，下面时删除最小的节点：    

        //删除二分搜索树中最小的元素
	public E removeMiniNum(){
		E e = miniNum();
		removeMiniNum(root);
		return e;
	}
	
	private Node removeMiniNum(Node node) {
		if(node.left==null){
			Node rightNode = node.right;
			node.right=null;
			size--;
			return rightNode;
		}
		node.left = removeMiniNum(node.left);
		return node;
	}
  • 删除二分搜索树中的任意一个节点    
	//删除以node为根的树中的e，并返回新的树的根节点
	private Node remove(Node node,E e){
		if(node==null)                            //根为Null,直接返回
			return node;
		
		if(e.compareTo((E) node.e)<0){            //如果e小于当前节点，则进入左子树寻找
			node.left = remove(node.left,e);
		}else if(e.compareTo((E) node.e)>0){      //e大于当前节点，进入右子树寻找，并返回右子树删除后的根节点和前面的节点保持连接
			node.right=remove(node.right,e); 
		}else{								 //node.e = e
			if(node.left==null){                //要删除的节点没有左子树，则把右子树的根节点返回给上一层循环的node.X连接起来
				Node rightNode = node.right;
				node.right = null;
				size--;
				return rightNode;
			}else if(node.right==null){
				Node leftNode = node.left;
				node.left = null;
				size--;
				return leftNode;
			}
			//待删除的节点的左右子树均不为空，则找到右子树的最小值或者左子树的最大值替代这个节点
			Node successor = miniNum(node.right);
			successor.right = removeMiniNum(node.right);
			successor.left =  node.left;
			node.left = node.right = null;
			return successor; 
		}
		return null;
	}
以上就是二分搜索树的常用操作，这里的二分搜索树在添加元素时，对于已经存在的元素不做处理，即没有重复元素；如果需要保存重复元素，可自行定义插入方式。

  完整代码：

package com.gby.tree;

import java.util.LinkedList;
import java.util.Queue;
import java.util.Stack;

import com.gby.tree.BST.Node;

public class BST<E extends Comparable<E>> {
	
	public class Node<E extends Comparable<E>>{
		private E e;
		private Node left;
		private Node right;
		
		public Node(E e) {
			this.e = e;
			this.left = null;
			this.right = null;
		}
		
	}
	
	//一个树应当具备根节点和size两个属性
	private Node root;
	private int size;
	
	public BST(Node root) {
		this.root = root;
		this.size = 0;
	}
	
	public BST() {
		this.root = null;
		this.size = 0;
	}
	
	public int getSize(){
		return size;
	}
	
	public void add(E e){
		root = add(root,e);
	}

	//返回添加节点的树的根
	private Node add(Node node, E e) {
		
		//如果添加元素的树的根为null，即树为空,直接创建一个新的节点作为根
		if(node == null){
			size ++;
			return new Node(e);
		}  		
		
		//树不为空
		if(e.compareTo((E) node.e) < 0){    		//添加的元素小于根节点的元素值，则加入左子树
			node.left = add(node.left,e);
		}else if(e.compareTo((E) node.e) > 0){   	//添加的元素大于根节点的元素值，则加入右子树
			node.right = add(node.right,e);
		}
		
		size++;
		return node;
	}
	
	//查询元素
	public boolean contains(E e){
		return contains(root, e);
	}
	
	public boolean contains(Node node,E e){
		if(node == null){
			return false;
		}
		
		if(e.compareTo((E) node.e) < 0){
			return contains(node.left,e);
		}else if(e.compareTo((E) node.e) == 0){
			return true;
		}else 
			return contains(node.right,e);
	}
	
	//先序遍历二分搜索树
	public void preOrder(){
		preOrder(root);
	}

	//先序遍历以node为根的二分搜索树
	private void preOrder(Node node) {
		if(node == null)
			return;
		System.out.println(node.e);
		preOrder(node.left);
		preOrder(node.right);
	}
	
	/**
	 * 二分搜索树的非递归遍历
	 */
	public void preOrderNR(){
		Stack<Node> stack = new Stack<Node>();
		stack.push(root);
		while(!stack.isEmpty()){
			Node cur = stack.pop();
			System.out.println(cur.e);  //访问根节点
			
			//依次将cur的右孩子和左孩子入栈，因为栈具有后入先出的特点，先序遍历需要先遍历左子树，所以左孩子先出栈，则后入栈
			if(cur.right!=null)
				stack.push(cur.right);
			if(cur.left!=null)
				stack.push(cur.left);
		}
	}
	
	//中序遍历
	public void inOrder(){
		inOrder(root);
	}

	private void inOrder(Node node) {
		if(node == null){
			return;
		}
		inOrder(node.left);
		System.out.println(node.e);
		inOrder(node.right);
		
	}
	//后续遍历
	public void postOrder(){
		postOrder(root);
	}
	
	private void postOrder(Node node){
		if(node == null){
			return;
		}
		postOrder(node.left);
		postOrder(node.right);
		System.out.println(node.e);
	}
	
	//基于队列的层序遍历
	public void levelOrder(){
		Queue<Node> queue = new LinkedList<Node>();
		queue.add(root);
		while(!queue.isEmpty()){
			Node node = queue.remove();
			System.out.println(node.e);
			if(node.left!=null)
				queue.add(node.left);
			if(node.right!=null)
				queue.add(node.right);
		}
		
	}
	
	//寻找二分搜索树中最小的元素
	public E miniNum(){
		if(size == 0)
			throw new IllegalArgumentException("no node in bst.");
		return 	(E) miniNum(root).e;
	}
	
	//二分搜索树中最小的元素；
	public Node miniNum(Node node){
		if(node.left == null){
			return node;
		}
		return miniNum(node.left);
	}
	
	//二分搜索树中最大的元素
	public E maxNum(){
		if(size == 0)
			throw new IllegalArgumentException("no node in bst.");
		return (E) maxNum(root).e;
	}
	
	private Node maxNum(Node node){
		if(node.right == null)
			return node;
		return maxNum(node.right);
	}
	
	//删除二分搜索树中最小的元素
	public E removeMiniNum(){
		E e = miniNum();
		removeMiniNum(root);
		return e;
	}
	
	private Node removeMiniNum(Node node) {
		if(node.left==null){
			Node rightNode = node.right;
			node.right=null;
			size--;
			return rightNode;
		}
		node.left = removeMiniNum(node.left);
		return node;
	}
	
	//删除最大的元素
	public E removeMax(){
		E max = maxNum();
		removeMax(root);
		return max;
	}
	
	//删除以node为根的树的最大节点(node.right=null)，并返回新的根
	private Node removeMax(Node node) {
		if(node.right==null){			//该节点为要删除的节点
			Node leftChild = node.left;
			node.left = null;
			size--;
			return leftChild;
		}
		node.right = removeMax(node.right);
		return node;
	}

	//删除某个元素
	public void remove(E e){
		remove(root,e);
	}
	
	//删除以node为根的树中的e
	private Node remove(Node node,E e){
		if(node==null)
			return node;
		
		if(e.compareTo((E) node.e)<0){
			node.left = remove(node.left,e);
		}else if(e.compareTo((E) node.e)>0){
			node.right=remove(node.right,e);
		}else{								 //node.e = e
			if(node.left==null){
				Node rightNode = node.right;
				node.right = null;
				size--;
				return rightNode;
			}else if(node.right==null){
				Node leftNode = node.left;
				node.left = null;
				size--;
				return leftNode;
			}
			//待删除的节点的左右子树均不为空
			Node successor = miniNum(node.right);
			successor.right = removeMiniNum(node.right);
			successor.left =  node.left;
			node.left = node.right = null;
			return successor; 
		}
		return null;
	}
}

  • 时间复杂度分析

增加一个元素时，需要逐一比较和节点的大小，每次进入左子树或者右子树，最复杂的情况是插入到树的最底层，时间复杂度和树的高度h是O（h）的关系，而对于一个满二叉树，BST中h和节点个数n的关系是n=2^h-1，则h=log2(n+1),所以时间复杂度为O(logn);同理，查询和删除也是这样的时间复杂度。

不要熬夜每一根头发都很珍贵
关注
  • 0
    点赞
  • 踩
  • 1
    收藏
    觉得还不错? 一键收藏
  • 0
    评论
python数据结构与算法详解与源码
08-20
数据结构与算法（Python） 一、引入概念 1-01算法引入 1-02 时间复杂度与大O表示法 1-03-最坏时间复杂度与计算规则 1-04-常见时间复杂度与大小关系 1-05-代码执行时间测量模块 1-06-Python列表类型不同操作的...
二分搜索树（Binary Search Tree）
qq_48019875的博客
11-22 2374
目录树结构一、为什么要有树结构二、二分搜索树的基础 树结构 一、为什么要有树结构 树结构本身是一种天然的组织结构 高效 二、二分搜索树的基础
数据结构与算法之二分搜索树
Admin_Lian的博客
03-06 278
目录(一) 定义(二) 自定义二分搜索树BinarySearchTree1. 新建自定义二分搜索树类BinarySearchTree2. 自定义二分搜索树的增加操作3. 自定义二分搜索树的查询操作4. 自定义二分搜索树的遍历操作5. 自定义二分搜索树的删除操作 (一) 定义 树(Tree): 是一种动态的数据结构. 它是由 n(n>=1) 个有限结点组成一个具有层次关系的集合. 也可...
前序、中序、后序遍历二分搜索树（遍历二分树）-java
test253506088的博客
09-08 228
之所以叫前序遍历是因为先访问左子树，之后遍历右子树，由于前序遍历的输出结果能完整的反应二分树的结构，所以一般使用前序遍历 /** * 二分搜索树,传入的泛型必须实现Comparable接口，保证具有可比较性 */ public class BinarySearchTree<E extends Comparable<E>> { private Node root;//根节点 private Integer size = 0; /** ...
二分搜索树
漫漫无期的博客
01-02 1596
二分搜索树（Binary Search Tree），也称为 二叉查找树 、二叉搜索树 、有序二叉树或排序二叉树。
算法之二分搜索树的建立和查找
weixin_42388255的博客
12-16 505
**二分搜索树（binary search tree)**是一种二叉树。每个结点的键值大于左孩子，每个结点的键值小于右孩子，以左右孩子为根的子树仍为二分搜索树。 二分搜索树不一定为完全二叉树，但是堆必须是完全二叉树。 建立二分搜索树的类代码： 二分搜索树插入新结点（insert） 二分搜索树的查找： 整段代码： //二分搜索树 key表示相对应得建，value表示数值。 template&...
数据结构C++描述
03-15
13.3.4 二分覆盖 415 13.3.5 单源最短路径 421 13.3.6 最小耗费生成树 424 13.4 参考及推荐读物 433 第14章 分而治之算法 434 14.1 算法思想 434 14.2 应用 440 14.2.1 残缺棋盘 440 14.2.2 归并排序 443 14.2.3 ...
数据结构算法与应用-C++语言描述
10-20
13.3.4 二分覆盖 415 13.3.5 单源最短路径 421 13.3.6 最小耗费生成树 424 13.4 参考及推荐读物 433 第14章 分而治之算法 434 14.1 算法思想 434 14.2 应用 440 14.2.1 残缺棋盘 440 14.2.2 归并排序 443 14.2.3 ...
数据结构与算法：C++描述
11-10
本书是关于计算机科学与工程领域的基础性研究科目之一——数据结构与算法的专著。 本书在简要回顾了基本的C++ 程序设计概念的基础上，全面系统地介绍了队列、堆栈、树、图等基本数据结构，以及贪婪算法、分而治之...
最优二分搜索树（动态规划）
11-17
设S=(x1,x2,…,xn)是有序集，且x1<x2<…<xn，已知键值和区间的存取概率分布为(a0,b1,a1,b2,…,bn,an)，其中ai表示相应区间的搜索概率，bi表示相应键值的搜索概率。在所有表示有序集的二叉树中找出一棵具有最小平均路长的二叉搜索树
python 二分叉查找
11-01
关于Python“二叉树”算法示例的代码
c++ 二分搜索树 二分查找树 binary search tree BST
11-24
c++ 二分搜索树 二分查找树 binary search tree BST
Java创建遍历二叉树（递归）并求树高及叶节点个数（代码全）
m0_55975991的博客
12-16 3566
二叉树的前序、中序、后序及层序全遍历方式，及递归求解树高（深度）和而叶子结点的个数全代码
【数据结构】二分搜索树
m0_50987960的博客
12-05 1250
自己创建的二叉搜索树的各种方法
二分搜索树的性质与实现
qq_22230709的博客
08-09 717
在讨论二分搜素树之前，我们先来讨论一下什么是二叉树 1.二叉树 二叉树和链表一样是一种动态的数据结构 a.二叉树：具有唯一的根节点 b.二叉树：每一个节点的左右子树也是二叉树，叶子节点的左右孩子都为null c.二叉树不一定是满的 d.一个节点也是二叉树 e.null 也是二叉树，也可以看成是一个链表 2.二分搜索树 Binary Search Tree 性质： ...
树结构-二分搜索树
土豆科技的博客
08-13 245
1.树的定义          树是一种数据结构，它是由n（n&gt;=1）个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的树,其中我们平常使用的目录就是常见的树;            1.1 二叉树的定义         在计算机科学中，二叉树是每个结点最多有两个子树的树结构。通常子树被称作“左子树”（left subtr...
算法入门---java语言实现的二分搜索树小结
宇你有缘
04-08 3116
图片均来自慕课网，仅仅为了学习记录。 1、二叉查找树（Binary Search Tree）      也可叫做二分查找树。它不仅可以查找数据，还可以高效地插入、删除数据。      特点：每个节点的key值大于左子节点，小于右子节点。注意它不一定是完全的二叉树。                所以节点的key是唯一的，我们就是通过它来索引key对应的value,注意图中标注的
怎么在KeilMDK里使用数据结构——树
最新发布
05-16
在这个示例代码中，我们首先定义了一个树节点结构体，包含了节点数据和左右子节点指针。然后我们定义了创建节点和插入节点的函数，使用递归的方式实现。最后我们定义了计算树深度的函数，并在main函数中使用。

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值