机器学习实战（一）：基于ID3的决策树手动实现（bagging集成）

最新推荐文章于 2025-12-16 15:16:39 发布

原创最新推荐文章于 2025-12-16 15:16:39 发布 · 993 阅读

21 ·

CC 4.0 BY-SA版权

文章标签：

#机器学习 #决策树 #人工智能

博客围绕鸢尾花分类问题展开，采用bagging方法和基于ID3的决策树算法。介绍了代码实现，包括数据读取、决策树构建、随机森林实现等函数。结果分析评估了基学习器数量和剪枝参数对泛化能力的影响，发现bagging能优化误分类率，剪枝对准确率提升不大。

1.题目解读

数据集采用经典的鸢尾花分类问题数据集如下：

序号	花萼长度	花萼宽度	花瓣长度	花瓣宽度	种类
1	5.1	3.5	1.4	0.2	setosa
2	4.9	3	1.4	0.2	setosa
3	4.7	3.2	1.3	0.2	setosa
4	4.6	3.1	1.5	0.2	setosa
5	5	3.6	1.4	0.2	setosa
6	5.4	3.9	1.7	0.4	setosa
7	4.6	3.4	1.4	0.3	setosa
8	5	3.4	1.5	0.2	setosa
9	4.4	2.9	1.4	0.2	setosa
10	4.9	3.1	1.5	0.1	setosa
11	5.4	3.7	1.5	0.2	setosa
12	4.8	3.4	1.6	0.2	setosa
13	4.8	3	1.4	0.1	setosa
14	4.3	3	1.1	0.1	setosa
15	5.8	4	1.2	0.2	setosa
16	5.7	4.4	1.5	0.4	setosa
17	5.4	3.9	1.3	0.4	setosa
18	5.1	3.5	1.4	0.3	setosa
19	5.7	3.8	1.7	0.3	setosa
20	5.1	3.8	1.5	0.3	setosa
21	5.4	3.4	1.7	0.2	setosa
22	5.1	3.7	1.5	0.4	setosa
23	4.6	3.6	1	0.2	setosa
24	5.1	3.3	1.7	0.5	setosa
25	4.8	3.4	1.9	0.2	setosa
26	5	3	1.6	0.2	setosa
27	5	3.4	1.6	0.4	setosa
28	5.2	3.5	1.5	0.2	setosa
29	5.2	3.4	1.4	0.2	setosa
30	4.7	3.2	1.6	0.2	setosa
31	4.8	3.1	1.6	0.2	setosa
32	5.4	3.4	1.5	0.4	setosa
33	5.2	4.1	1.5	0.1	setosa
34	5.5	4.2	1.4	0.2	setosa
35	4.9	3.1	1.5	0.2	setosa
36	5	3.2	1.2	0.2	setosa
37	5.5	3.5	1.3	0.2	setosa
38	4.9	3.6	1.4	0.1	setosa
39	4.4	3	1.3	0.2	setosa
40	5.1	3.4	1.5	0.2	setosa
41	5	3.5	1.3	0.3	setosa
42	4.5	2.3	1.3	0.3	setosa
43	4.4	3.2	1.3	0.2	setosa
44	5	3.5	1.6	0.6	setosa
45	5.1	3.8	1.9	0.4	setosa
46	4.8	3	1.4	0.3	setosa
47	5.1	3.8	1.6	0.2	setosa
48	4.6	3.2	1.4	0.2	setosa
49	5.3	3.7	1.5	0.2	setosa
50	5	3.3	1.4	0.2	setosa
51	7	3.2	4.7	1.4	versicolor
52	6.4	3.2	4.5	1.5	versicolor
53	6.9	3.1	4.9	1.5	versicolor
54	5.5	2.3	4	1.3	versicolor
55	6.5	2.8	4.6	1.5	versicolor
56	5.7	2.8	4.5	1.3	versicolor
57	6.3	3.3	4.7	1.6	versicolor
58	4.9	2.4	3.3	1	versicolor
59	6.6	2.9	4.6	1.3	versicolor
60	5.2	2.7	3.9	1.4	versicolor
61	5	2	3.5	1	versicolor
62	5.9	3	4.2	1.5	versicolor
63	6	2.2	4	1	versicolor
64	6.1	2.9	4.7	1.4	versicolor
65	5.6	2.9	3.6	1.3	versicolor
66	6.7	3.1	4.4	1.4	versicolor
67	5.6	3	4.5	1.5	versicolor
68	5.8	2.7	4.1	1	versicolor
69	6.2	2.2	4.5	1.5	versicolor
70	5.6	2.5	3.9	1.1	versicolor
71	5.9	3.2	4.8	1.8	versicolor
72	6.1	2.8	4	1.3	versicolor
73	6.3	2.5	4.9	1.5	versicolor
74	6.1	2.8	4.7	1.2	versicolor
75	6.4	2.9	4.3	1.3	versicolor
76	6.6	3	4.4	1.4	versicolor
77	6.8	2.8	4.8	1.4	versicolor
78	6.7	3	5	1.7	versicolor
79	6	2.9	4.5	1.5	versicolor
80	5.7	2.6	3.5	1	versicolor
81	5.5	2.4	3.8	1.1	versicolor
82	5.5	2.4	3.7	1	versicolor
83	5.8	2.7	3.9	1.2	versicolor
84	6	2.7	5.1	1.6	versicolor
85	5.4	3	4.5	1.5	versicolor
86	6	3.4	4.5	1.6	versicolor
87	6.7	3.1	4.7	1.5	versicolor
88	6.3	2.3	4.4	1.3	versicolor
89	5.6	3	4.1	1.3	versicolor
90	5.5	2.5	4	1.3	versicolor
91	5.5	2.6	4.4	1.2	versicolor
92	6.1	3	4.6	1.4	versicolor
93	5.8	2.6	4	1.2	versicolor
94	5	2.3	3.3	1	versicolor
95	5.6	2.7	4.2	1.3	versicolor
96	5.7	3	4.2	1.2	versicolor
97	5.7	2.9	4.2	1.3	versicolor
98	6.2	2.9	4.3	1.3	versicolor
99	5.1	2.5	3	1.1	versicolor
100	5.7	2.8	4.1	1.3	versicolor
101	6.3	3.3	6	2.5	virginica
102	5.8	2.7	5.1	1.9	virginica
103	7.1	3	5.9	2.1	virginica
104	6.3	2.9	5.6	1.8	virginica
105	6.5	3	5.8	2.2	virginica
106	7.6	3	6.6	2.1	virginica
107	4.9	2.5	4.5	1.7	virginica
108	7.3	2.9	6.3	1.8	virginica
109	6.7	2.5	5.8	1.8	virginica
110	7.2	3.6	6.1	2.5	virginica
111	6.5	3.2	5.1	2	virginica
112	6.4	2.7	5.3	1.9	virginica
113	6.8	3	5.5	2.1	virginica
114	5.7	2.5	5	2	virginica
115	5.8	2.8	5.1	2.4	virginica
116	6.4	3.2	5.3	2.3	virginica
117	6.5	3	5.5	1.8	virginica
118	7.7	3.8	6.7	2.2	virginica
119	7.7	2.6	6.9	2.3	virginica
120	6	2.2	5	1.5	virginica
121	6.9	3.2	5.7	2.3	virginica
122	5.6	2.8	4.9	2	virginica
123	7.7	2.8	6.7	2	virginica
124	6.3	2.7	4.9	1.8	virginica
125	6.7	3.3	5.7	2.1	virginica
126	7.2	3.2	6	1.8	virginica
127	6.2	2.8	4.8	1.8	virginica
128	6.1	3	4.9	1.8	virginica
129	6.4	2.8	5.6	2.1	virginica
130	7.2	3	5.8	1.6	virginica
131	7.4	2.8	6.1	1.9	virginica
132	7.9	3.8	6.4	2	virginica
133	6.4	2.8	5.6	2.2	virginica
134	6.3	2.8	5.1	1.5	virginica
135	6.1	2.6	5.6	1.4	virginica
136	7.7	3	6.1	2.3	virginica
137	6.3	3.4	5.6	2.4	virginica
138	6.4	3.1	5.5	1.8	virginica
139	6	3	4.8	1.8	virginica
140	6.9	3.1	5.4	2.1	virginica
141	6.7	3.1	5.6	2.4	virginica
142	6.9	3.1	5.1	2.3	virginica
143	5.8	2.7	5.1	1.9	virginica
144	6.8	3.2	5.9	2.3	virginica
145	6.7	3.3	5.7	2.5	virginica
146	6.7	3	5.2	2.3	virginica
147	6.3	2.5	5	1.9	virginica
148	6.5	3	5.2	2	virginica
149	6.2	3.4	5.4	2.3	virginica
150	5.9	3	5.1	1.8	virginica

2.思路分析

由于特征比较少（仅有4个），所有没有采取随机森林的标准方法，而是使用了bagging方法如下图。

其中先对于每一个基学习器，训练集通过自助采样法在原始数据集中进行采样获得，并将剩余数据作为测试集。（约37.2%）
基学习器算法采用基于ID3的决策树算法，具体如下图

其中信息增益率为

对决策树的剪枝采取后剪枝操作，具体如下：

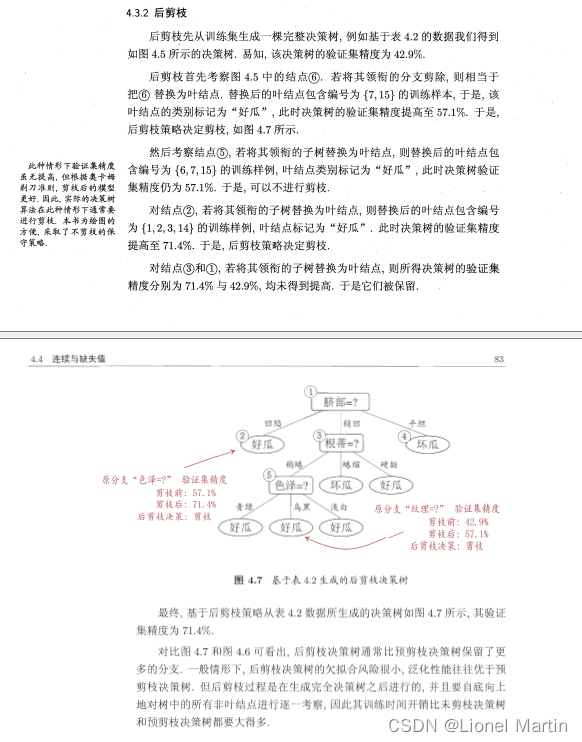
3.代码实现

主要由以下几个函数构成：

全局变量设置：
- NameSet：包含数据集中所有类别的集合。
- Name：类别名称与数字标识的映射。
- trans：数字标识与类别名称的映射。
数据读取与预处理：
- 使用pandas库读取CSV文件。
- 对数据进行标准化处理，以便于后续的计算。
决策树构建函数：
- calculate：计算给定数据集的最佳信息增益比。
- CreateTree：根据数据集创建决策树。
- check_part：递归检查决策树的每个节点。
- crosscheck：验证决策树的准确性。
- Simplify：简化决策树，进行剪枝。
- GetNodeNum：获取决策树的节点数。
- GetClassfier：获取分类器和验证集。
- NoPruning：创建决策树但不进行剪枝。
- left和right：获取决策树的左子树和右子树。
- seg_veridata：根据决策树分割验证数据集。
- Pruning：对决策树进行剪枝。
随机森林（Bagging）实现：
- Ensemble：集成多个分类器的预测结果。
- ErrorEstimate：估计分类器的错误率。
- bagging和bagging_nopruning：分别实现带剪枝和不带剪枝的随机森林。
- BaseLearner：生成一系列基学习器并计算它们的准确率。
参数设置与调整：
- SetParameter：设置决策树和随机森林的参数。
- SetRate：调整剪枝参数并计算准确率。
绘图与结果保存：
- draw_base：绘制基学习器数量与准确率的关系图。
- draw_rate：绘制剪枝参数与准确率的关系图。
- draw_prun：比较剪枝与不剪枝的准确率差异。
- 使用matplotlib库进行绘图，并保存图像。
- 使用pandas库将准确率数据保存为Excel文件。
代码执行与测试：
- 代码中包含了对上述函数的测试和示例执行。
- 通过调整参数和观察绘图结果来评估模型性能。

具体代码如下：

import pandas as pd
import numpy as np
import math
import matplotlib.pyplot as plt
import random
import string
from matplotlib import pyplot as plt

plt.rcParams['font.sans-serif'] = ['SimHei']  # 中文字体设置-黑体
plt.rcParams['axes.unicode_minus'] = False  # 解决保存图像是负号'-'显示为方块的问题


#全局变量设置
NameSet = {"setosa","versicolor","virginica"}
Name = {1:"setosa",2:"versicolor",3:"virginica"}
trans = {"setosa":1,"versicolor":2,"virginica":3}
#print(Name[1])
#读入数据
data = pd.read_csv("iris2.csv",header=None)
data = np.array(data)
data_copy = data
#print(data_copy)

num = len(data[:,5])
#对数据进行标准化处理

#参数设置
setrate = 0.2
bound = 0
T = 100
testnum = 10
PruningCheck = 1 

for i in range(0,len(data[:,5])):
    data[i][5] = trans[ data[i][5] ]
for i in range(1,5):
    Max = data[:,i].max()
    Min = data[:,i].min()
    for j in range(0,len(data[:,i])):
        data[j][i] = (Max - data[j][i]) / (Max - Min)

#给定数据集计算最佳信息增益比
def seg_data(seq,data):
    #print(seq)
    out = np.zeros((len(seq),6))
    for i in range(0,len(seq)):
        out[i,:] = data[int(seq[i]),:]
    return out

def calculate(data):
    if len(data[:,5]) <= 1:
        return "NULL"
    #计算信息增益比
    num = len(data[:,5])
    #计算H(D)
    
    cnt = [0]*4
    for i in range(0,num):
        data[i][5] = int(data[i][5])
    for i in range(0,num):
        cnt[ int(data[i][5]) ] += 1
    H_D = 0
    for i in range(1,4):
        if cnt[i] != 0:
            H_D += -(cnt[i]/num) * math.log2(cnt[i]/num)
    
    def Gain(j,t,data):
        num = len(data[:,5])
        stat = np.zeros((3,4))
        for i in range(0,num):
            if data[i][j] < t:
                tex = 1
            else:
                tex = 2
            stat[tex][ int(data[i][5]) ] += 1
        #print(stat)
        H_DA = 0 
        for k in range(1,3):
            tmp = 0
            for i in range(1,4):
                if stat[k][i] != 0:                    
                    tmp += -stat[k][i]/num * math.log2( stat[k][i]/num )
            tmp *= np.sum(stat[k,:])/num
            #print(np.sum(stat[k,:]))
            H_DA += tmp
        return H_D-H_DA
    
    GAIN = np.zeros(5)
    T = np.zeros(5)
    for i in range(1,5):
        #print(data[:,i])
        t_seq = np.sort(data[:,i])
        #print(t_seq)
        t_copy = [0] * ( len(t_seq) - 1 )
        for j in range(0,len(t_copy)):
            t_copy[j] = ( t_seq[j] + t_seq[j+1] ) / 2
        #print(t_copy)
        gain = [0] * len(t_copy)
        for j in range(0,len( t_copy )):
            gain[j] = Gain(i,t_copy[j],data)
            #print(t_copy[j], gain[j])
        #if np.size(gain) != 0:
        #if np.size(gain) < 10:
        #    print(data)
        """
        print(np.size(gain) )
        print(t_copy)
        print(gain)
        print(data)
        """
        tmp = np.argmax(gain)
        GAIN[i] = gain[tmp]
        T[i] = t_copy[tmp]
    seg_cate = np.argmax(T)
    seg_value = np.max(T)
    info_increase = np.max(GAIN)
    seq_low = []
    seq_high = []
    for i in range(0,num):
        if data[i][seg_cate] < seg_value:
            seq_low += [i]
        else:
            seq_high += [i]
    data_low = seg_data(seq_low,data)
    data_high = seg_data(seq_high,data)
    cnt = np.zeros(4)
    for i in range(0,len(data)):
        cnt[ int(data[i][5]) ] += 1
    most_cate = np.argmax(cnt)
    output = (seg_cate,seg_value,info_increase,data_low,data_high,most_cate)
    return output
    #print(GAIN,T)
#定义信息增益阈值
#bound = 0
def CreateTree(data):
    #检测是否类标签相同
    for i in range(1,len(data)):
        if data[i][5] != data[i-1][5]:
            break
        if i == len(data) - 1:
            return Name[ data[i][5] ]
    seg = calculate(data)
    #print(seg[0:3],seg[5])
    #print( np.size(seg[3]) , np.size(seg[4]) )
    if seg == "NULL":
        return Name[data[0][5]]
    if np.size(seg[3]) * np.size(seg[4]) == 0:
        return Name [ seg[5] ]
    if seg[2] < bound:
        return Name[ seg[5] ]
    mytree = { seg[0] :{round(seg[1],2):{ "fir":CreateTree(seg[3]),"sec":CreateTree(seg[4])} } }
    return mytree
#mytree = CreateTree(data)
#print(mytree)
def check_part(mytree,test):
    #print(mytree)
    if type(mytree) == type("setosa"):
        return mytree
    key =  list( mytree.keys() )
    cate = key[0]
    cate_key = list ( mytree[ cate ] .keys() )
    seg = cate_key[0]
    #print(test,seg)
    if test[ cate ] < seg:
        mytree = mytree[ cate ][ seg ][ 'fir' ]
    else:
        mytree = mytree[ cate ][ seg ][ 'sec' ]
    #print(type(mytree))
    if type(mytree) == type("str"):
        return mytree
    return check_part ( mytree,test )
def crosscheck(mytree,data):
    #print(mytree)
    #print(data)
    num = len(data[:,5])
    #print("num=",num)
    cnt = 0
    for i in range(0,num):
        res = check_part(mytree,data[i,:])
        #print(res,data[i][5])
        if res == Name[ int(data[i][5]) ]:
            cnt += 1
    return cnt
#设置基于Bagging的训练轮数T
#T = 50
def Simplify(mytree):
    if type(mytree) == type("setosa"):
        return mytree
    key =  list( mytree.keys() )
    cate = key[0]
    cate_key = list ( mytree[ cate ] .keys() )
    seg = cate_key[0]
    if type(mytree[ cate ][ seg ][ 'fir' ]) != type("setosa"):
        mytree[ cate ][ seg ][ 'fir'] = Simplify( mytree[ cate ][ seg ][ 'fir'] )
    if type(mytree[ cate ][ seg ][ 'sec' ]) != type("setosa"):
        mytree[ cate ][ seg ][ 'sec' ] = Simplify( mytree[ cate ][ seg ][ 'sec'] )
    if type(mytree[ cate ][ seg ][ 'fir' ]) == type("setosa") and type(mytree[ cate ][ seg ][ 'sec' ]) == type("setosa") and mytree[ cate ][ seg ][ 'fir' ] ==  mytree[ cate ][ seg ][ 'sec' ]:
        mytree =  mytree[ cate ][ seg ][ 'fir' ]
        return mytree
    return mytree
def GetNodeNum(mytree):
    if type(mytree) == type("setosa"):
        return 0
    key =  list( mytree.keys() )
    cate = key[0]
    cate_key = list ( mytree[ cate ] .keys() )
    seg = cate_key[0]
    cnt = 1
    #if type(mytree[ cate ][ seg ][ 'fir' ]) != type("setosa"):
    cnt += GetNodeNum( mytree[ cate ][ seg ][ 'fir'] )
    #if type(mytree[ cate ][ seg ][ 'sec' ]) != type("setosa"):
    cnt += GetNodeNum( mytree[ cate ][ seg ][ 'sec'] )
    return cnt
def GetClassfier(data):
    num = len(data[:,5])
    data_seq = np.zeros(num)
    for i in range(0,num):
        tmp = random.randint(0,num-1)
        data_seq[i] = tmp
    tmp = []
    for i in range(0,num):
        if i not in data_seq:
            tmp.append(i)
    veri_seq = np.array(tmp)
    dataset = seg_data(data_seq,data)
    #print(len(tmp))
    veriset = seg_data(veri_seq,data)
    #print("veriset=",veriset)
    mytree = CreateTree(dataset)
    #print("old=",mytree)
    mytree = Simplify(mytree)
    if PruningCheck == 1:
       mytree = Pruning(mytree,veriset)
    #print("nodenum=",GetNodeNum(mytree),"mytree=",mytree)
    return (mytree,veri_seq)
def NoPruning(data):
    num = len(data[:,5])
    data_seq = np.zeros(num)
    for i in range(0,num):
        tmp = random.randint(0,num-1)
        data_seq[i] = tmp
    tmp = []
    for i in range(0,num):
        if i not in data_seq:
            tmp.append(i)
    veri_seq = np.array(tmp)
    dataset = seg_data(data_seq,data)
    #print(len(tmp))
    veriset = seg_data(veri_seq,data)
    #print("veriset=",veriset)
    mytree = CreateTree(dataset)
    #print("old=",mytree)
    mytree = Simplify(mytree)
    #mytree = Pruning(mytree,veriset)
    #print("nodenum=",GetNodeNum(mytree),"mytree=",mytree)
    return (mytree,veri_seq)
def left(mytree):
    key =  list( mytree.keys() )
    cate = key[0]
    cate_key = list ( mytree[ cate ] .keys() )
    seg = cate_key[0]
    return mytree[ cate ][ seg ][ 'fir']
def right(mytree):
    key =  list( mytree.keys() )
    cate = key[0]
    cate_key = list ( mytree[ cate ] .keys() )
    seg = cate_key[0]
    return mytree[ cate ][ seg ][ 'sec']
def seg_veridata(mytree,data):
    key =  list( mytree.keys() )
    cate = key[0]
    cate_key = list ( mytree[ cate ] .keys() )
    seg = cate_key[0]
    leftseq = []
    rightseq = []
    num = len(data[:,5])
    for i in range(0,num):
        if data[ i ][ cate ] < seg:
            leftseq += [i]
        else:
            rightseq += [i]
    leftdata = seg_data(leftseq,data)
    rightdata = seg_data(rightseq,data)
    return (leftdata,rightdata)
def Pruning(mytree,data):
    num = len(data[:,5])
    if type(mytree) == type("str") or num == 0:
        return mytree
    key =  list( mytree.keys() )
    cate = key[0]
    cate_key = list ( mytree[ cate ] .keys() )
    seg = cate_key[0]
    res = seg_veridata(mytree, data)
    leftdata = res[0]
    rightdata = res[1]
    mytree[ cate ][ seg ][ 'fir'] = Pruning( left(mytree) , leftdata)
    mytree[ cate ][ seg ][ 'sec'] = Pruning( right(mytree) , rightdata)
    unpruning_rate = crosscheck(mytree,data)/num
    cnt = np.zeros(4)
    for i in range(0,num):
        #print(data[i][5])
        cnt[ int(data[i][5]) ] += 1
    pruning_rate = np.max(cnt)/num
   # print(cnt,"num=",num,"mytree=",mytree)
    pruning_name = Name[ np.argmax(cnt) ]
    if pruning_rate - unpruning_rate > setrate:
        mytree = pruning_name
    return mytree
def Ensemble(classfier,data_setlist,test):
    cnt = np.zeros(4)
    for i in range(0,T):
        if test[0] not in data_setlist[i]:
            #print( check_part( classfier[i] , test ) )
            cnt[ trans[ check_part( classfier[i] , test ) ] ]+= 1
    print(cnt)
    return np.argmax(cnt)
def ErrorEstimate(classfier,data_setlist,data):
    num = len(data[:,5])
    cnt = 0
    for i in range(0,num):
        if Ensemble(classfier,data_setlist, data[i,:] ) == data[i][5]:
            cnt += 1
    return cnt/num
def bagging(data):
    classfier = [0] * T
    data_setlist = [0] * T
    for i in range(0,T):
        res = GetClassfier(data)
        #print(i)
        classfier[i] = res[0]
        data_setlist[i] = res[1]
    
    #print(mytree)
    #print("check")
    error = ErrorEstimate(classfier,data_setlist,data)
    return error
#bagging(data)
def bagging_nopruning(data):
    classfier = [0] * T
    data_setlist = [0] * T
    for i in range(0,T):
        res = NoPruning(data)
        #print(i)
        classfier[i] = res[0]
        data_setlist[i] = res[1]
    
    #print(mytree)
    #print("check")
    error = ErrorEstimate(classfier,data_setlist,data)
    return error
nopruning = np.zeros(10)
pruning = np.zeros(10)
"""
for i in range(0,testnum):
    nopruning[i] = bagging_nopruning(data)
    pruning[i] = bagging(data)
    print("nopruning=",nopruning[i],"pruning=",pruning[i],"delta=",pruning[i]-nopruning[i])
print("avg_delta=",(np.sum(pruning)-np.sum(nopruning))/testnum)
"""


setrate = 0
bound = 0
T = 100
testnum = 10
PruningCheck = 1

Parameter = [0.2,0,100,10,1]
def SetParameter(Parameter):
    global setrate
    global bound
    global T
    global testnum
    global PruningCheck
    setrate = Parameter[0]
    bound = Parameter[1]
    T = Parameter[2]
    testsnum = Parameter[3]
    PruningCheck = Parameter[4]

Ques = [
        [0,5.9,2.6,3.8,1.2],
        [0,6.1,2.6,5.3,1.7],
        [0,5.1,3.5,1.4,0.2],
        [0,7.2,3.6,6.1,2.5]
        ]

tmp = pd.read_csv("iris2.csv",header=None)
data_copy = np.array(tmp)
#print(data_copy)

for i in range(0,len(Ques)):
    for j in range(1,5):
        #print(data_copy)
        max_data = np.max(data_copy[:,j])
        min_data = np.min(data_copy[:,j])
        #print(data_copy[:,j])
        #print(max_data,min_data)
        Ques[i][j] = (max_data - Ques[i][j]) / (max_data - min_data)
#print(Ques)
classifier = [0] * T
for i in range(0,T):
    res = GetClassfier(data)
    classifier[i] = res[0]
dataset = [] 
for i in range(0,T):
    dataset.append([])
#print(dataset)
for i in range(0,len(Ques)):
    print( "第"+str(i+1)+"支花的类别是:",Name[ Ensemble(classifier, dataset, Ques[i] ) ]  )
        

def PerformanceAnalysis(data):
    Parameter = [0.2,0,10,10,1]
    SetParameter(Parameter)
    Total_T = 10
    def BaseLearner(Total_T):
        bagging_data = np.zeros(Total_T)
        for i in range(1,Total_T + 1):
            print(i)
            Parameter[2] = i
            SetParameter(Parameter)
            #print("T=",T)
            bagging_data[i-1] = bagging(data)
            #print(i,bagging_data[i-1])
        return bagging_data
    
    bagging_data = BaseLearner(Total_T)
    
    
    x=range(1,Total_T + 1)
    #设置y
    y=bagging_data
    #plot函数需要两个参数，一个是x一个是y
    def draw_base(x,y):
        plt.plot(x,y,"ob:")
        plt.title('基学习器数量和准确率的关系图')
        plt.xlabel('基学习器数量')
        plt.ylabel('准确率')
        plt.legend()
    draw_base(x,y)
    plt.show()
    draw_base(x,y)
    plt.savefig('基学习器数量对准确率的影响.png')
    op = pd.DataFrame(y)
    #op.to_excel('y.xlsx')
    Parameter = [0.2,0,10,10,1]
    
    
    
    def SetRate(maxrate):
        bagging_data = np.zeros(int(maxrate/min_step + 1))
        y_unpruning = np.zeros(int(maxrate/min_step + 1))
        for i in np.arange(0,maxrate+min_step,min_step):
            Parameter[0] = i
            PruningCheck = 1
            SetParameter(Parameter)
            #print("setrate=",setrate)
            bagging_data[ int(i/min_step) ] = bagging(data)
            PruningCheck = 0
            y_unpruning[ int(i/min_step) ] = bagging(data)
            print(i,bagging_data[ int(i/min_step) ],y_unpruning[ int(i/min_step) ])
            #print("setrate=",setrate,bagging_data[ int(i/min_step) ])
        return (bagging_data,y_unpruning)
    def draw_rate(x,y,y_unpruning):
        #plt.plot(x,y,"ob:")
        
        plt.plot(x,y,"ob:",label="pruning")
        plt.plot(x,y_unpruning,"or:",label="unpruning")
        
        plt.title('剪枝参数和准确率的关系图')
        plt.xlabel('剪枝参数')
        plt.ylabel('准确率')
        plt.legend()
    min_step = 0.02
    maxrate = 0.1
    res = SetRate(maxrate)
    x = np.arange(0,maxrate+min_step,min_step)
    #print(x)
    #print(np.size(x))
    #设置y
    y = res[0]
    y_unpruning = res[1]
    draw_rate(x,y,y_unpruning)
    plt.show()
    draw_rate(x,y,y_unpruning)
    plt.savefig('剪枝参数对准确率的影响.png')
    
    out = np.zeros((2, np.size(y) ))
    out[0,:] = y
    out[1,:] = y_unpruning
    op = pd.DataFrame(out)
    #op.to_excel('pruning or not.xlsx')
    
#PerformanceAnalysis(data)
"""
"""
"""
Parameter = [0.2,0,10,10,1]
SetParameter(Parameter)
num_set = 5
x = range(1,num_set + 1)
y_pruning = np.zeros(num_set)
y_unpruning = np.zeros(num_set)
for i in range(0,num_set):
    PruningCheck = 1
    y_pruning[i] = bagging(data)
    PruningCheck = 0
    y_unpruning[i] = bagging(data)
print("剪枝平均单次误差提升",( np.sum(y_pruning)-np.sum(y_unpruning) ) / num_set)
def draw_prun():
    plt.plot(x,y_pruning,"ob:",label="pruning")
    plt.plot(x,y_unpruning,"or:",label="unpruning")
    plt.title('剪枝参数和准确率的关系图')
    plt.xlabel('次数')
    plt.ylabel('准确率')
    plt.legend()
draw_prun()
plt.show()
draw_prun()
plt.savefig('是否剪枝对准确率的影响.png')
#create_plot(mytree)
#op = pd.DataFrame(data)
#op.to_excel('data1.xlsx')
"""  
#基于ID3算法实现决策树构建

"""
"""
{3: {0.75: {'fir': {2: {0.81: {'fir': {2: {0.73: {'fir': {2: {0.69: {'fir': {2: {0.6: {'fir': {1: {0.54: {'fir': {1: {0.49: {'fir': {3: {0.31: {'fir': 'virginica', 
                                                                                                                                                'sec': 'versicolor'}}}, 
                                                                                                                             'sec': 'versicolor'}}}, 
                                                                                                          'sec': 'versicolor'}}}, 
                                                                                       'sec': {2: {0.65: {'fir': 'versicolor', 
                                                                                                          'sec': 'virginica'}}}}}}, 
                                                                     'sec': 'versicolor'}}}, 
                                                  'sec': {2: {0.77: {'fir': 'versicolor', 'sec': 'versicolor'}}}}}}, 
                               'sec': 'versicolor'}}}, 
            'sec': 'setosa'}}}
"""
"""

4.结果分析

主要通过由以下几个部分构成：
1. 评估基学习器数量对于泛化能力的提升
2. 评估剪枝参数和是否剪枝对于泛化能力的提升
这里先对几个重要参数做说明：
Setrate（）表示剪枝容忍度，即对于用于包外剪枝的数据集，如果将一棵树直接换成判断节点比原来的树的准确度好Setrate时就决定剪枝。
T 表示基学习器数量，即使用几个基学习器参与投票进行分类
PruningCheck 表示是否剪枝，0代表不剪枝，1代表剪枝。
通过运行程序，我们可以获得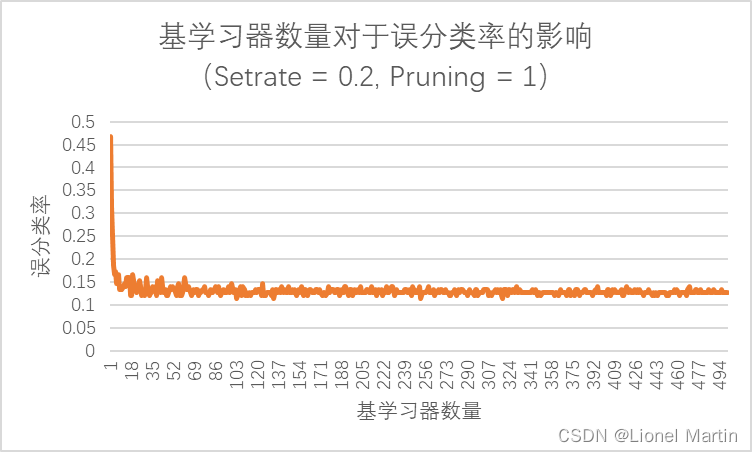

观察图片可知bagging集成技术对于误分类率的优化是现象级的，当T=1时，ER (ErrorRate) = 46.67%. 但是当T=20时，ER = 14%. 但是当基学习器大幅度增加时，误分类率未见明显增长基本稳定在13%左右，即
分类准确率 = 87%

分析剪枝参数对于准确率的影响我们有以下图片：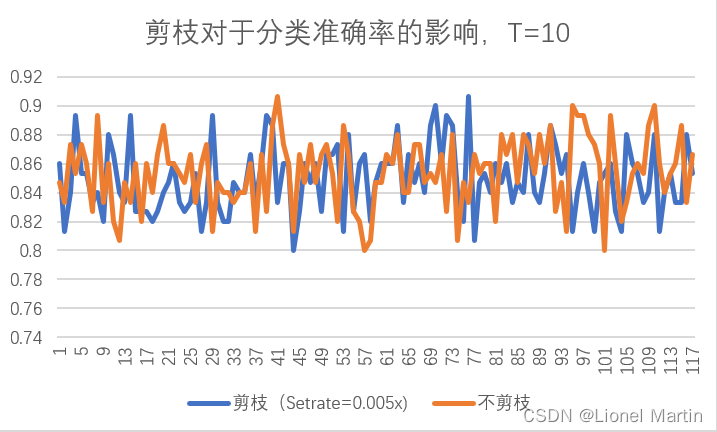
其中Setrate从0按步长0.005逐渐变化到0.6
剪枝平均准确率   0.834958
不剪枝平均准确率   0.846779
相对差值   -0.01182
分析可知，平均来说，剪枝准确率甚至比不剪枝的平均准确率还少了约1%，但结合图像变化，可以认为，剪枝操作对准确率的提升不大。