协同过滤算法_eulidsim-CSDN博客

本文链接：https://blog.csdn.net/bigbigship/article/details/51050301

协同过滤简介

协同过滤是一种基于一组兴趣相同的用户或项目进行的推荐，它根据邻居用户(与目标用户兴趣相似的用户)的偏好信息产生对目标用户的推荐列表。
协同过滤算法主要分为：

基于用户的协同过滤算法
基于物品的协同过滤算法

基于用户的协同过滤算法

基于用户的协同过滤算法是根据邻居用户的偏好信息产生对目标用户的推荐。它基于这样一个假设:如果一些用户对某一类项目的打分比较接近，则他们对其它类项目的打分也比较接近。协同过滤推荐系统采用统计计算方式搜索目标用户的相似用户，并根据相似用户对项目的打分来预测目标用户对指定项目的评分，最后选择相似度较高的前若干个相似用户的评分作为推荐结果，并反馈给用户。

基于物品的协同过滤算法

基于物品的协同过滤是根据用户对相似物品的评分数据预测目标项目的评分，它是建立在如下假设基础上的:如果大部分用户对某些物品的打分比较相近，则当前用户对这些项的打分也会比较接近。ltem一based协同过滤算法主要对目标用户所评价的一组项目进行研究，并计算这些项目与目标项目之间的相似性，然后从选择前K个最相似度最大的项目输出，这是区别于User-based协同过滤。

相似度计算

欧式距离

设向量 $A=\{a_1,a_2,...,a_n\}$ , $B=\{b_1,b_2,...,b_n\}$
$distance = \sqrt{\Sigma_{i=1}^n(a_i-b_i)^2}$
$similartiy = \frac{1}{1+distance}$

皮尔逊相关系数

皮尔逊相关系数是一种度量两个变量间相关程度的方法。它是一个介于 1 和 -1 之间的值，其中，1 表示变量完全正相关， 0 表示无关，-1 表示完全负相关。

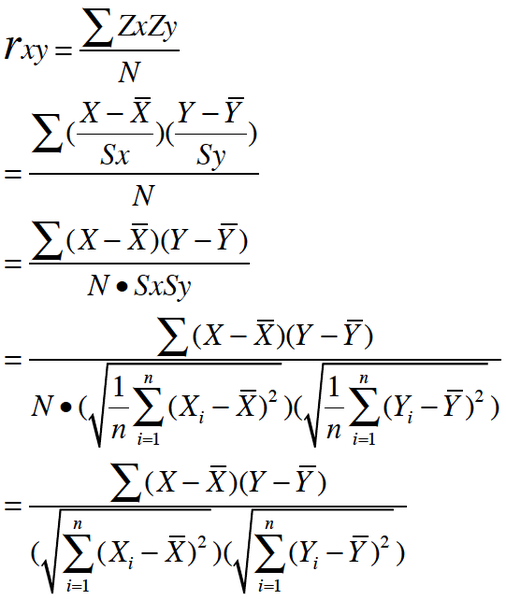
按照高中数学水平来理解, 它很简单, 可以看做将两组数据首先做Z分数处理之后, 然后两组数据的乘积和除以样本数。
Z分数一般代表正态分布中, 数据偏离中心点的距离.等于变量减掉平均数再除以标准差.(就是高考的标准分类似的处理)
标准差则等于变量减掉平均数的平方和,再除以样本数,最后再开方.
皮尔逊相关的约束条件

从以上解释, 也可以理解皮尔逊相关的约束条件:

两个变量间有线性关系
变量是连续变量
变量均符合正态分布,且二元分布也符合正态分布
两变量独立

余弦相似度

余弦相似度计算的是两个向量夹角的余弦值。若夹角为90度则相似度为0，若两个向量的方向相同，则相似度为1。余弦相似度的取值范围为[-1,1],因此我们也将它们归一化到[0,1]。

c o s θ = A * B | | A | | * | | B | |

$cos\theta = \frac{A*B}{||A||*||B||}$

两种算法的比较

当物品的数据相对稳定，例如电子商务类型的网站，计算相似度的计算量相对较小，同时不必频繁更新，因此可以使用基于物品的协同过滤算法，但是对于新闻，博客等更新较快的系统,物品的数量是海量的，计算更加复杂，因此我们需要使用基于用户的协同过滤算法。

用户	鳗鱼饭	鸡排	寿司	烤牛肉	手撕猪肉
Jim	2	0	0	4	4
John	5	5	5	3	3
Sally	2	4	2	1	2

参考上表，行与行之间的比较是基于用户的相似度，列与列之间的比较则是基于武平的相似度，到底使用哪一种相似度，这取决与用户或者物品的数量。

实例：餐馆菜肴推荐引擎

svdRec.py

#-*-coding=utf-8 -*-
from numpy import *
from numpy import linalg as la
def loadExData():
    return [[1,1,1,0,0],
             [2,2,2,0,0],
             [1,1,1,0,0],
             [5,5,5,0,0],
             [1,1,0,2,2],
             [0,0,0,3,3],
             [0,0,0,1,1]]

#计算欧几里得相似度
def eulidSim(inA,inB):
    return 1.0/(1.0+la.norm(inA-inB))
#计算皮尔逊相似度
def pearsSim(inA,inB):
    if len(inA)<3:
        return 1.0
    return 0.5+0.5*corrcoef(inA,inB,rowvar=0)[0][1]

#计算余弦相似度
def cosSim(inA,inB):
    num= float(inA.T*inB)
    denom = la.norm(inA)*la.norm(inB)
    return 0.5+0.5*(num/denom)
#计算在给定相似度计算方法下，用户对物品的估计评分值
def standEst(dataMat,user,simMeas,item):
    n = shape(dataMat)[1]
    simTotal = 0.0
    ratSimTotal =0.0
    for j in range(n):
        userRating = dataMat[user,j]
        if userRating == 0:
            continue;
        overlap = nonzero(logical_and(dataMat[:,item].A>0,dataMat[:,j].A>0))[0]
        if len(overlap) == 0:
            similarity=0
        else:
            similarity = simMeas(dataMat[overlap,item],dataMat[overlap,j])
        simTotal += similarity
        ratSimTotal += similarity*userRating
    if simTotal == 0:
        return 0.0
    else:
        return ratSimTotal/simTotal

def recommend(dataMat,user,N=3,simMeas=cosSim,estMethod=standEst):
    unratedItems = nonzero(dataMat[user,:].A==0)[1] #find the item which the user not ranked
    if len(unratedItems) == 0:
        return "you rated everything"
    itemScore = []
    for item in unratedItems:
        estimatedScore = estMethod(dataMat,user,simMeas,item)
        itemScore.append((item,estimatedScore))
    return sorted(itemScore,key=lambda jj : jj[1] ,reverse=True)[:N]

Restaurant_recommendation_system.py

#-*-coding=utf-8 -*-
from  numpy import *
from matplotlib import *
import svdRec
mymat = mat(svdRec.loadExData())
"""
testing Sim
print svdRec.eulidSim(mymat[:,0],mymat[:,4])
print svdRec.eulidSim(mymat[:,0],mymat[:,0])
print svdRec.cosSim(mymat[:,0],mymat[:,0])
print svdRec.cosSim(mymat[:,0],mymat[:,4])
print svdRec.pearsSim(mymat[:,0],mymat[:,4])
print svdRec.pearsSim(mymat[:,0],mymat[:,0])
"""
"""
testing predict
"""
print mymat
mymat[0,1]=mymat[0,0]=mymat[1,0]=mymat[2,0]=4
mymat[3,3]=2
print mymat
print svdRec.recommend(mymat,2)