4.1 卷积神经网络（CV简述、卷积运算（滤波器、边缘检测）、填充padding、高维卷积（3维的RGB图片进行卷积运算）、单层卷积网络与传统神经网络对比、池化层、使用卷积的原因）

本文链接：https://blog.csdn.net/bijingrui/article/details/108671958

本文介绍了卷积神经网络的基本概念，包括卷积运算、边缘检测、填充和步长等核心内容，并探讨了如何通过卷积层、池化层和全连接层构建卷积神经网络。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

计算机视觉

一般的计算机视觉问题包括以下几类：

图片分类（Image Classification）；
目标检测（Object detection）；
神经风格转换（Neural Style Transfer）。

输入可能会非常大

之前处理的是64*64*3的图片，但是一张 1000x1000x3 的图片，神经网络输入层（第0层）就是300W个神经元，更别说 W 非常大。

导致：

神经网络结构复杂，数据量相对较少，容易出现过拟合；
所需内存和计算量巨大。

因此，一般的神经网络很难处理蕴含着大量数据的图像。

解决这一问题的方法就是使用卷积神经网络（Convolutional Neural Network, CNN）。

卷积运算

简述

神经网络由浅层到深层，分别可以检测出图片的边缘特征、局部特征（例如眼睛、鼻子等），到最后面的一层就可以根据前面检测的特征来识别整体面部轮廓。这些工作都是依托卷积神经网络来实现的。
卷积运算（Convolutional Operation）是卷积神经网络最基本的组成部分。

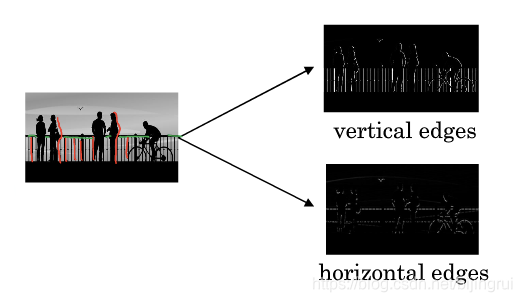
边缘检测

两类

垂直边缘（Vertical Edges）检测和水平边缘（Horizontal Edges）检测。

# 依据不同的滤波器来实现。

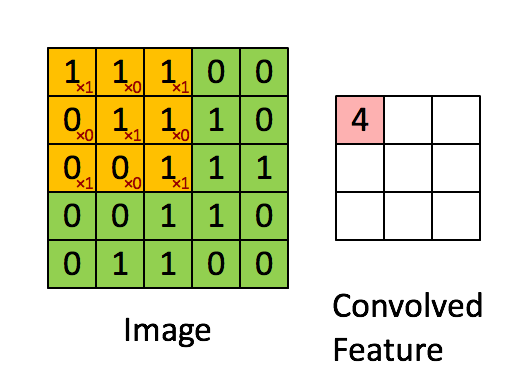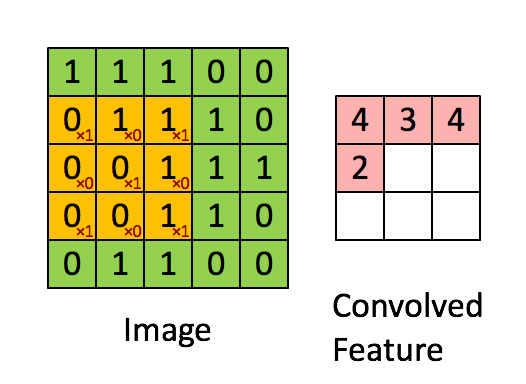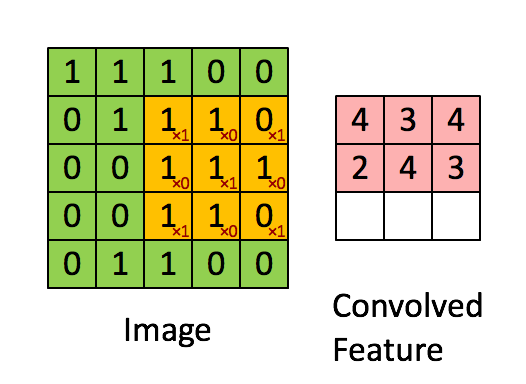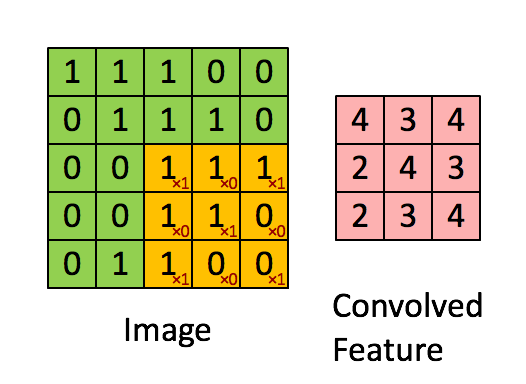
卷积运算的方式

# 注释： * 号代表的含义不是矩阵相乘，也不是元素相乘，* 就是卷积的标准符号！

垂直边缘检测

1 == 白色

0 == 灰色

-1 == 黑色

水平边缘检测

其他滤波器

参数

滤波器中的值还可以设置为参数w，通过模型训练来得到。

这样，神经网络使用反向传播算法可以学习到一些低级特征，从而实现对图片所有边缘特征的检测，而不仅限于垂直边缘和水平边缘。

填充(padding)

两个问题

图片缩小

假设输入图片的大小为 6×6，而滤波器的大小为 3×3，则卷积后的输出图片大小为 (6−3+1)×(6−3+1)。

假设输入图片的大小为 n×n，而滤波器的大小为 f×f，则卷积后的输出图片大小为 (n−f+1)×(n−f+1)。

细节丢失

解决方案：padding

设每个方向扩展像素点数量为 p，则填充后原始图片的大小为 (n+2p)×(n+2p)，滤波器大小保持 f×f不变，则输出图片大小为 (n+2p−f+1)×(n+2p−f+1)。

卷积步长

简述

步长 == 滤波器在原始图片上每次移动的距离。

之前，步长被默认为 1。而如果我们设置步长为 2，则：

公式

设步长为 s，填充长度为 p，原始图片大小为 n * n，滤波器大小为 f * f，则卷积后图片的尺寸为：

（向下取整）

高维卷积（3维的RGB图片进行卷积运算）

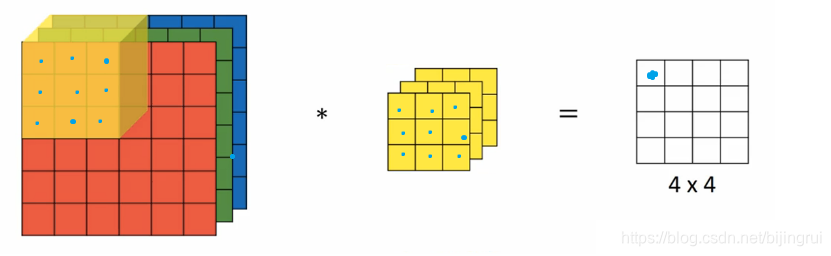
如果我们想要对3通道的 RGB 图片进行卷积运算，那么其对应的滤波器组也同样是3通道的。

过程是：原始图片的每一层（选定部分）分别与滤波器对应层 做卷积运算，最终结果 == add（第一层结果,第二层结果，第三层结果），即：27 个乘积结果的和 == 输出图片的一个像素值。

不同通道的滤波器可以不相同。例如只检测 R 通道的垂直边缘，G 通道和 B 通道不进行边缘检测，则 G 通道和 B 通道的滤波器全部置零。当输入有特定的高、宽和通道数时，滤波器可以有不同的高和宽，但通道数必须与输入一致。

单层卷积网络

前向传播

对于一个 3x3x3 的滤波器，包括偏移量 b在内共有 28 个参数。

不论输入的图片有多大，用这一个滤波器来提取特征时，参数始终都是 28 个，固定不变。

即选定滤波器组后，参数的数目与输入图片的尺寸无关。

因此，卷积神经网络的参数相较于标准神经网络来说要少得多。这是 CNN 的优点之一。

符号总结

对于w维度的注释：

为什么

因为：一个滤波器（3维） == ，并且一共有

参考：

# 有些作者会将通道数放在首位，需要根据标示自行分辨

一个简单的卷积神经网络的例子

# 注释：

上图只说了f[l] * f[l]，而第三个维度：通道数与上张图片的通道数是一致的，滤波器维度应该是 f[l] * f[l] * nc[l-1]

这样一个滤波器正方体==出一张图，一共有 20个滤波器正方体，就出20张图，一定要想好这个

一个典型的卷积神经网络通常包含有三种层：

卷积层（Convolution layer）
池化层（Pooling layer）
全连接层（Fully Connected layer）。

仅用卷积层也有可能构建出很好的神经网络，但大部分神经网络还是会添加池化层和全连接层，它们更容易设计。

池化层

作用：

缩减模型的大小
提高计算速度
减小噪声
提高所提取特征的稳健性（鲁棒性）

一种池化过程：最大池化（Max Pooling）

将输入拆分成不同的区域，输出的每个元素都是对应区域中元素的最大值，（就像从远处看一张图）：

池化过程类似于卷积过程 == 类似于使用了一个大小 f=2 步长 s=2 的滤波器（并没有卷积计算，只是选了个最大的），如果有多个通道，那么就对每个通道分别执行计算过程。

元素值较大可能意味着池化过程之前的卷积过程提取到了某些特定的特征，池化过程中的最大化操作使得只要在一个区域内提取到某个特征，它都会保留在最大池化的输出中。但是，没有足够的证据证明这种直观解释的正确性，而最大池化被使用的主要原因是它在很多实验中的效果都很好。

另一种池化过程：平均池化（Average Pooling）

从取某个区域的最大值改为求这个区域的平均值

特点

它有一组超参数，但是并没有参数需要学习。池化过程的超参数包括滤波器的大小 f、步长 s，以及选用最大池化/平均池化。而填充 p则很少用到。（因为所有元素都遍历了，找最大而已，不需要padding）

卷积神经网络示例

# 用来直观感受的网站https://www.cs.ryerson.ca/~aharley/vis/conv/

使用卷积的原因

相比标准神经网络，对于大量的输入数据，卷积过程有效地减少了 CNN 的参数数量，原因有以下两点：

参数共享（Parameter sharing）：特征检测如果适用于图片的某个区域，那么它也可能适用于图片的其他区域。即在卷积过程中，不管输入有多大，一个特征探测器（滤波器）就能对整个输入的某一特征进行探测。
稀疏连接（Sparsity of connections）：在每一层中，由于滤波器的尺寸限制，输入和输出之间的连接是稀疏的，每个输出值只取决于输入在局部的一小部分值。（如果不用卷积，小小一张图就1400W个参数，这还是一张小图而已）

池化过程则在卷积后很好地聚合了特征，通过降维来减少运算量。

由于 CNN 参数数量较小，所需的训练样本就相对较少，因此在一定程度上不容易发生过拟合现象。并且 CNN 比较擅长捕捉区域位置偏移。即进行物体检测时，不太受物体在图片中位置的影响，增加检测的准确性和系统的健壮性。