一.概述
树状数组的特点,一句话就是:定点更新,区间求值。例如,数组{a}中的元素可能不断地被修改,它能够高效地获取数组中连续n个数的和。数据规模不大的时候,对于修改某点的值是非常容易的,复杂度是O(1),但是对于求一个区间的和就要扫一遍了,复杂度是O(N),如果实时的对数组进行M次修改或求和,最坏的情况下复杂度是O(M*N).而用树状数组的复杂度却是O(M*lgN),别小看这个lg,当数据规模很大的时候,效率就大大提升了。
二.基本操作
传统数组(共n个元素)的元素修改和连续元素求和的复杂度分别为O(1)和O(n)。树状数组通过将线性结构转换成伪树状结构(线性结构只能逐个扫描元素,而树状结构可以实现跳跃式扫描),使得修改和求和复杂度均为O(lgn),大大提高了整体效率。

A数组就是我们要维护和查询的数组,但是其实我们整个过程中根本用不到A数组!C数组才是我们全程关心和操纵的重心。先由图来看看c数组的规则,其中c8 = c4+c6+c7+a8,c6 = c5+a6……
怎么做到的?解释如下:给定序列(数列)A,我们设一个数组C满足
C[i] = A[i–2^k+ 1] + … + A[i]
其中,k为i最末尾1之后零的个数。比如0d10的二进制是1010,则k=0b10
我们称C为树状数组。
当我们修改A[i]的值时,我们需要从C[i]往根节点一路上溯,调整这条路上的所有C[],这个操作的复杂度在最坏情况下就是树的高度即O(logn)。这个操作看起来有点麻烦,但是对于求数列的前n项和确实有不少好处:如同上面求C8的例子一样,只需要找到n=8以前的所有最大子树,把其根节点的C加起来即可。不难发现,这些子树的数目是n在二进制时1的个数,或者说是把n展开成2的幂方和时的项数,因此,求和操作的复杂度也是O(logn)。
(形式化)求任意区间的和:
求A[i] + A[i+1] + … + A[j],设sum(k) = A[1]+A[2]+…+A[k],则
A[i] + A[i+1] + … + A[j] = sum(j)-sum(i-1)。
知道了树状数组的好处,下面再来说一说C[i]的定义中的A[i-2^k+1]。简单一点解释吧(人家设计的太巧妙,看懂就行了= =):给定i,如何求2^k?
2^k=i&(i^(i-1)) , 或者i&(-i)
求k的java方法:
//求k
public int lowbit(int t){
return t&(t^(t-1));
}剩下的就是修改和求和操作了:
//修改数组元素
public void modyValue(int pos,int value){
while (pos<=arr_len) {//arr_len为数组C长度
C[pos]+=value;
pos+=lowbit(pos);
}
} //获得前n项和
public int calSum(int end){
int sum=0;
while (end>0) {
sum+=C[end];
end-=lowbit(end);
}
return sum;
}三.问题实例
题目来源
- 当在网上购物使用关键词搜索商品时,可以选择很多附选条件,比如品牌,价格等,之后会出现符合当前条件的商品及数量,例如搜索词为:羽绒服,附选条件为:价格¥500-¥1000
- 商品数量会因为商家上架、下架商品而改变,因此买家在不同时间段搜索商品时,显示的数量会不一样。
- 接下来包含一个含有多行的文本文件,文件的每行代表上架,下架,查询三种行为的一种,本题默认查询对象是‘衣服’。
请计算所有买家查询结果的总和。
- 举例: 一个拥有6行的文件。
- up 3 11 (有一个商家上架了3件11rmb的衣服。)
- query 11 25 (有一个买家查询11rmb-25rmb的衣服的数量。这里的查询结果是:3件)
- up 5 25 (有一个商家上架了5件25rmb的衣服。)
- query 11 25 (有一个买家查询11rmb-25rmb的衣服的数量。这里的查询结果是:8件)
- down 3 25 (有一个商家下架了3件25rmb的衣服。)
- query 20 25 (有一个买家查询20rmb-25rmb的衣服的数量。这里的查询结果是:2件)
这题的答案是所有买家查询结果的总和为13(3+8+2=13)。
当数据量为一千行,普通办法解决:
//建了一个长度为100000的Hash数组,
public class GoodsNum {
public static void main(String[] args) {
long startTime=System.currentTimeMillis();
int[] hash=new int[100000];//存储货物价格和数量的哈希数组
String pathname="files/myfile.txt";
try {
FileReader fr=new FileReader(new File(pathname));
BufferedReader br=new BufferedReader(fr);//按行读文件
String str="";
long sum=0;//结果和的初始化
while ((str=br.readLine())!=null) {
if(str.startsWith("up")){
hash[Integer.parseInt(str.split(" ")[2].trim())]+=Integer.parseInt(str.split(" ")[1].trim());
}
else if (str.startsWith("down")) {
if(hash[Integer.parseInt(str.split(" ")[2].trim())]==0){
System.out.println("operation error!");
continue;
}
hash[Integer.parseInt(str.split(" ")[2].trim())]-=Integer.parseInt(str.split(" ")[1].trim());
if(hash[Integer.parseInt(str.split(" ")[2].trim())]<0) hash[Integer.parseInt(str.split(" ")[2].trim())]=0;
}
else if (str.startsWith("query")){
int begin=Integer.parseInt(str.split(" ")[1]);
int end=Integer.parseInt(str.split(" ")[2]);
for(int i=begin;i<=end;i++){
if(hash[i]>0)
sum+=hash[i];
}
}
else {
System.out.println("wrong operation!---"+str);
break;
}
}
System.out.println(sum);
System.out.println((System.currentTimeMillis()-startTime)+"ms");
} catch (Exception e) {
e.printStackTrace();
}
}
}运行结果:

好吧,数据量来到了100000行,货物的价格也变大了。(其实并不是很大,那道五十亿行的问题还没想明白咋回事,看看效果)
普通版本运行结果:
长了不止一点点…然后是树状数组的版本,先上代码:
public class GoodsNum2 {
private int arr_len=99999;
private int []C=new int[arr_len+1];//数组C从1开始存,所以初始化加一
public static void main(String[] args) {
long startTime=System.currentTimeMillis();
String pathname="files/myfile2.txt";
FileReader fr;
GoodsNum2 ob=new GoodsNum2();
long sum=0;
try {
fr = new FileReader(new File(pathname));
BufferedReader br=new BufferedReader(fr);//按行读文件
String str="";
while ((str=br.readLine())!=null) {
String []result=str.split(" ");
int goodsNumOrPrice=Integer.parseInt(result[1]);
int goodsPrice=Integer.parseInt(result[2]);
if(str.startsWith("up")){
ob.modyValue(goodsPrice, goodsNumOrPrice);
}
else if (str.startsWith("down")) {
ob.modyValue(goodsPrice, (-goodsNumOrPrice));
}
else if (str.startsWith("query")){
sum+=ob.calSum(goodsPrice)-ob.calSum(goodsNumOrPrice-1);
}
else {
System.out.println("wrong operation!"+str);
break;
}
}
System.out.println("sum="+sum);
System.out.println((System.currentTimeMillis()-startTime)+"ms");
} catch (Exception e) {
e.printStackTrace();
}
}
public int lowbit(int t){
return t&(t^(t-1));
}
public void modyValue(int pos,int value){
while (pos<=arr_len) {
C[pos]+=value;
pos+=lowbit(pos);
}
}
public int calSum(int end){
int sum=0;
while (end>0) {
sum+=C[end];
end-=lowbit(end);
}
return sum;
}
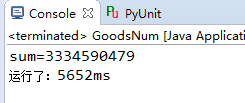
}结果:
这速度简直震撼啊!优秀的数据结构和算法就这给么给力!在这些东东面前,自己真是太尼玛渺小了。。。























 635
635

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








