求一段连续自然数的异或结果

背景

• 最近看到用异或找出连续自然数中某一值重复1次/缺失的问题（出现奇偶次不同作为查找特征的问题），针对其中与高斯求和法相类比的连续自然数(或连续整数)值求异或法，给出一种快速求法，最坏时间复杂度为7次异或。

1. 预定义

• 定义域：$N$
• 基本运算：异或符号记作$⨁$，真值表：
  
• 对应法则：记$f(a,b)={⨁}_{i=a}^{b}i=a⨁(a+1)⨁\dots ⨁b,a<b且a,b\in N$。
• 规定：异或是双目运算符，当$b=a$时，特别规定$f(a,b)=f(a,a)=a$，表示未参与异或运算。

2. 结论

$$f(a,b)=f(a-1-mod(a-1,4),a-1)⨁f(b-mod(b,4),b)，其中a,b\in N,a\le b$$
其中$mod$为取余运算。

• 代码示例：(示例代码的适用范围已从连续自然数扩展为连续整数，见推论1)

from _operator import xor, mod

# f(a,b) = f(a-1-mod(a-1,4),a-1)⨁f(b-mod(b,4),b)
def N_seq_xor(a, b):
    if not isinstance(a, int) or not isinstance(b, int):
        raise ValueError('Parameters should be integers!')
        
    if a > b:
        print('Warning: Parameters should be in ascending order! Try to exchange the values of "a" and "b" before running!')
        return N_seq_xor(b, a)
        
    pace = b - a
    if pace < 4:  # 0 won't make any difference to the xor result.
        a_0 = a
        a_1 = 0 if pace < 1 else a_0 + 1
        a_2 = 0 if pace < 2 else a_0 + 2
        a_3 = 0 if pace < 3 else a_0 + 3
        return xor(xor(a_0, a_1), xor(a_2, a_3))
    else:
        return xor(N_seq_xor(a-1-mod(a-1, 4), a-1), N_seq_xor(b-mod(b, 4), b))

推论
推论部分为3.证明之后的额外内容，可略过。

• 推论1：以$0$与除数$y$构成的半开区间为模除的值域（即$[0,y)$和$(-y,0]$，$y\in N^{+}$），补充$mod$定义
  $\begin{array}{rl}& mod(-x,y)=-mod(x,y)+y,\\ & mod(x,-y)=mod(x,y)-y,\\ & mod(-x,-y)=-mod(x,y),\end{array}其中x\in N,y\in N^{+}$，
  则公式
  $$f(a,b)=f(a-1-mod(a-1,4),a-1)⨁f(b-mod(b,4),b)，其中a,b\in Z,a\le b$$
  仍成立，且公式（1）（2）（3）仍成立（证明略）。
• 推论2：特别地，当$a=4k,k\in Z$且$b\in Z,a\le b$时，$mod(a,4)=0$,
  记$pace=mod(b-a,4)$，则有

$pace$	$f(a,b)$
$0$	$b$
$1$	$1$
$2$	$b+1$
$3$	$0$

• 代码示例：(示例代码的适用范围已从连续自然数扩展为连续整数，见推论1)

from _operator import xor, mod

def N_seq_xor_4k_start(a, b):
    if not isinstance(a, int) or not isinstance(b, int):
        raise ValueError('Parameters should be integers!')
        
    if a > b:
        raise ValueError('Parameters should be in ascending order!')
    
    if mod(a, 4) != 0:
        raise ValueError('Integer "a" must be a multiple of 4!')
    
    results = [b, 1, b + 1, 0]
    return results[mod(b, 4)]

if __name__ == "__main__":
    # print(N_seq_xor(0, 10))
    # print(N_seq_xor_4k_start(0, 10))

    a = -4
    b_list = range(a, 16)
    for b in b_list:
        # y = N_seq_xor(a, b)
        y = N_seq_xor_4k_start(a, b)
        print(a, b, y)
        if mod(b, 4) == 3:
            print()

推论2证明：
在推论1的补充定义下，当 $a=4k,k\in Z$且$a\le b$ 时，
有 $mod(b,4)=mod(b-4k,4)=mod(b-a,4)=pace,k\in Z$，
可记 $b=4k^{\prime }+mod(b,4)=4k^{\prime }+pace,k^{\prime }\in Z$；
由公式（1）$f(4k,4k+3)=0,k\in N$及推论1,
可得 $f(4(k-1),4(k-1)+3)=0,k\in Z$
故
$$\begin{array}{rl}f(a,b)& =f(a-1-mod(a-1,4),a-1)⨁f(b-mod(b,4),b)\\ & =f(4k-1-mod(4k-1,4),4k-1)⨁f(b-pace,b)\\ & =f(4k-1-mod(4k-1,4),4k-1)⨁f(4k^{\prime },4k^{\prime }+pace)\\ & =f(4k-1-3,4k-1)⨁f(4k^{\prime },4k^{\prime }+pace)\\ & =f(4(k-1),4(k-1)+3)⨁f(4k^{\prime },4k^{\prime }+pace)\\ & =0⨁f(4k^{\prime },4k^{\prime }+pace)\\ & =f(4k^{\prime },4k^{\prime }+pace)\end{array}$$
当 $pace=0$ 时，$b=4k^{\prime }+0$, $f(a,b)=f(4k^{\prime },4k^{\prime }+0)=f(b,b)=b$，
当 $pace=1$ 时，$b=4k^{\prime }+1$, $f(a,b)=f(4k^{\prime },4k^{\prime }+1)=1$，
当 $pace=2$ 时，$b=4k^{\prime }+2$, $f(a,b)=f(4k^{\prime },4k^{\prime }+2)=1⨁(4k^{\prime }+2)=4k^{\prime }+3=b+1$，
当 $pace=3$ 时，$b=4k^{\prime }+3$, $f(a,b)=f(4k^{\prime },4k^{\prime }+3)=(4k^{\prime }+3)⨁(4k^{\prime }+3)=0$。
得证。

3. 证明

3.1 异或性质：

• 1、交换律：$a⨁b=b⨁a$
• 2、结合律：$(a⨁b)⨁c=a⨁(b⨁c)$
• 3、基本等式：$a⨁a=0，a⨁0=a，a⨁b⨁b=a$
  其中$a,b,c\in N$
• 4、二进制分配率及推论：
  设序列 a 0 , a 1 , … , a m , b 0 , b 1 , … , b n ∈ { 0 , 1 } a_0,a_1,…,a_m,b_0,b_1,…,b_n∈\{0,1\} a0​,a1​,…,am​,b0​,b1​,…,bn​∈{0,1}，自然数$a=(a_m\dots a_1{a}_0{)}_2$，$b=(b_n\dots b_1{b}_0{)}_2$
  则$a⨁b=(a_m\dots a_1{a}_0{)}_2⨁(b_n\dots b_1{b}_0{)}_2$，当$m\ge n$时，有：
  $$\begin{gathered} a⨁b=(a_m\dots a_n\dots a_1{a}_0{)}_2⨁(b_n\dots b_1{b}_0{)}_2 \\ =[val(a_m⨁0)\dots val(a_{n+1}⨁0)val(a_n⨁b_n)\dots val(a_1⨁b_1)val(a_0⨁b_0){]}_2 \end{gathered}$$
  其中$val(a_n⨁b_n)$是$a_n⨁b_n$的值，将值赋给第$n$位。
  令$b_{n+1},b_{n+2}\dots ,b_m=0$则可简化为：
  $$a⨁b=[val(a_m⨁b_m)\dots val(a_1⨁b_1)val(a_0⨁b_0){]}_2$$
  转为十进制：
  $$\begin{gathered} a⨁b=[val(a_m⨁b_m)\dots val(a_1⨁b_1)val(a_0⨁b_0){]}_2 \\ =val(a_m⨁b_m)\ast 2^m+\cdots +val(a_1⨁b_1)\ast 2^1+val(a_0⨁b_0)\ast 2^0 \\ =\sum _{i=0}^{m}val(a_i⨁b_i)\ast 2^i \end{gathered}$$
  当$m<n$时同理有：$a⨁b={\sum }_{i=0}^{n}val(a_i⨁b_i)\ast 2^i$
  综上：
  $$a⨁b=\sum _{i=0}^{\max (m,n)}val(a_i⨁b_i)\ast 2^i$$
  以十进制自然数$x$为例，其转二进制公式为：
  $$\begin{gathered} x=\sum _{i=0}^{k}mo{d}_{i+1}(x,2)\ast 2^i \\ =[mo{d}_{k+1}(x,2)\dots mo{d}_2(x,2)mo{d}_1(x,2){]}_2 \end{gathered}$$
  其中$k=\lfloor lo{g}_{2}x\rfloor ,mo{d}_{i+1}(x,2)$表示 $x$除$2$取余数运算第$i+1$次的结果，即$x$的二进制表示中相应位的值，$2^i$则是相应位的进率。
  $$\begin{gathered} a⨁b=(\sum _{i=0}^{k_a}mo{d}_{i+1}(a,2)\ast 2^i)⨁(\sum _{i=0}^{k_b}mo{d}_{i+1}(b,2)\ast 2^i) \\ =[mo{d}_{k_a+1}(a,2)\dots mo{d}_2(a,2)mo{d}_1(a,2){]}_2⨁[mo{d}_{k_b+1}(b,2)\dots mo{d}_2(b,2)mo{d}_1(b,2){]}_2 \\ =\sum _{i=0}^{\max (k_a,k_b)}val[mo{d}_{i+1}(a,2)⨁mo{d}_{i+1}(b,2)]\ast 2^i \end{gathered}$$
  其中$k_a=\lfloor lo{g}_{2}a\rfloor ,k_b=\lfloor lo{g}_{2}b\rfloor$。

3.2 连续自然数的异或

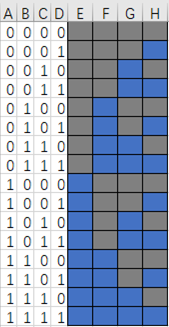
异或可看作统计二进制表示中对应位状态为1的奇偶个数的运算。从图中看出如下规律：
$$f(4k,4k+3)=0,k\in N\text{\hspace{1em}(1)}$$
显然（数学归纳法）推论为
$$f(4k_1,4k_2+3)=0,k_1,k_2\in N且k_1\le k_2$$
于是有
$$\begin{gathered} f(0,b)=f(0,b-mod(b,4)-1)⨁f(b-mod(b,4),b) \\ =0⨁f(b-mod(b,4),b) \\ =f(b-mod(b,4),b) \end{gathered}$$
其中$b\in N且b\ge 4$。注意自然数$b-mod(b,4)$是$4$的倍数，即 b − m o d ( b , 4 ) ∈ { x ∣ x = 4 k , k ∈ N } b-mod(b,4)∈\{x|x=4k,k∈N\} b−mod(b,4)∈{x∣x=4k,k∈N}。
当$b\in [0,3]$时，可得$b-mod(b,4)=0$：而$f(0,b)=f(b-mod(b,4),b)$仍然成立。
综上：
$$f(0,b)=f(b-mod(b,4),b),b\in N$$
最终求出
$$\begin{gathered} f(a,b)=f(0,a-1)⨁f(0,a-1)⨁f(a,b) \\ =f(0,a-1)⨁f(0,b) \\ =f(a-1-mod(a-1,4),a-1)⨁f(b-mod(b,4),b) \end{gathered}$$
最坏时间复杂度为7次异或。

---

注意事项：
$f(4k,4k-3)$中的$4k$是$4$的倍数，此函数本身并不是周期函数，而是在震荡特性上类似于函数$y=xsin(\pi /2\ast x)$，只是存在一个特殊的周期序列。
本文到此已基本结束，有兴趣的可以继续看下文的证明，仅作参考，如有错误恳请指正。

---

附：
证$（1）$：
当$k=0$时：
$$\begin{gathered} f(4k,4k-3)=f(0,3) \\ =0⨁1⨁2⨁3 \\ =(00{)}_2⨁(01{)}_2⨁(10{)}_2⨁(11{)}_2 \\ =(00{)}_2=0 \end{gathered}$$
当$k\in N^{+}$时：
$$\begin{gathered} f(4k,4k-3)=4k⨁(4k+1)⨁(4k+2)⨁(4k+3) \\ =\sum _{i=0}^{\lfloor lo{g}_2(4k+3)\rfloor }val[mo{d}_{i+1}(4k,2)⨁mo{d}_{i+1}(4k+1,2)⨁mo{d}_{i+1}(4k+2,2)⨁mo{d}_{i+1}(4k+3,2)]\ast 2^i \\ =\sum _{i=2}^{\lfloor lo{g}_2(4k+3)\rfloor }val[mo{d}_{i+1}(4k,2)⨁mo{d}_{i+1}(4k+1,2)⨁mo{d}_{i+1}(4k+2,2)⨁mo{d}_{i+1}(4k+3,2)]\ast 2^i \\ +val[mo{d}_2(4k,2)⨁mo{d}_2(4k+1,2)⨁mo{d}_2(4k+2,2)⨁mo{d}_2(4k+3,2)]\ast 2^1 \\ +val[mo{d}_1(4k,2)⨁mo{d}_1(4k+1,2)⨁mo{d}_1(4k+2,2)⨁mo{d}_1(4k+3,2)]\ast 2^0 \end{gathered}$$
当$i=0$时：
$$mo{d}_1(4k,2)⨁mo{d}_1(4k+1,2)⨁mo{d}_1(4k+2,2)⨁mo{d}_1(4k+3,2)=0⨁1⨁0⨁1=0$$
当$i=1$时：
$$mo{d}_2(4k,2)⨁mo{d}_2(4k+1,2)⨁mo{d}_2(4k+2,2)⨁mo{d}_2(4k+3,2)=0⨁0⨁1⨁1=0$$
当$i\ge 2$时（证明附后）：
$$\lfloor lo{g}_{2}4k\rfloor =\lfloor lo{g}_2(4k+1)\rfloor =\lfloor lo{g}_2(4k+2)\rfloor =\lfloor lo{g}_2(4k+3)\rfloor ,k\in N^{+}\text{\hspace{1em}(2)}$$
$$\begin{gathered} mo{d}_{i+1}(4k,2)=mo{d}_{i+1}(4k+1,2)=mo{d}_{i+1}(4k+2,2)=mo{d}_{i+1}(4k+3,2), \\ k\in N^{+},i\ge 2\text{\hspace{1em}(3)} \end{gathered}$$
故：
f ( 4 k , 4 k − 3 ) = { ∑ i = 2 ⌊ l o g 2 ⁡ ( 4 k + 3 ) ⌋ v a l [ m o d i + 1 ( 4 k , 2 ) ⨁ m o d i + 1 ( 4 k + 1 , 2 ) ⨁ m o d i + 1 ( 4 k + 2 , 2 ) ⨁ m o d i + 1 ( 4 k + 3 , 2 ) ] ∗ 2 i } + v a l [ 0 ⨁ 0 ⨁ 1 ⨁ 1 ] ∗ 2 1 + v a l [ 0 ⨁ 1 ⨁ 0 ⨁ 1 ] ∗ 2 0 = { ∑ i = 2 ⌊ l o g 2 ⁡ ( 4 k + 3 ) ⌋ v a l [ m o d i + 1 ( 4 k , 2 ) ⨁ m o d i + 1 ( 4 k , 2 ) ⨁ m o d i + 1 ( 4 k , 2 ) ⨁ m o d i + 1 ( 4 k , 2 ) ] ∗ 2 i } + v a l [ 0 ⨁ 0 ⨁ 1 ⨁ 1 ] ∗ 2 1 + v a l [ 0 ⨁ 1 ⨁ 0 ⨁ 1 ] ∗ 2 0 = [ ∑ i = 2 ⌊ l o g 2 ⁡ ( 4 k + 3 ) ⌋ 0 ∗ 2 i ] + 0 ∗ 2 1 + 0 ∗ 2 0 = 0 \begin{aligned} f(4k,4k-3)&=\{∑_{i=2}^{⌊log_2⁡ (4k+3)⌋} val[mod_{i+1} (4k,2)⨁mod_{i+1} (4k+1,2)⨁mod_{i+1} (4k+2,2)⨁mod_{i+1} (4k+3,2)]*2^i \} + \\ &val[0⨁0⨁1⨁1]*2^1+ val[0⨁1⨁0⨁1]*2^0 \\ &=\{∑_{i=2}^{⌊log_2⁡ (4k+3)⌋} val[mod_{i+1} (4k,2)⨁mod_{i+1} (4k,2)⨁mod_{i+1} (4k,2)⨁mod_{i+1} (4k,2)]*2^i \} + \\ &val[0⨁0⨁1⨁1]*2^1+ val[0⨁1⨁0⨁1]*2^0 \\ &=[∑_{i=2}^{⌊log_2⁡ (4k+3) ⌋} 0*2^i]+0*2^1+0*2^0 \\ &=0 \end{aligned} f(4k,4k−3)​={i=2∑⌊log2​⁡(4k+3)⌋​val[modi+1​(4k,2)⨁modi+1​(4k+1,2)⨁modi+1​(4k+2,2)⨁modi+1​(4k+3,2)]∗2i}+val[0⨁0⨁1⨁1]∗21+val[0⨁1⨁0⨁1]∗20={i=2∑⌊log2​⁡(4k+3)⌋​val[modi+1​(4k,2)⨁modi+1​(4k,2)⨁modi+1​(4k,2)⨁modi+1​(4k,2)]∗2i}+val[0⨁0⨁1⨁1]∗21+val[0⨁1⨁0⨁1]∗20=[i=2∑⌊log2​⁡(4k+3)⌋​0∗2i]+0∗21+0∗20=0​
综上：$$f(4k,4k-3)=0,k\in N$$
证毕。

证$（2）$：
$$\begin{gathered} k\in N^{+} \\ \lfloor lo{g}_{2}k\rfloor ,\lfloor lo{g}_{2}k\rfloor +1\in N \\ {2}^{\lfloor lo{g}_{2}k\rfloor },2^{\lfloor lo{g}_{2}k\rfloor +1}\in N \end{gathered}$$
根据下取整定义:
$$\begin{gathered} \lfloor lo{g}_{2}k\rfloor \le lo{g}_{2}k<\lfloor lo{g}_{2}k\rfloor +1 \\ {2}^{\lfloor lo{g}_{2}k\rfloor }\le k<2^{\lfloor lo{g}_{2}k\rfloor +1} \end{gathered}$$
又$k,2^{\lfloor lo{g}_{2}k\rfloor +1}\in N$：
$$2^{\lfloor lo{g}_{2}k\rfloor }\le k<k+1\le 2^{\lfloor lo{g}_{2}k\rfloor +1}$$
故有：
$$\begin{gathered} 2^{\lfloor lo{g}_{2}k\rfloor }\le k<k+\frac{3}{4}<k+1\le 2^{\lfloor lo{g}_{2}k\rfloor +1} \\ \lfloor lo{g}_{2}k\rfloor \le lo{g}_{2}k<lo{g}_2(k+\frac{3}{4})<lo{g}_2(k+1)\le \lfloor lo{g}_{2}k\rfloor +1 \end{gathered}$$
即有
$$\lfloor lo{g}_{2}k\rfloor <lo{g}_2(k+\frac{3}{4})<\lfloor lo{g}_{2}k\rfloor +1$$
根据下取整的定义、单调不减性质可得:
$$\lfloor lo{g}_{2}k\rfloor \le \lfloor lo{g}_2(k+\frac{3}{4})\rfloor \le lo{g}_2(k+\frac{3}{4})<\lfloor lo{g}_{2}k\rfloor +1$$
又由于$\lfloor lo{g}_{2}k\rfloor ,\lfloor lo{g}_2(k+\frac{3}{4})\rfloor \in N$，故可根据上式中$\lfloor lo{g}_2(k+\frac{3}{4})\rfloor <\lfloor lo{g}_{2}k\rfloor +1$得
$$\lfloor lo{g}_2(k+\frac{3}{4})\rfloor \le (\lfloor lo{g}_{2}k\rfloor +1)-1=\lfloor lo{g}_{2}k\rfloor$$
综合以上两个不等式，得
$$\lfloor lo{g}_{2}k\rfloor \le \lfloor lo{g}_2(k+\frac{3}{4})\rfloor \le \lfloor lo{g}_{2}k\rfloor$$
根据下取整的定义、单调不减性质，得
$$\lfloor lo{g}_{2}k\rfloor \le \lfloor lo{g}_2(k+\frac{1}{4})\rfloor \le \lfloor lo{g}_2(k+\frac{2}{4})\rfloor \le \lfloor lo{g}_2(k+\frac{3}{4})\rfloor \le \lfloor lo{g}_{2}k\rfloor$$
故
$$\lfloor lo{g}_{2}k\rfloor =\lfloor lo{g}_2(k+\frac{1}{4})\rfloor =\lfloor lo{g}_2(k+\frac{2}{4})\rfloor =\lfloor lo{g}_2(k+\frac{3}{4})\rfloor$$
而
$$\begin{gathered} \lfloor lo{g}_2(4k+3)\rfloor =\lfloor lo{g}_{2}4(k+\frac{3}{4})\rfloor =\lfloor 2+lo{g}_2(k+\frac{3}{4})\rfloor =2+\lfloor lo{g}_2(k+\frac{3}{4})\rfloor \\ =2+\lfloor lo{g}_{2}k\rfloor =\lfloor 2+lo{g}_{2}k\rfloor =\lfloor lo{g}_{2}4k\rfloor \end{gathered}$$
同理可证：
$$\begin{gathered} \lfloor lo{g}_2(4k+2)\rfloor =\lfloor lo{g}_{2}4k\rfloor \\ \lfloor lo{g}_2(4k+1)\rfloor =\lfloor lo{g}_{2}4k\rfloor \end{gathered}$$
故
$$\lfloor lo{g}_{2}4k\rfloor =\lfloor lo{g}_2(4k+1)\rfloor =\lfloor lo{g}_2(4k+2)\rfloor =\lfloor lo{g}_2(4k+3)\rfloor ,k\in N^{+}$$
证毕。

证$（3）$：
已知$k\in N^{+},i\ge 2$。
将$4k$用二进制展开：
$$4k=[mo{d}_{\lfloor lo{g}_{2}4k\rfloor +1}(4k,2)\dots mo{d}_3(4k,2)00{]}_2$$
则有：
$$\begin{array}{rl}4k+1& =[mo{d}_{\lfloor lo{g}_{2}4k\rfloor +1}(4k,2)\dots mo{d}_3(4k,2)00{]}_2+1\\ & =[mo{d}_{\lfloor lo{g}_{2}4k\rfloor +1}(4k,2)\dots mo{d}_3(4k,2)00{]}_2+[01{]}_2\\ & =[mo{d}_{\lfloor lo{g}_{2}4k\rfloor +1}(4k,2)\dots mo{d}_3(4k,2)01{]}_2\end{array}$$
注意最后的等号是恒等变形，未对前面的位有任何改动。
另一方面，将$4k+1$用二进制展开：
$$4k+1=[mo{d}_{\lfloor lo{g}_2(4k+1)\rfloor +1}(4k+1,2)\dots mo{d}_3(4k+1,2)01{]}_2$$
又由于$（2）$中已证明
$$\lfloor lo{g}_{2}4k\rfloor =\lfloor lo{g}_2(4k+1)\rfloor =\lfloor lo{g}_2(4k+2)\rfloor =\lfloor lo{g}_2(4k+3)\rfloor$$
得
$$4k+1=[mo{d}_{\lfloor lo{g}_{2}4k\rfloor +1}(4k+1,2)\dots mo{d}_3(4k+1,2)01{]}_2$$
即
$$\begin{gathered} [mo{d}_{\lfloor lo{g}_{2}4k\rfloor +1}(4k,2)\dots mo{d}_3(4k,2)01{]}_2 \\ =[mo{d}_{\lfloor lo{g}_{2}4k\rfloor +1}(4k+1,2)\dots mo{d}_3(4k+1,2)01{]}_2 \end{gathered}$$
于是有
$$mo{d}_{i+1}(4k,2)=mo{d}_{i+1}(4k+1,2)$$
同理可证：
$$\begin{gathered} mo{d}_{i+1}(4k,2)=mo{d}_{i+1}(4k+2,2) \\ mo{d}_{i+1}(4k,2)=mo{d}_{i+1}(4k+3,2) \end{gathered}$$
综上：
$$\begin{gathered} mo{d}_{i+1}(4k,2)=mo{d}_{i+1}(4k+1,2)=mo{d}_{i+1}(4k+2,2)=mo{d}_{i+1}(4k+3,2), \\ k\in N^{+},i\ge 2 \end{gathered}$$
证毕。