斐波那契数列及青蛙跳台阶问题

1、考察知识点：递归与循环

2、题目一：写一个函数，输入n，求斐波那契数列的第n项。斐波那契数列的定义如下：

• 
• 
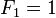
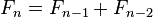• (n≧2)

3、递归解法：

long long Fibonacci(unsigned int n)
{
    if(n<=0)
        return 0;
    if(n == 1)
        return 1;
    return Fibonacci(n-1)+Fibonacci(n-2);

}

缺点：该递归解法会重复计算很多结点，效率低下，时间复杂度是以n的指数方式递增的。

4、非递归解法(循环)

long long Fibonacci(unsigned int n)
{
   int result[2]={0,1};
   if(n<2)
      return result[n];
   long long one=1;
   long long two=0;
   long long fib=0;
   for(int i=2;i<=n;i++)
   {
      fib=one+two;
      two=one;
      one=fib;
    } 
    return fib;
}

该非递归解法的时间复杂度为O(n)

5、时间复杂度为O(logn)但不实用的解法

该解法巧妙的利用了一个数学公式：

我们只需要求得等式右边即可得到f(n)。至于具体编程求解在这里不再详叙，有兴趣童靴可以自己去找。

6、题目二：(斐波那契数列数列的应用建模)

一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级的台阶共有多少中跳法。

解题思路：我们把n级台阶的跳法看成是n的函数，记为f(n)。当n>2时，第一次跳的时候就有两种不同的选择：一是第一次只跳1级，此时跳法数目等于后面剩下的n-1级台阶的跳法数目，即为f(n-1)；另外一种选择是第一次跳2级，此时跳法数目等于后面剩下的n-2级台阶的跳法数目，即为f(n-2)。因此n级台阶的不同跳法的总数f(n)=f(n-1)+f(n-2)。这实际上就是一个斐波那契数列。

题目扩展：如果把条件改成：一只青蛙一次可以跳上1级台阶，也可以跳上2级....也可以跳上n级，此时该青蛙跳上一个n级的台阶总共有多少种的跳法？

问题分析：

用Fib(n)表示青蛙跳上n阶台阶的跳法数，青蛙一次性跳上n阶台阶的跳法数为1（n阶跳），设定Fib(0)=1；

当n=1时，只有一种跳法，即1阶跳，Fib(1)=1；

当n=2时，有两种跳法，一阶跳和二阶跳：Fib(2)=Fib(1)+Fib(0)=2;

当n=3时，有三种跳法，第一次跳出一阶后，后面还有Fib(n-1)种跳法；第一次跳出二阶后，后面还有Fib(n-2)种跳法；第一次跳出3阶后，后面还有Fib(n-n)重跳法；

Fib(3)=Fib(2)+Fib(1)+Fib(0)=4；

所以，当n=n时，共有n种跳的方式，Fib(n)=Fib(n-1)+Fib(n-2)+Fib(n-3)+...+Fib(n-n)=Fib(0)+Fib(1)+Fib(2)+....+Fib(n-1)

求得：Fib(n)=2*Fib(n-1)  (n>=2)

所以递归等式如下：