hdu 4486 Pen Counts

最新推荐文章于 2021-02-27 11:50:39 发布

疯狂的橡树

最新推荐文章于 2021-02-27 11:50:39 发布

阅读量1.5k

点赞数

分类专栏：模拟文章标签： ACM c 算法

本文链接：https://blog.csdn.net/bossup/article/details/9929719

版权

模拟专栏收录该内容

2 篇文章 0 订阅

订阅专栏

Pen Counts

Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 246 Accepted Submission(s): 144

Problem Description

Chicken farmer Xiaoyan is getting three new chickens, Lucy, Charlie and CC. She wants to build a chicken pen so that each chicken has its own, unobstructed view of the countryside. The pen will have three straight sides; this will give each chicken its own side so it can pace back and forth without interfering with the other chickens. Xiaoyan finds a roll of chicken wire (fencing) in the barn that is exactly N feet long. She wants to figure out how many different ways she can make a three sided chicken pen such that each side is an integral number of feet, and she uses the entire roll of fence.
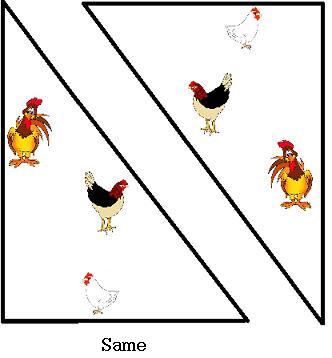
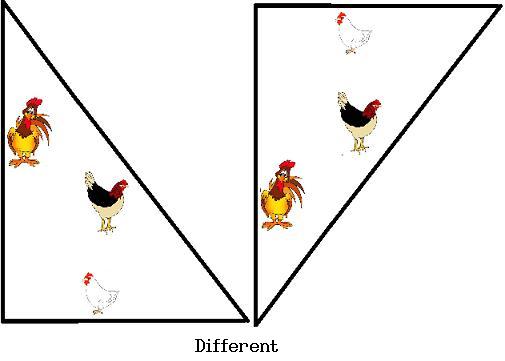
Different rotations of the same pen are the same, however, reflections of a pen may be different (see below).

Input

The first line of input contains a single integer P,(1<= P <=1000), which is the number of data sets that follow. Each data set should be processed identically and independently.

Each data set consists of a single line of input. It contains the data set number, K, and the length of the roll of fence, N, (3 <= N <= 10000).

Output

For each data set there is a single line of output. It contains the data set number, K, followed by a single space which is then followed by an integer which is the total number of different three-sided chicken pen configurations that can be made using the entire roll of fence.

Sample Input

Sample Output

Source

Greater New York 2012

Recommend

liuyiding

这题考的是三角形的一些知识。

题意：

给你三角形的周长。问你能构成多少边为整数的三角形。如果一个三角形能通过另一个三角形绕某一顶点得到的话那么这两个三角形算一个。

思路：

先总结一下三角形的相关知识。

设三角形周长为len。三边关系为l3>=l2>=l1。

两边之和>第三边。

所以三角形中最长边的取值范围为

len/3向上取整<=l3<len/2向上取整。

rest=len-l3。那么第二大边取值范围为

rest/2向下取整<l2<=l3。

对于一个等腰三角形其底边长的最大值<(len+1)/2。所以给定一个周长可以确定有多少个等腰或等边三角形。

所以每确定一个最长边那么三角形的个数是能确定的。

详细见代码：

#include <iostream>
#include<stdio.h>
using namespace std;

int main()
{
    int len,rest,l3,durl2,p,cas,ans;

    scanf("%d",&p);
    while(p--)
    {
        scanf("%d%d",&cas,&len);
        ans=0;
        for(l3=(len+2)/3;l3<(len+1)/2;l3++)//枚举最长边的长度
        {
            rest=len-l3;//剩下的的长度
            durl2=l3-(rest-1)/2;//第二大边的取值区间
            ans+=2*durl2;//三边都不同算两个
            if(!(rest&1))//可组成等腰三角形
                ans-=1;
            ans-=1;
        }
        if(len%3==0)//可组成等边
            ans+=1;
        printf("%d %d\n",cas,ans);
    }
    return 0;
}