二叉树的顺序存储及其Java实现

顺序存储充分利用满二叉树的特性，即每层的节点数分别为1、2、4、8。。。2ⁱ⁺¹，一个深度为i的二叉树最多只能包含2ⁱ-1个节点，因此只要定义一个长度为2ⁱ-1的数组即可存储这颗二叉树。

 

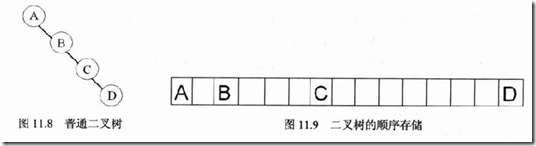
对于普通的不是满二叉树的，那些空出来的节点对应的数组元素留空即可，因此顺序存储会造成一定的空间浪费。如下图。

显然，如果是完全二叉树，那么就不会有空间浪费的情况；若是只有右子树，那么会造成相当大的浪费。

 

Java实现代码：

 

package com.liuhao.DataStructures;

import java.util.Arrays;

public class ArrayBinTree<T> {

	// 使用数组来记录所有节点
	private Object[] datas;
	private final int DEFAULT_DEEP = 8;
	// 保存该树的深度
	private int deep;
	// 数组的长度
	private int arraySize;

	// 以默认深度创建二叉树
	public ArrayBinTree() {
		this.deep = DEFAULT_DEEP;
		this.arraySize = (int) Math.pow(2, deep);
		datas = new Object[arraySize];
	}

	// 以指定深度创建
	public ArrayBinTree(int deep) {
		this.deep = deep;
		this.arraySize = (int) Math.pow(2, deep);
		datas = new Object[arraySize];
	}

	// 以指定深度，指定根节点创建
	public ArrayBinTree(int deep, T data) {
		this.deep = deep;
		this.arraySize = (int) Math.pow(2, deep);
		datas = new Object[arraySize];
		datas[0] = data;
	}

	/**
	 * 为指定节点添加子节点
	 * 
	 * @param index
	 *            需要添加子节点的父节点索引
	 * @param data
	 *            新的子节点的数据
	 * @param left
	 *            是否为左节点
	 */
	public void add(int index, T data, boolean left) {
		if (datas[index] == null) {
			throw new RuntimeException(index + "处节点为空，无法添加子节点！");
		}

		if (2 * index + 1 > arraySize || 2 * index + 2 > arraySize) {
			throw new RuntimeException("树底层数组已满");
		}

		if (left) {
			if (datas[2 * index + 1] == null) {
				datas[2 * index + 1] = data;
			} else {
				throw new RuntimeException("该节点已存在！");
			}
		} else {
			if (datas[2 * index + 2] == null) {
				datas[2 * index + 2] = data;
			} else {
				throw new RuntimeException("该节点已存在！");
			}
		}
	}

	// 判断二叉树是否为空
	public boolean isEmpty() {
		return datas[0] == null;
	}

	// 获取根节点
	public T getRoot() {
		return (T) datas[0];
	}

	// 返回指定节点的父节点
	public T getParent(int index) {
		if (index == 0) {
			throw new RuntimeException("根节点不存在父节点！");
		}

		return (T) datas[(index - 1) / 2];
	}
	
	//获取右子节点
	public T getRight(int index){
		if (2 * index + 1 > arraySize || 2 * index + 2 > arraySize) {
			throw new RuntimeException("该节点不存在右子节点！");
		}
		
		return (T) datas[index * 2 + 2];
	}
	
	//获取左子节点
	public T getLeft(int index){
		if (2 * index + 1 > arraySize || 2 * index + 2 > arraySize) {
			throw new RuntimeException("该节点不存在左子节点！");
		}
		
		return (T) datas[index * 2 + 1];
	}
	
	//返回该二叉树的深度
	public int getDeep(){
		return deep;
	}
	
	//返回指定数据的位置
	public int getPos(T data){
		for(int i=0;i<arraySize;i++){
			if(datas[i].equals(data)){
				return i;
			}
		}
		
		return -1;
	}
	
	public String toString(){
		return Arrays.toString(datas);
	}

}

从上面的介绍可以看出，顺序存储的思想就是将数中不同的节点存入数组的不同位置。比如，根节点，永远使用数组的第一个元素来保存；第二层的第二个节点，永远使用数组的第三个元素来保存。。。以此类推。

 

对于顺序存储的二叉树，不管是遍历还是查找，都可以有非常高的效率，唯一的缺点是空间浪费很大。

 

测试代码：

package com.liuhao.test;

import org.junit.Test;

import com.liuhao.DataStructures.ArrayBinTree;

public class ArrayBinTreeTest {

	@Test
	public void test() {
		ArrayBinTree<String> binTree = new ArrayBinTree<String>(4,"根");
		binTree.add(0, "0右", false);
		binTree.add(2, "2右", false);
		binTree.add(2, "2左", true);
		
		binTree.add(0, "0左", true);
		binTree.add(1, "1左", true);
		System.out.println(binTree);
		
		System.out.println(binTree.getLeft(2));
		System.out.println(binTree.getParent(6));
	}

}

---

您的关注是我坚持写作的动力，如果觉得有用，欢迎关注我的微信，海量学习资源免费送！