排序算法总结之堆排序

最新推荐文章于 2024-10-07 16:35:31 发布

hoxis

最新推荐文章于 2024-10-07 16:35:31 发布

阅读量1.5k

点赞数 1

分类专栏：笔试面试 Java进阶数据结构与算法分析文章标签：堆排序排序算法 java

本文链接：https://blog.csdn.net/bruce_6/article/details/38704301

版权

笔试面试同时被 3 个专栏收录

41 篇文章 4 订阅

订阅专栏

Java进阶

38 篇文章 4 订阅

订阅专栏

数据结构与算法分析

37 篇文章 3 订阅

订阅专栏

堆的概念。

n个关键字序列K_l，K₂，…，K_n称为堆，当且仅当该序列满足如下性质(简称为堆性质)：
(1) k_i≤K_2i且k_i≤K_2i+1 或(2)K_i≥K_2i且k_i≥K_2i+1(1≤i≤ )

满足（1）的称为小根堆，满足（2）的称为大根堆。
若将此序列所存储的向量R[1..n]看做是一棵完全二叉树的存储结构，则堆实质上是满足如下性质的完全二叉树：树中任一非叶结点的关键字均不大于(或不小于)其左右孩子(若存在)结点的关键字。

可以发现，大顶堆的根节点一定是这组数据中值最大的节点，也就是说，如果要对一组数据进行排序，只需先将这组建成大顶堆，就选出了其中的最大值。

堆排序

思想：

利用大顶堆(小顶堆)堆顶记录的是最大关键字(最小关键字)这一特性，使得每次从无序中选择最大记录(最小记录)变得简单。

堆排序的关键在于建堆，要按如下步骤完成(大顶堆)：

1)将初始待排序关键字序列(R1,R2....Rn)构建成大顶堆，此堆为初始的无序区；

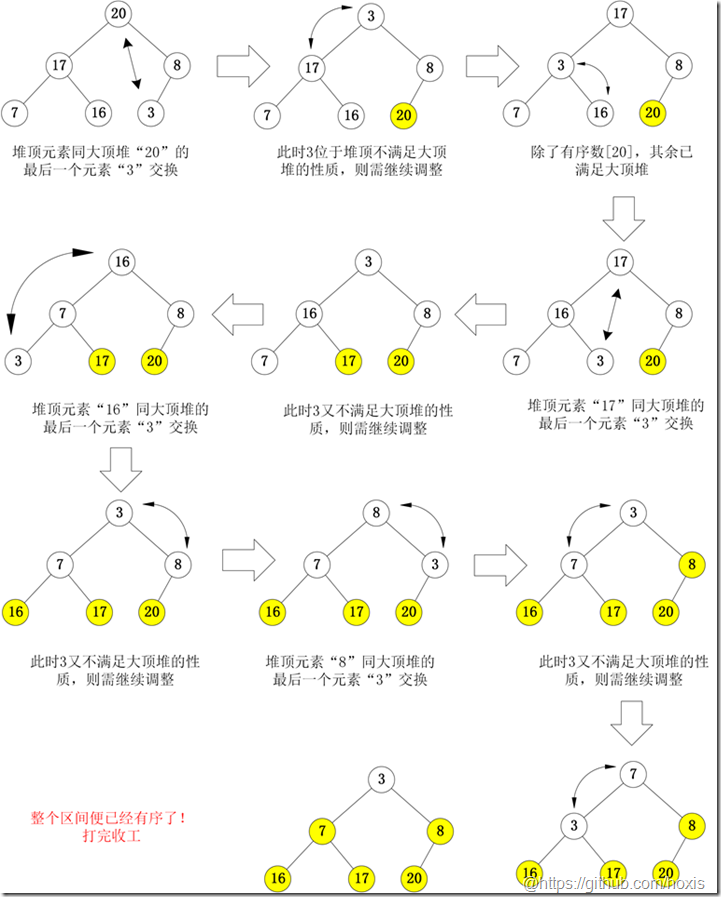
2)将堆顶元素R[1]与最后一个元素R[n]交换，此时得到新的无序区(R1,R2,......Rn-1)和新的有序区(Rn),且满足R[1,2...n-1]<=R[n];

3)由于交换后新的堆顶R[1]可能违反堆的性质，因此需要对当前无序区(R1,R2,......Rn-1)调整为新堆，然后再次将R[1]与无序区最后一个元素交换，得到新的无序区(R1,R2....Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为n-1，则整个排序过程完成。

排序过程

通过上面的介绍可以发现，堆排序的操作过程就是重复执行一下2步：

1)初始化堆：将R[1..n]构造为堆；

2)将当前无序区的堆顶元素R[1]同该区间的最后一个记录交换，然后将新的无序区调整为新的堆。

因此对于堆排序，最重要的两个操作就是构造初始堆和调整堆，其实构造初始堆事实上也是调整堆的过程，只不过构造初始堆是对所有的非叶节点都进行调整。

建堆（初始化堆）

下面举例说明：

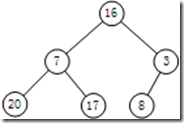
给定一个整形数组a[]={16,7,3,20,17,8}，对其进行堆排序。

首先根据该数组元素构建一个完全二叉树，得到

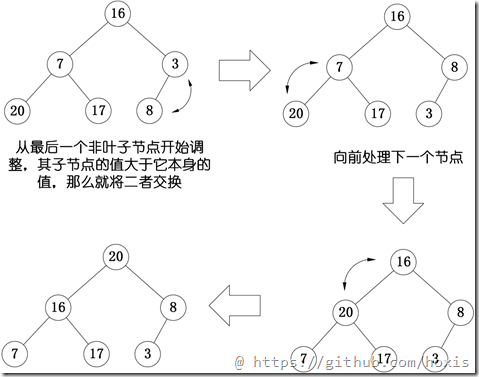
然后需要构造初始堆，则从最后一个非叶节点开始调整，每次调整都是从父节点、左孩子节点、右孩子节点三者中选择最大者跟父节点进行交换（交换之后可能造成被交换的孩子节点不满足堆的性质，因此每次交换之后要重新对被交换的孩子节点进行调整）。具体调整过程如下：

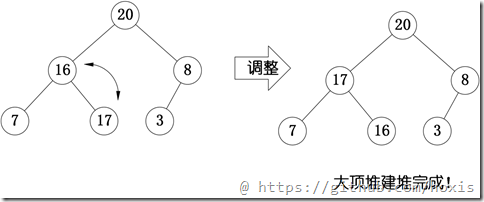
20和16交换后导致16不满足堆的性质，因此需重新调整

这样就得到了初始堆。

堆排序

将当前无序区的堆顶元素R[1]同该区间的最后一个记录交换，然后将新的无序区调整为新的堆。

从上述过程可知，堆排序其实也是一种选择排序，是一种树形选择排序。只不过直接选择排序中，为了从R[1...n]中选择最大记录，需比较n-1次，然后从R[1...n-2]中选择最大记录需比较n-2次。事实上这n-2次比较中有很多已经在前面的n-1次比较中已经做过，而树形选择排序恰好利用树形的特点保存了部分前面的比较结果，因此可以减少比较次数。对于n个关键字序列，最坏情况下每个节点需比较log2(n)次，因此其最坏情况下时间复杂度为 nlogn。堆排序为不稳定排序，不适合记录较少的排序。

Java实现

package com.liuhao.sort;

import java.util.Arrays;

public class HeapSort {
	public static void heapSort(DataWrap[] data) {
		System.out.println("开始排序");
		int arrayLen = data.length;

		// 循环建堆
		for (int i = 0; i < arrayLen - 1; i++) {
			// 建堆
			buildMaxHeap(data, arrayLen - 1 - i);
			// 交换堆顶元素和大顶堆的最后一个元素
			swap(data, 0, arrayLen - 1 - i);
			System.out.println(Arrays.toString(data));
		}
	}

	/**
	 * 对data数组从0到lastIndex建大顶堆
	 * 
	 * @param data
	 * @param lastIndex
	 */
	private static void buildMaxHeap(DataWrap[] data, int lastIndex) {

		// 从lastIndex处节点（最后一个节点）的父节点开始
		for (int i = (lastIndex - 1) / 2; i >= 0; i--) {
			int k = i; // 保存当前正在判断的节点

			// 如果当前k节点的子节点存在
			while (k * 2 + 1 <= lastIndex) {
				int biggerIndex = 2 * k + 1; // k节点的左子节点的索引

				// 如果biggerIndex < lastIndex，代表k节点存在右子节点，
				//那就先比较左、右节点的值大小，并将大者索引放在biggerIndex
				if (biggerIndex < lastIndex) {
					if (data[biggerIndex].compareTo(data[biggerIndex + 1]) < 0) {
						biggerIndex++;// biggerIndex总是代表较大子节点的索引
					}
				}

				// k节点处的值小于其子节点的值
				if (data[k].compareTo(data[biggerIndex]) < 0) {
					swap(data, k, biggerIndex);

					// 重新保证k节点的值大于其子节点的值，主要用于保证交换后k的子节点也满足大顶堆
					k = biggerIndex;
				} else {
					break;
				}
			}
		}
	}

	/**
	 * 交换data数组i、j索引处的元素
	 * 
	 * @param data
	 * @param i
	 * @param j
	 */
	private static void swap(DataWrap[] data, int i, int j) {
		DataWrap tmp = data[i];
		data[i] = data[j];
		data[j] = tmp;
	}

	public static void main(String[] args) {
		DataWrap[] data = { 
				new DataWrap(21, "")
				,new DataWrap(30, "")
				,new DataWrap(49, "")
				,new DataWrap(30, "*")
				,new DataWrap(16, "")
				,new DataWrap(9, "") };

		System.out.println("排序之前：" + Arrays.toString(data));

		heapSort(data);

		System.out.println("排序之后：" + Arrays.toString(data));
	}
}

排序效果：