第四单元用python学习微积分（二十七）积分-部分分式-分部积分

本文链接：https://blog.csdn.net/bullseye/article/details/124522174

本文介绍了使用Python进行微积分计算的方法，包括多项式的部分分式分解和分部积分。通过长除法和因式分解处理多项式，然后建立等式求解未知数。利用Sympy库计算复杂积分表达式，并展示了如何应用分部积分公式解决相关问题。此外，还探讨了积分的换算公式和圆盘法、壳层法求解立体体积。文章通过实际代码示例展示了如何利用Python进行数学计算和图形绘制。

摘要由CSDN通过智能技术生成

本文内容来自于学习麻省理工学院公开课：单变量微积分-分部积分-网易公开课

开发环境准备：CSDN

二、分部积分(integration by parts)

3、换算公式（Reduction formula）

4、

5、

6、求绕 y 轴旋转，形成的体的体积，

一、多项式部分分式方法求积分

多项式相除 $\frac{P}{Q}$

1、效果

(1) 总是可以用

(2) 处理起来有些慢

2、步骤

(1) 长除法

$\frac{P(x)}{Q(x)} = quotion+\frac{R(x)}{Q(x)}, degreeR < degreeQ$

(2) 分解因式 (factor)

$\frac{R(x)}{(x+2)^4(x^2+2x+3)(x^2+4)^3}$ 这里 $deg Q =deg4+2+6 = 12, deg R(x) \le11$

(3) 建立等式（setup）

$\frac{R(x)}{(x+2)^4(x^2+2x+3)(x^2+4)^3} = \frac{A_1}{x+2}+\frac{A_2}{(x+2)^2}+\frac{A_3}{(x+2)^3}+\frac{A_4}{(x+2)^4}+$

$\frac{B_0x+C_0}{(x^2+2x+3)}+\frac{B_1x+C_1}{(x^2+4)} ＋\frac{B_2x+C_2}{(x^2+4)^2} ＋\frac{B_3x+C_3}{(x^2+4)^3}$

注意这里有12个未知数 $A_1 ....C_3$ , 要列12个等式来解决，而每个等式都会非常长，需要求助计算机。

假设这个R(x) = x+1, 那么求 $x\in(1,5)$ 的积分

import numpy as np 
from sympy import *
   
x = symbols('x')
expr = (x+1)/((x+2)**4*(x**2+2*x+3)*(x**2+4)**3)
print (float(integrate(expr, (x, 1, 5))))

1.1996123519913639e-05

对已经分开的式子求积分

a. $\int \frac{xdx}{(x^2+4)^3} = \frac{1}{4}(x^2+4)^{-2}$

b. $\int \frac{dx}{(x^2+4)^3}$

由公式： $\sqrt{a^2 +x^2} -- x = a \times tan(\theta) -- a \times sec(\theta) -- dx = asec(\theta)^2d\theta$

设 $x = tan(u) , dx = 2sec(u)^2du$

$\int \frac{dx}{(x^2+4)^3} = \int\frac{ 2sec^2(u)du}{((2sec(u))^2)^3} = \int\frac{ 2sec^2(u)du}{((4sec^2(u))^3} = \frac{1}{32}\int\frac{du}{sec^4(u)} = \frac{1}{8}\int cos^4(u)du$

由公式： $cos^2(\theta) =\frac{cos(2\theta)+1}{2}$ (半角公式)

$\frac{1}{8}\int cos^4(u)du = \frac{1}{8} \int (\frac{cos(2u)+1}{2} )^2du = \frac{1}{8} \int \frac{(cos^2(2u) + 2cos(2u)+1)du}{4}$

$= \frac{1}{32} \int (cos^2(2u) + 2cos(2u)+1)du = \frac{1}{32}(\int cos^2(2u)du + \int 2cos(2u)du + \int du)$

$= \frac{1}{32}(\int (\frac{cos(4u)+1}{2})du + sin(2u) + u) +C$

$= \frac{1}{32}(\frac{sin(4u)}{8} +\frac{u}{2} + sin(2u) + u) +C$

由公式：

$sin(2\theta) = 2sin\theta cos\theta$ (倍角公式)

$cos(2\theta) = cos^2 \theta -sin^2\theta$ (倍角公式)

$\frac{1}{32}(\frac{sin(4u)}{8} +\frac{u}{2} + sin(2u) + u) +C = \frac{1}{32}(\frac{2sin(2u)cos(2u)}{8} +\frac{u}{2} + 2sin(u)cos(u) + u) +C$

$= \frac{1}{32}(\frac{2sin(u)cos(u)(cos^2(u)-sin^2(u))}{4} +\frac{u}{2} + 2sin(u)cos(u) + u) +C$

由 $x = tan(u)$ ， $u=arctan(x) = \frac{1}{32}(\frac{sin(arctan(x))cos(arctan(x))(cos^2(arctan(x))-sin^2(arctan(x)))}{2} +\frac{arctan(x)}{2} + 2sin(arctan(x))cos(arctan(x)) + arctan(x)) +C$

expr = 1/(x**2+4)**3
print(integrate(expr,x))

(3*x**3 + 20*x)/(128*x**4 + 1024*x**2 + 2048) + 3*atan(x/2)/256

对于这个复杂度，老师是这么讲的，积分有时就是这么复杂，对谁来说都是这样，把它交给计算机去算就好，可以看到如果用计算机处理的话，就两行....

二、分部积分(integration by parts)

1、公式

由 $(uv)' = u'v + uv'$

有 $uv' = (uv)' - u'v$

有公式：

$\int uv'dx = uv - \int u'vdx$

$\int_a^b uv'dx = uv|_a^b - \int_a^b u'vdx$

2、例子

(1) $\int lnxdx$

设 $u = ln(x) , v = x$

则 $u' = \frac{1}{x} , v' = 1$

$\int uv'dx = uv + \int vu'dx \int lnxdx = \int uv'dx = uv -\int u'vdx = ln(x)x-\int\frac{xdx}{x} =ln(x)x - x+C$

$\int lnxdx = xlnx -x +C$

(2) $\int (ln(x))^2dx$

设 $u = (ln(x))^2 , v = x$

则 $u' = \frac{2ln(x)}{x} , v' = 1$

$\int (ln(x))^2dx =\int uv'dx = uv - \int u'vdx = x(ln(x))^2 - \int\frac{2ln(x)}{x}xdx = x(ln(x))^2 -\int 2ln(x)dx$

设 $u = ln(x) , v = x$

则 $u' = \frac{1}{x} , v' = 1$

$\int 2ln(x)dx = 2\int uv'dx = 2(uv - \int u'vdx) = 2(xln(x) -\int dx) = 2(xln(x) -x+c)$

$xln^2(x) -\int 2ln(x)dx = xln^2(x) - 2(xln(x) -x+c) = xln^2(x) - 2(xln(x) -x)+c$

3、换算公式（Reduction formula）

求 $\int ln^n(x)dx$

$u = ln^n(x) , u'=nln^{n-1}(x)\frac{1}{x}$

$v=x, v' =1$

$\int ln^n(x)dx = x ln^n(x) - n\int ln^{n-1}(x)dx$

总结：

$F_n(x) = \int ln^n(x)dx$

$F_{n}(x) =xln^{n}(x)-n(F_{n-1}) , (n->n-1, n-1->n-2, ....->0)$

$F_0(x) = \int ln^0(x)dx = x +C$

$F_1(x) = xln(x) - F_0(x) = xln(x) -x +C$

$F_2(x) = xln^2(x) - F_1(x) =xln^2(x) - 2(xln(x) -x )+C$

4、 $\int x^ne^xdx$

设 $v = e^x , u = x^n$

则 $v' =e^x , u' = nx^{n-1}$

$\int x^ne^xdx = \int uv'dx = uv - \int u'vdx =x^ne^x - n\int x^{n-1}e^xdx$

$F_n(x) = x^ne^x - n(F_{n-1}(x))$

$\int xe^xdx = xe^x -e^x +C$

5、 $\int x^ncos(x)dx$

设 $v = sin(x) , u = x^n$

则 $v' =cos(x) , u' = nx^{n-1}$

$\int uv'dx = uv - \int u'vdx = x^nsin(x) - n\int x^{n-1}sin(x)dx$

当n=0 $F_0(x) = sin(x) +C$

当n=1 $F_1(x) =xsin(x) - \int sin(x)dx = xsin(x) + cos(x) +C$

当n=2 $F_2(x) =x^2sin(x) - 2\int xsin(x)dx$

设 $v = -cos(x) , u = x$

则 $v' =sin(x) , u' = 1$

$\int xsin(x)dx = \int uv'dx = uv - \int u'vdx =-xcos(x) + \int cos(x)dx = -x cos(x) + sin(x) +C$

$F_2(x) =x^2sin(x) - 2\int xsin(x)dx = x^2sin(x) -2(-x cos(x) + sin(x) )+C= x^2sin(x) +2x cos(x) - 2sin(x) +C$

总结： $F_n(x) = x^nsin(x) +nF_{n-1}' - n(n-1)F_{n-2}$

检查： $F_3(x) =\int x^3cos(x)dx$

u= symbols('x')
expr1 = x**3*cos(x)
print ( 'f3 = ', integrate(expr1))

expr1 = x**4*cos(x)
print ( 'f4 = ',integrate(expr1))

x= symbols('x')
expr1 =  x**3*sin(x) + 3*x**2*cos(x) - 6*x*sin(x) - 6*cos(x) 
print('d(f3) = ', diff(expr1))

f3 = x**3*sin(x) + 3*x**2*cos(x) - 6*x*sin(x) - 6*cos(x)

f4 = x**4*sin(x) + 4*x**3*cos(x) - 12*x**2*sin(x) - 24*x*cos(x) + 24*sin(x)

d(f3) = x**3*cos(x)

这里用程序计算了 $F_3 , F_4, F_3'$ ,如上

$F_3 = x^3sin(x) +3x^2cos(x) - 6xsin(x)-6cos(x)$

$F_4 = x^4sin(x) +4x^3cos(x) -12x^2sin(x) -24xcos(x) +24sin(x)$

$F_3' = x^3cos(x)$

检查结果：符合

$F_4(x) = x^4sin(x) +4F_{3}'-12F_{2}$

$= x^4sin(x) +4F_{3}'-12F_{2} = x^4sin(x) +4(x^3cos(x))-$

$12( x^2sin(x) +2x cos(x) - 2sin(x)) +C$

$= x^4sin(x) +4x^3cos(x)-12 x^2sin(x) -24x cos(x) + 24sin(x) +C$

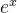6、求 $e^x$ 绕 y 轴旋转，形成的体的体积， $x\in(0,1)$

from sympy import *
import numpy as np
import matplotlib.pyplot as plt
import numpy as np
from enum import Enum
from itertools import product, combinations

from matplotlib import cm
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d.art3d import Poly3DCollection, Line3DCollection
from mpl_toolkits.mplot3d import Axes3D

fig = plt.figure(figsize=(12, 12),
                facecolor='lightyellow'
                )
# draw sphere
ax = fig.gca(fc='whitesmoke',
              projection='3d' 
           )
 
class EnumAxis(Enum):
    XAxis = 1
    YAxis = 2
    ZAxis = 3
    
def fromXYZM(xyzM):
    ret = []
    
    m=range(0,xyzM.shape[0])
    
    for b in zip(m,[0]):
        ret.append((xyzM[b]))
    for b in zip(m,[1]):
        ret.append((xyzM[b]))
    for b in zip(m,[2]):
        ret.append((xyzM[b]))
    return ret

def plot_surface(x, y, z, dx, dy, dz, ax):
    xx = np.linspace(x, x+dx, 2)
    yy = np.linspace(y, y+dy, 2)
    zz = np.linspace(z, z+dz, 2)
    
    if(dz == 0):
        xx, yy = np.meshgrid(xx, yy)
        ax.plot_surface(xx, yy, z, alpha=0.25)
    
    if(dx == 0):
        yy, zz = np.meshgrid(yy, zz)
        ax.plot_surface(x, yy, zz, alpha=0.25)
    
    if(dy == 0):
        xx, zz = np.meshgrid(xx, zz)
        ax.plot_surface(xx, y, zz, alpha=0.25)
    

def plot_opaque_cube(x, y, z, dx, dy, dz, ax):

    xx = np.linspace(x, x+dx, 2)
    yy = np.linspace(y, y+dy, 2)
    zz = np.linspace(z, z+dz, 2)

    xx, yy = np.meshgrid(xx, yy)
    ax.plot_surface(xx, yy, z)
    ax.plot_surface(xx, yy, z+dz)

    yy, zz = np.meshgrid(yy, zz)
    ax.plot_surface(x, yy, zz)
    ax.plot_surface(x+dx, yy, zz)

    xx, zz = np.meshgrid(xx, zz)
    ax.plot_surface(xx, y, zz)
    ax.plot_surface(xx, y+dy, zz)
    # ax.set_xlim3d(-dx, dx*2, 20)
    # ax.set_xlim3d(-dx, dx*2, 20)
    # ax.set_xlim3d(-dx, dx*2, 20)
    
def DrawAxis(ax, xMax, yMax, zMax):
    # 设置坐标轴标题和刻度
    ax.set(xlabel='X',
           ylabel='Y',
           zlabel='Z',
           xticks=np.arange(-xMax, xMax, 1),
           yticks=np.arange(-yMax, yMax, 1),
           zticks=np.arange(-zMax, zMax, 1)
          )

    ax.plot3D(xs=[xMax,-xMax, 0,0, 0, 0, 0,0, ],    # x 轴坐标
              ys=[0, 0,0, yMax,-yMax, 0, 0,0, ],    # y 轴坐标
              zs=[0, 0,0, 0,0, 0, zMax,-zMax ],    # z 轴坐标
              zdir='z',    # 
              c='k',    # color
              marker='o',    # 标记点符号
              mfc='r',    # marker facecolor
              mec='g',    # marker edgecolor
              ms=10,    # size
            )

def Rx(x,y,z,theta):
    A = [x,y,z] * np.matrix([[ 1, 0           , 0           ],
                   [ 0, cos(theta),-sin(theta)],
                   [ 0, sin(theta), cos(theta)]])
    return fromXYZM(A)
 
def Ry(x,y,z,theta):
    A = [x,y,z] * np.matrix([[ cos(theta), 0, sin(theta)],
                   [ 0           , 1, 0           ],
                   [-sin(theta), 0, cos(theta)]])
    return fromXYZM(A)
 
def Rz(x,y,z,theta):
    A = [x,y,z] * np.matrix([[ cos(theta), -sin(theta), 0 ],
                   [ sin(theta), cos(theta) , 0 ],
                   [ 0           , 0            , 1 ]])
    return fromXYZM(A)

def Equal(a, b, tol):
    if(abs(a - b) < tol):
        return true
    return false

def GetValuesByIdxMGrid(grid, idx):
    length = int(len(idx)/2)
    values = []
    for n in range(length):
        i = idx[2*n]
        j = idx[2*n+1]
        values.append(grid[i][j])
    return values
        
def FindIndexInMGrid(grid, value, tol):
    idx = []
    values = []
    for i in range(len(grid)):
        for j in range(len(grid[i])):
            if(Equal(grid[i][j], value, tol)):
                idx.append(i)
                idx.append(j)
                values.append(value)
                
    return idx,values
            
def MakeSliceByAxis(xarr, yarr, zarr, axis, value, tol):
    idx = []
    xret = []
    yret = []
    zret = []
    if axis == EnumAxis.XAxis:
        idx,xret = FindIndexInMGrid(xarr, value,tol)
        yret = GetValuesByIdxMGrid(yarr, idx)
        zret = GetValuesByIdxMGrid(zarr, idx)
    else:
        if axis == EnumAxis.YAxis:
            idx,yret = FindIndexInMGrid(yarr, value,tol)
            xret = GetValuesByIdxMGrid(xarr, idx)
            zret = GetValuesByIdxMGrid(zarr, idx)
        else:
            idx,zret = FindIndexInMGrid(zarr, value,tol)
            xret = GetValuesByIdxMGrid(xarr, idx)
            yret = GetValuesByIdxMGrid(yarr, idx)
            
            
    return np.array(xret),np.array(yret),np.array(zret)
    
    
def MakeRotateByAxisS(xFrom,xTo,steps,expr,thetaFrom,thetaTo,thetaSteps, rotatedBy):
    stepsArr = np.linspace(thetaFrom ,thetaTo, thetaSteps)
    xarr = []
    yarr = []
    zarr = []
    i = 0
    for theta in stepsArr:
        x,y,z = MakeRotateByAxis(xFrom,xTo,steps,expr,theta,rotatedBy)
        xarr.insert(i, x)
        yarr.insert(i, y)
        zarr.insert(i, z)
        i = i + 1
    
    return np.array(xarr), np.array(yarr), np.array(zarr)

def MakeRotateByAxis(xFrom,xTo,steps,expr,theta,rotatedBy):
    yarr = []
    xarr = np.linspace(xFrom ,xTo, steps) 
    xyz = []
    xx = []
    yy = []
    zz = []
    for xval in xarr:
        yval = expr.subs(x,xval)
        if rotatedBy == EnumAxis.XAxis:
            xyz =  Rx(xval,yval,0,theta)
        elif rotatedBy == EnumAxis.YAxis:
            xyz =  Ry(xval,yval,0,theta)
        else:
            xyz =  Rz(xval,yval,0,theta)
            
        xx.append(float(xyz[0])) #using float() to prevent isnan issue
        yy.append(float(xyz[1]))
        zz.append(float(xyz[2]))
        #if(np.isnan(float(xyz[2]))):
            #zz.append(float(0.0))
        #else:
            #zz.append(xyz[2])
    return xx,yy,zz
    
def RotateByAxis(xFrom,xTo,steps,expr,theta,color,ax,rotatedBy):
    xx,yy,zz = MakeRotateByAxis(xFrom,xTo,steps,expr,theta,rotatedBy)
    ax.plot(xx, yy, zz, color)
    
        
def GridToArray(xx,yy,zz):
    ret = []
    length = len(xx)
    n = 0
    for i in range(length):
        length1 = len(xx[i])
        for j in range(length1):
            coordinate = []
            coordinate.append(xx[i][j])
            coordinate.append(yy[i][j])
            coordinate.append(zz[i][j])
            ret.insert(n, coordinate)
            n += 1
    return np.array(ret) 
                   


DrawAxis(ax, 3,3,3)

x = symbols('x')
expr = np.e**(x)
xx,yy,zz = MakeRotateByAxisS(0,1,50,expr,0.0,2*np.pi,50, EnumAxis.YAxis)
points = GridToArray(xx,yy,zz)
ax.plot_surface(xx,yy,zz)
ax.view_init(elev=40,    # 仰角
             azim=110    # 方位角
            )
plt.show()