标题:方格分割
6x6的方格,沿着格子的边线剪开成两部分。
要求这两部分的形状完全相同。
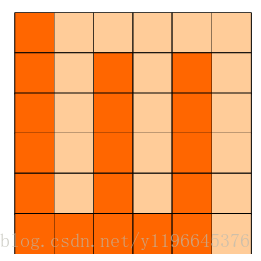
如图:p1.png, p2.png, p3.png 就是可行的分割法。
试计算:
包括这3种分法在内,一共有多少种不同的分割方法。
注意:旋转对称的属于同一种分割法。
6x6的方格,沿着格子的边线剪开成两部分。
要求这两部分的形状完全相同。
如图:p1.png, p2.png, p3.png 就是可行的分割法。
试计算:
包括这3种分法在内,一共有多少种不同的分割方法。
注意:旋转对称的属于同一种分割法。
请提交该整数,不要填写任何多余的内容或说明文字。

做法:仔细观察样例数据可以发现,要满足题目所需要求,只需要剪切的线关于图案的中点中心对称。那么我们可以将格子格子之间接壤的看作边,边与边相交的看作点。则从(3,3)点出发,找一条边到达图案的外圈,不过值得注意的是,从(3,3)出发的是看错两个人出发,两个人的线路一直是对称。所以dfs中标记的时候要一步标记两个。最后的结果要除以4,因为题目中说要旋转对称的是同一种。
#include <algorithm>
#include <string.h>
#include <iostream>
#include <stdio.h>
#include <string>
#include <vector>
#include <queue>
#include <map>
#include <set>
using namespace std;
const int N = 6;
int ans = 0;
int mpt[N+1][N+1];
int dir[4][2] = {0,1,1,0,0,-1,-1,0};
void dfs(int x,int y)
{
if(x == 0 || y == 0 || x == N || y == N){
ans ++;
return;
}
for(int i = 0 ; i < 4 ; i ++)
{
int tx = x + dir[i][0];
int ty = y + dir[i][1];
if(mpt[tx][ty])continue;
mpt[tx][ty] = 1;
mpt[N-tx][N-ty] = 1;
dfs(tx,ty);
mpt[tx][ty] = 0;
mpt[N-tx][N-ty] = 0;
}
}
int main()
{
mpt[N/2][N/2] = 1;
dfs(N/2,N/2);
printf("%d\n",ans/4);
return 0;
}
























 948
948

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








