1.函数一次求导得到的是斜率,变化率,写做:
二次求导可以得出凹凸性: ,当y''<0时,函数是凸的,开口向下,当y''>0时,函数是凹的,开口向上。
,当y''<0时,函数是凸的,开口向下,当y''>0时,函数是凹的,开口向上。
结合一阶、二阶导数可以求函数的极值。当一阶导数等于0,而二阶导数大于0时,为极小值点。
当一阶导数等于0,而二阶导数小于0时,为极大值点;当一阶导数和二阶导数都等于0时,为驻点。
2.等差数列:
第n项:![]()
公差d:![]()
![]() ,
,![]()
等比数列:
第n项,公比q:![]()
![]() ,
,![]()
等比中项:![]() ,
,![]()
3.极限中关于e:
![]()
4.渐近线:(此条转自@白水deit)
公式:
①水平渐近线:

②铅直渐近线:

举例:
求函数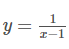
解:

即水平渐近线为 y = 0

即铅直渐近线为 x = 1
5.两个重要的极限:
6.等价无穷小的替换
当x→0,且x≠0,则
x~sinx~tanx~arcsinx~arctanx;
x~ln(1+x)~(e^x-1);
(1-cosx)~x*x/2;
[(1+x)^n-1]~nx;
loga(1+x)~x/lna;
a的x次方~xlna;
(1+x)的1/n次方~1/nx(n为正整数);
(等价替换只有在乘除之间,加减不可以,下面这个替换是错误的)









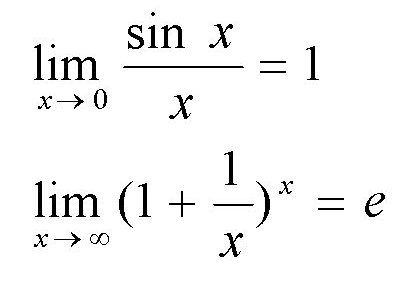

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








