2019.8.4中山纪中提高A组题解

锻造 (forging)

题目描述

Input
第一行两个整数 n, a，含义如题所示。
为了避免输入量过大，第二行五个整数 bx, by, cx, cy, p，按照下列代码
来生成 b 和 c 数组。

b[0]=by+1;c[0]=cy+1;
for(int i=1;i<n;i++){
	b[i]=((long long)b[i-1]*bx+by)%p+1;
	c[i]=((long long)c[i-1]*cx+cy)%p+1;
}

Output

输出一行一个整数，表示期望花费。

Sample Input

Sample Input1
0 6432
4602677 3944535 2618884 6368297 9477531

Sample Input2
1 3639650
6136976 5520115 2835750 9072363 9302097

Sample Input3
10 2
2 33 6 66 2333333

Sample Input4
200 5708788
0 0 0 0 1

Sample Output

Sample Output1
6432

Sample Output2
150643649

Sample Output3
976750710

Sample Output4
696441597

Data Constraint

---

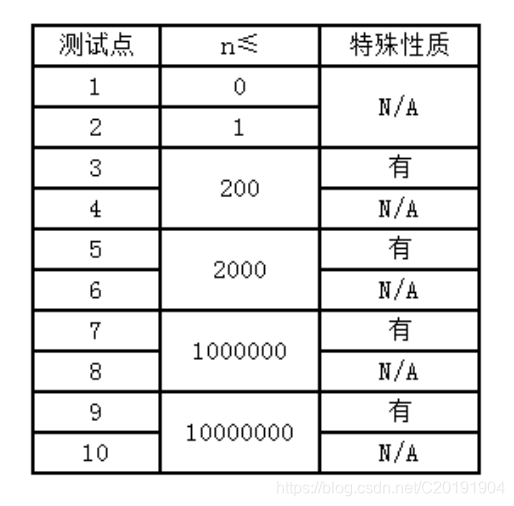
题解

不知道为什么，看到概率就会想到$Dp$…
当然这道题显然是一道$Dp$。
因为在考场上我对这道题极其有研究，所以讲得稍微详细一点。
虽然这道题很简单，但是我们从头开始（但是我太菜了）。
首先看到$n=0$，直接就是$a$嘛没什么可说的。
然后想了一下暂时还有点懵逼（开始读题读错了）。

于是考虑$n=1$。
我们先定义一下（方便表示）：$f[i]$表示得到一把$i$级剑的期望花费
显然$f[0]=a$
这里我们想到这个操作可以失败的次数是不确定的，既是我们假设我们经过$i-2$次失败后成功，既是需要$i$把$0$级剑，然后这种情况对最后答案的贡献是：
$$(1-p{)}^{i-2}\times p\times i\times f[0]$$
可以得到
$$f[1]=\sum _{i=2}^{+\infty }p\times (1-p{)}^{i-2}\times i\times f[0]$$
令$x=1-p$,即
$$f[1]=p\times f[0]\times \sum _{i=2}^{+\infty }i\times x^{i-2}$$
所以我们就是要求
$$\sum _{i=2}^{+\infty }i\times x^{i-2}$$
令$S=\sum _{i=2}^{+\infty }i\times x^{i-2}=2x^0+3x^1+4x^2+......+n{x}^{n-2}$
$$xS=2x^1+3x^2+4x^3+......+(n-1)x^{n-2}+n{x}^{n-1}$$
$$(x-1)S=n{x}^{n-1}-(x^1+x^2+......+x^{n-2})-2$$
$$(x-1)S=n{x}^{n-1}-\frac{x^{n-1}-x}{x-1}-2$$
$$S=\frac{n{x}^n-(n+1)x^{n-1}-x+2}{(x-1{)}^2}$$
因为$n\to +\infty ,0<x<1$，所以$n{x}^n\to 0,(n+1)x^{n-1}\to 0$
则$$S=\frac{2-x}{(x-1{)}^2}$$
将$p=1-x$代入$S$
则$S=\frac{1+p}{p^2}$
所以$$f[1]=f[0]\times \frac{1+p}{p}$$

于是$n=1$就处理完了，我们再看看还有什么是容易做的。
看到有$p=1$再一想，就是除了合成1级剑，其它都是一定成功。
就很容易了。
$$dp[i]=dp[i-1]+dp[i-2]$$
其中$dp[0]和dp[1]$知道。

所以我们已经有60分了，NICE
开始考虑正解。
发现每一次合成一把$i$级剑，都是要用 x { x ∈ [ 1 , + ∞ ] } x \{x\in[1,+\infty]\} x{x∈[1,+∞]}把$i-1$级剑和1把$i-2$级剑。
类比考虑合成1级剑的过程，我们得到
$$f[i]=f[i-2]+\sum _{x=1}^{+\infty }f[i-1]\times x\times (1-p{)}^{x-1}\times p$$
大家自己对照前面的过程化简一下会得到
$$f[i]=f[i-2]+\frac{f[i-1]}{p}$$
这本身也是可以理解的。
再加一个逆元就好了。
要线性筛逆元不然会T。
（线性筛逆元）

---

代码

#include<cstdio>
#include<algorithm>
using namespace std;
const int MAXN=int(1e7+5);
typedef long long LL;
#define mod 998244353
LL n,a;
LL b[MAXN];
LL c[MAXN];
LL dp[MAXN];
LL XINV[MAXN+5];
LL Pow(LL a,LL b) {
    long long ret=1,x=(long long)a,y=(long long)b;
    while(y) {
        if(y%2)
          ret=ret*x%mod;
        y/=2;
        x=(x*x)%mod;
    }
    return LL(ret)%mod;
}
LL Inv(LL a) {
    return Pow(a,mod-2);
}
void Prepare() {
    XINV[1]=1;
    for(int i=2;i<=MAXN;i++)
        XINV[i]=XINV[mod%i]*(mod-mod/i)%mod;
}
int main()
{
    Prepare();
    freopen("forging.in","r",stdin);
    freopen("forging.out","w",stdout);
    LL bx,by,cx,cy,p;
    scanf("%lld%lld",&n,&a);
    scanf("%lld%lld%lld%lld%lld",&bx,&by,&cx,&cy,&p);
    b[0]=by+1,c[0]=cy+1;
    for(LL i=1;i<n;i++) {
        b[i]=(long long)(b[i-1]*bx+by)%p+1;
        c[i]=(long long)(c[i-1]*cx+cy)%p+1;
    }
    if(n==0) {
        printf("%lld",a);
        return 0;
    }
    else if(p==1||n==1) {
        LL inv=XINV[c[0]],Min=min(c[0],b[0]);
        LL P=(LL)inv*Min%mod;
        LL ans=(LL)a*(1+P)%mod*Inv(P)%mod;
        dp[0]=a,dp[1]=ans;
        for(LL i=2;i<=n;i++)
            dp[i]=(dp[i-1]+dp[i-2])%mod;
        printf("%lld",dp[n]);
    }
    else {
        LL inv=XINV[c[0]],Min=min(c[0],b[0]);
        LL P=(LL)inv*Min%mod;
        LL ans=(LL)a*(1+P)%mod*Inv(P)%mod;
        dp[0]=a,dp[1]=ans;
        for(LL i=2;i<=n;i++) {
            LL MIN=min(c[i-1],b[i-2]);
            LL INV=XINV[MIN];
            dp[i]=((LL)dp[i-1]*c[i-1]%mod*INV%mod+dp[i-2])%mod;
        }
        printf("%lld",dp[n]);
    }
}

如果MLE就把一些LL改为int

---