生成对抗网络学习笔记4----GAN（Generative Adversarial Nets）的实现

最新推荐文章于 2024-08-12 08:56:34 发布

c2a2o2

最新推荐文章于 2024-08-12 08:56:34 发布

阅读量2.3k

点赞数

分类专栏： gans

gans 专栏收录该内容

98 篇文章 14 订阅

订阅专栏

首先是各种参考博客、链接等，表示感谢。

1、参考博客1：地址
2、参考博客2：地址

——以下，开始正文。

1、GAN的简单总结

见上一篇博客。

2、利用GAN生成1维正态分布

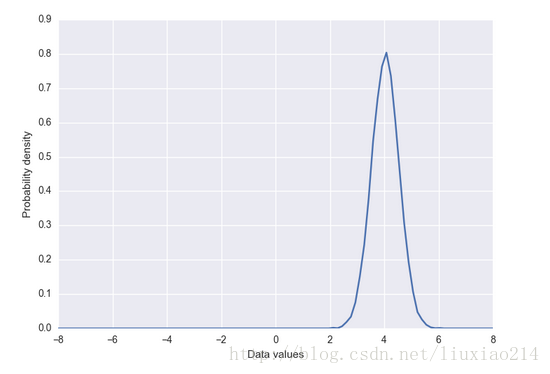
首先，我们创建“真实”数据分布，一个简单的高斯分布，均值为4，标准差为0.5,。还有一个样本函数，返回分布中给定数量的样本（按值排序过）。

class DataDistribution(object):
    def __init__(self):
        self.mu=0.4
        self.sigma=0.5

    def sample(self,N):
        samples=np.random.normal(self.mu,N)
        samples.sort()
        return samples
 
 1
2
3
4
5
6
7
8
9

我们试图学习到的数据分布大概长这样：

这里写图片描述

然后定义了一个线性运算（这里是参照后来的博客添加）：

def linear(input,output_dim,scope=None,stddev=1.0):
    norm = tf.random_normal_initializer(stddev=stddev)
    const = tf.constant_initializer(0.0)
    with tf.variable_scope(scope or 'linear'):
        w = tf.get_variable('w',[input.get_shape()[1],output_dim],initializer=norm)
        b = tf.get_variable('b',[output_dim],initializer=const)
        return tf.matmul(input,w)+b
 
 1
2
3
4
5
6
7

即简单的y=wx+b的运算，代码中使用了tf.variable_scope()，实际上这是使用了一个名为scope的变量空间，再通过tf.get_variable()定义该空间下的变量，变量的名字为“scope/w”和“scope/b”，这在很复杂的模型中有利于简化代码，并且方便用来共享变量，在后面也用到了共享变量。

我们也定义了生成器的输入噪声分布（相似的样本分布），对于生成器输入噪音采用分层抽样的方法，这些样本首先在规定的范围内均匀的生成，然后随机扰乱。

class GeneratorDistribution(object):
    def __init__(self,range):
        self.range=range

    def sample(self,N):
        return np.linspace(-self.range,self.range,N) + np.random.random(N)*0.01

 
 1
2
3
4
5
6
7

我们的生成器和判别器网络都很简单，生成器是一个通过非线性（一个softplus函数）的线性转换，接着是另一个线性转换。

def generator(input,hidden_size):
    h0=tf.nn.softplus(linear(input,hidden_size,'g0'))
    h1=linear(h0,1,'g1')
    return h1
 
 1
2
3
4

这里，我们发现，确认判别器比生产器更有力很重要，否则，它不会有足够的能力去学习而正确地判别是真实样本还是生产样本。我们设置判别网络是一个更深的神经网络，有更大的维度。它在每一层都适用tanh非线性函数，除了最后一层，最后一层使用sigmoid函数（这样我们可以将这个输出理解成可能性）。

def discriminator(input,hidden_size):
    h0=tf.tanh(linear(input,hidden_size*2,'d0'))
    h1=tf.tanh(linear(h0,hideen_size*2,'d1'))
    h2=tf.tanh(linear(h1,hidden_size*2,'d2'))
    h3=tf.sigmoid(linear(h2,1,'d2'))
    return h3
 
 1
2
3
4
5
6

接着我们可以在tensorflow graph中将这些片段拼接起来。我们对每一个网络也定义了损失函数，只是生成器的目标是欺骗判别器而已。

with tf.variable_scope('G'):
    z=tf.placeholder(tf.float32,shape=(None,1))
    G=generator(z,hidden_size)

with tf.variable_scope('D') as scope:
    x=tf.placeholder(tf.float32,shape=(None,1))
    D1=discriminator(x,hidden_size)
    scope.reuse_variables()
    D2=discriminator(G,hidden_size)

loss_d = tf.reduce_mean(-tf.log(D1)-tf.log(1-D2))
loss_g = tf.reduce_mean(-tf.log(D2))
 
 1
2
3
4
5
6
7
8
9
10
11
12

我们使用tensorflow中的GradientDescentOptimizer（学习速率指数衰减），对每一个网络都创建了一个优化器。我们也注意到，好的优化参数也需要做一些调整。

def optimizer(loss,var_list):
    initial_learning_rate = 0.005
    decay = 0.95
    num_decay_steps = 150
    batch = tf.Variable(0)
    learning_rate = tf.train.exponential_decay(
        initial_learning_rate,
        batch,
        num_deacy_steps,
        decay,
        staircases=True
    )

    optimizer = GradientDescentOptimizer(learning_rate).minimize(
        loss,
        global_step=batch,
        var_list=var_list
    )
    return optimizer

vars = tf.trainable_variables()
d_params = [v for v in vars if v.name.startswith('D/')]
g_params = [v for v in vars if v.name.startwith('G/')]

opt_d = optimizer(loss_d,d_params)
opt_g = optimizer(loos_g,g_params)
 
 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

为了训练模型，我们从数据分布和噪音分布中抽取样本，交替优化生成器和判别器的参数。

with tf.Session() as session:
    tf.initialize_all_variables().run()

    for step in xrange(num_steps):
        # update distriminator
        x = data.sample(batch_size)
        z = gen.sample(batch_size)
        session.run(
            [loss_d,opt_d],
            {
                x:np.reshape(x,(batch_size,1)),
                x:np.reshape(z,(batch_size,1))
            }
        )

        # update generator
        z = gen.sample(batch_size)
        session.run(
            [loss_g,opt_g],
            {
                z:np.reshape(z,(batch_size,1))
            }
        )
 
 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

这个动画（一个YouTube的视频）展示了在训练中，生成器是如何学习数据的近似分布。

我们可以看见，在训练过程的开始，生成器产生与真实数据非常不同的分布。最终，在收敛到集中于输入数据平均值的比较狭窄的分布之前，学习到了非常接近的分布（大约在750帧左右的时候）。

直观上这很容易理解，判别器一直在观察从真实数据和生成器中的个别样本。在这个例子中，如果生成器只是产生真实数据的平均值，它很有可能骗过判别者。

这个问题有很多的解决方法。这里我们可以添加一些early-stopping标准，当达到两个分布之间的相似阈值时，可以暂停训练。然而，并不完全清楚如何将其归纳为更大的问题，甚至在一些简单的情况下，很难保证我们的生成分布总是能达到early stopping有意义的那个点。解决这个问题一个更吸引人的办法是，给予判别器一次检验多个例子的能力。

改进：提高样本多样性

根据Tim Salimans等人最近的一篇文章，生产者折叠到一个参数设置的问题，输出是一个非常狭窄的分布这一点是GAN主要失败的模式之一。他们提出了一个解决方法：允许判别者一次观察多个样本，这项技术称之为minibatch discrimination。

在这篇文章中，minibatch discrimination被定义为，判别器有能力观察整个batch的所有样本以至于可以用来判断是来自生成器还是真实数据的任何一种方法。他们也提出一个更为特殊的方法，在同一批样本中，对于给定样本和其他样本之间的距离建模。这些距离将与原始样本结合传给判别器，因此，它可以在分类期间像样本值一样使用距离度量。

这个方法可以简单的总结如下：

利用判别器一些中间层的输出。
将它乘以一个3维tensor，来产生一个矩阵（在下面的代码中，是num_kernels * kernel_dim的大小）。
计算同一batch的所有样本的矩阵的行之间的L1-距离，并将其应用到一个负指数上。
一个样本的minibatch特征是所有指数距离的和。
使用新创建的minibatch特征连接源输入到minibatch层，并将其作为输入传给判别器的下一层。

在TensorFlow中如下：

def minibatch(input,num_kernels=5,kernel_dim=3):
    x = linear(input, num_kernels*kernel_dim)
    activation = tf.reshape(x,(-1,num_kernels,kernel_dim))
    diffs = tf.expand_dims(activation,3)-tf.expand_dims(tf.transpose(activation,[1,2,0]),0)
    abs_diffs = tf.reduce_sum(tf.abs(diffs),2)
    minibatch_features = tf.reduce_sum(tf.exp(-abs_diffs),2)
    return tf.concat(1,[input,minibatch_features])

 
 1
2
3
4
5
6
7
8

我们将实现这个minibatch判别技术，看一下是否对在我们的玩具例子上，生成器输出的折叠问题有帮助。在训练期间，生成网络新的行为如下所示：（加载不出来）

很明显，在这个例子中，在判别器中添加了minibatch后，生成器保留了大部分原始数据的宽度（尽管仍不完美）。收敛后分布如下：

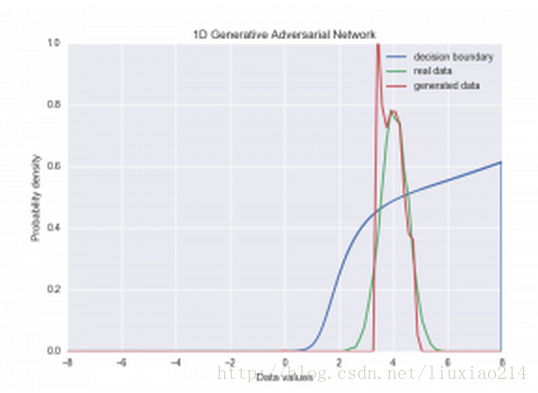
这里写图片描述

minibatch判别的最后一点是batch的大小如超参数一样重要。在我们的玩具实验中，我们使batch的保持很小（不到16左右），以训练到收敛。

在GAN类中，一共定义了以下：

初始化函数：对一些参数进行初始化。
创建模型函数：一共创建了三个模型、两个损失函数、三个模型参数集和两个优化器。
- 模型1“D_pre”：对判别模型的一个预训练，为了在开始的时候能够给生成模型有效的梯度信息以进行更新。
- 模型2“Gen”:生成模型，通过将一个噪音数据传递给一个两层感知器，输出一个具有p(g)分布的数据。
- 模型3“Disc”：判别模型，使用scope.reuse_variables()，目的是共享变量，因为真实数据和来自生成器的数据均输入到了判别器中，使用同一个变量，如果不共享，那么将会出现严重的问题，模型的输出代表着输入来自于真是数据的概率。D1是真实数据x的概率，D2是生成器生成数据g的概率。
- 损失1“loss_d”：利用公式log(D(x))+(1-log(D(G(z))))
- 损失2“loss_g”：利用公式log(D(G(z)))
- 参数集1“d_pre_params”
- 参数集2“d_params”
- 参数集3“g_params”
- 优化器1“opt_d”
- 优化器2“opt_g”
训练函数：训练过程包含了三个模型的训练，首先是对判别模型的预训练D_pre。一共1000步，预训练是利用随机数作为训练样本，随机数字代表的正态分布的值作为标签，损失函数为均方误差。然后将D_pre训练后的权重参数传给Disc，然后同时对Disc和Gen训练。
采样函数：从训练完成的模型中采样，以用来绘制图形。
画图打印等函数：利用matplotlib库和seaborn库。

最后是调用的main函数。

全部代码综合如下：

import tensorflow as tf
import numpy as np # numpy科学计算的库，可以提供矩阵运算
import matplotlib.pyplot as plt #matplotlib绘图库
from matplotlib import animation
from scipy.stats import norm #scipy数值计算库
import seaborn as sns # 数据模块可视化
import argparse #解析命令行参数和选项

sns.set(color_codes=True)  #set( )设置主题，调色板更常用
seed=42
# 设置seed，使得每次生成的随机数相同
np.random.seed(seed)
tf.set_random_seed(seed)

# define Gauss distribution of mean=4, standard deviation=0.5 
class DataDistribution(object):
    def __init__(self):
        self.mu=4
        self.sigma=0.5

    def sample(self,N):
        samples=np.random.normal(self.mu,self.sigma,N)
        samples.sort()
        return samples

class GeneratorDistribution(object):
    def __init__(self,range):
        self.range=range

    def sample(self,N):
        return np.linspace(-self.range,self.range,N) + np.random.random(N)*0.01

def linear(input,output_dim,scope=None,stddev=1.0):#线性计算，计算y=wx+b
    norm = tf.random_normal_initializer(stddev=stddev)
    const = tf.constant_initializer(0.0)
    with tf.variable_scope(scope or 'linear'):
        w = tf.get_variable('w',[input.get_shape()[1],output_dim],initializer=norm)
        b = tf.get_variable('b',[output_dim],initializer=const)
        return tf.matmul(input,w)+b

def generator(input,hidden_size):
    h0=tf.nn.softplus(linear(input,hidden_size,'g0'))
    h1=linear(h0,1,'g1')
    return h1

def discriminator(input,hidden_size,minibatch_layer=True):
    h0=tf.tanh(linear(input,hidden_size*2,'d0'))
    h1=tf.tanh(linear(h0,hidden_size*2,'d1'))
    if minibatch_layer:
        h2=minibatch(h1)
    else:
        h2=tf.tanh(linear(h1,hidden_size*2,scope='d2'))
    h3=tf.sigmoid(linear(h2,1,scope='d3'))
    return h3

def minibatch(input,num_kernels=5,kernel_dim=3):
    x = linear(input, num_kernels*kernel_dim,scope='minibatch',stddev=0.02)
    activation = tf.reshape(x,(-1,num_kernels,kernel_dim))
    diffs = tf.expand_dims(activation,3)-tf.expand_dims(tf.transpose(activation,[1,2,0]),0)
    abs_diffs = tf.reduce_sum(tf.abs(diffs),2)
    minibatch_features = tf.reduce_sum(tf.exp(-abs_diffs),2)
    return tf.concat([input,minibatch_features],1)

def optimizer(loss,var_list,initial_learning_rate):
    initial_learning_rate = 0.005
    decay = 0.95
    num_decay_steps = 150
    batch = tf.Variable(0)
    learning_rate = tf.train.exponential_decay(
        initial_learning_rate,
        batch,
        num_decay_steps,
        decay,
        staircase=True
    )

    optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(
        loss,
        global_step=batch,
        var_list=var_list
    )
    return optimizer

class GAN(object):
    def __init__(self,data,gen,num_steps,batch_size,minibatch,log_every,anim_path):
        self.data = data
        self.gen = gen
        self.num_steps = num_steps
        self.batch_size = batch_size
        self.minibatch = minibatch
        self.log_every = log_every
        self.mlp_hidden_size = 4
        self.anim_path = anim_path
        self.anim_frames =[]

        # can use a higher learning rate when not using the minibatch layer
        if self.minibatch:
            self.learning_rate = 0.005
        else:
            self.learning_rate = 0.03

        self._create_model()

    def _create_model(self):
        # in order to make sure that the discriminator is providing useful gradient information
        # to the generator from the start, we're going to pretrain the discriminator using a maximum
        # likelihood objective. we define the network for this pretraining step scoped as D_pre.
        with tf.variable_scope('D_pre'):
            self.pre_input = tf.placeholder(tf.float32, shape=(self.batch_size,1))
            self.pre_labels = tf.placeholder(tf.float32, shape=(self.batch_size,1))
            D_pre = discriminator(self.pre_input, self.mlp_hidden_size,self.minibatch)
            self.pre_loss = tf.reduce_mean(tf.square(D_pre-self.pre_labels))
            self.pre_opt = optimizer(self.pre_loss,None,self.learning_rate)

        # this defines the generators network: it takes samples from a noise distribution
        # as input, and passes them through an MLP
        with tf.variable_scope('Gen'):
            self.z = tf.placeholder(tf.float32,shape=(self.batch_size,1))
            self.G = generator(self.z,self.mlp_hidden_size)

        # this discriminator tries to tell the difference between samples from the true data distribution
        # (self.x) and the generated samples (self.z)
        with tf.variable_scope('Disc') as scope:
            self.x = tf.placeholder(tf.float32,shape=(self.batch_size,1))
            self.D1 = discriminator(self.x,self.mlp_hidden_size,self.minibatch)
            scope.reuse_variables()
            self.D2 = discriminator(self.G,self.mlp_hidden_size,self.minibatch)

        # define the loss for discriminator and generator network
        # and create optimizer for both
        self.loss_d = tf.reduce_mean(-tf.log(self.D1)-tf.log(1-self.D2))
        self.loss_g = tf.reduce_mean(-tf.log(self.D2))

        self.d_pre_params = tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES,scope='D_pre')
        self.d_params = tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES,scope='Disc')
        self.g_params = tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES,scope='Gen')

        self.opt_d = optimizer(self.loss_d,self.d_params,self.learning_rate)
        self.opt_g = optimizer(self.loss_g,self.g_params,self.learning_rate)

    def train(self):
        with tf.Session() as session:
            tf.global_variables_initializer().run()

            # pretraining discriminator
            num_pretrain_steps = 1000
            for step in xrange(num_pretrain_steps):
                d = (np.random.random(self.batch_size)-0.5)*10.0
                labels = norm.pdf(d,loc=self.data.mu,scale=self.data.sigma)
                pretrain_loss,_ = session.run(
                    [self.pre_loss,self.pre_opt],
                    {
                        self.pre_input: np.reshape(d,(self.batch_size,1)),
                        self.pre_labels: np.reshape(labels,(self.batch_size,1))
                    }
                    )
            self.weightsD = session.run(self.d_pre_params)

            # copy weights from pre-training over to new D network
            for i,v in enumerate(self.d_params):
                session.run(v.assign(self.weightsD[i]))

            for step in xrange(self.num_steps):
                # update distriminator
                x = self.data.sample(self.batch_size)
                z = self.gen.sample(self.batch_size)
                loss_d,_=session.run(
                    [self.loss_d,self.opt_d],
                    {
                        self.x:np.reshape(x,(self.batch_size,1)),
                        self.z:np.reshape(z,(self.batch_size,1))
                    }
                )

                # update generator
                z = self.gen.sample(self.batch_size)
                loss_g,_=session.run(
                    [self.loss_g,self.opt_g],
                    {
                        self.z:np.reshape(z,(self.batch_size,1))
                    }
                )

                if step % self.log_every == 0:
                    print('{}:{}\t{}'.format(step,loss_d,loss_g))
                if self.anim_path:
                    self.anim_frames.append(self._samples(session))

            if self.anim_path:
                self._save_animation()
            else:
                self._plot_distributions(session)

    def _samples(self,session,num_points=10000,num_bins=100):
        # return a tuple (db,pd,pg), where db is the current decision boundary
        # pd is a histogram of samples from the data distribution,
        # and pf is a histogram of generated samples.
        xs = np.linspace(-self.gen.range,self.gen.range,num_points)
        bins = np.linspace(-self.gen.range,self.gen.range,num_bins)

        # decision boundary
        db = np.zeros((num_points,1))
        for i in range(num_points // self.batch_size):
            db[self.batch_size * i :self.batch_size * (i+1)] = session.run(
                self.D1,
                {
                    self.x:np.reshape(
                      xs[self.batch_size * i :self.batch_size * (i+1)],
                      (self.batch_size,1)
                    )
                }
            )
        # data distribution
        d = self.data.sample(num_points)
        pd,_ = np.histogram(d,bins=bins,density=True)

        # generated samples
        zs = np.linspace(-self.gen.range,self.gen.range,num_points)
        g = np.zeros((num_points,1))
        for i in range(num_points // self.batch_size):
            g[self.batch_size * i :self.batch_size * (i+1)] = session.run(
                self.G,
                {
                    self.z:np.reshape(
                        zs[self.batch_size * i : self.batch_size * (i+1)],
                        (self.batch_size,1)
                    )
                }
            )
        pg,_=np.histogram(g,bins=bins,density=True)

        return db,pd,pg

    def _plot_distributions(self,session):
        db,pd,pg = self._samples(session)
        db_x = np.linspace(-self.gen.range,self.gen.range,len(db))
        p_x = np.linspace(-self.gen.range,self.gen.range,len(pd))
        f,ax = plt.subplots(1)
        ax.plot(db_x,db,label='decision boundary')
        ax.set_ylim(0,1)
        plt.plot(p_x,pd,label='real data')
        plt.plot(p_x,pg,label='generated data')
        plt.title('1D Generative Adversarial Network')
        plt.xlabel('Data values')
        plt.ylabel('Probability density')
        plt.legend()
        plt.show()

    def _save_animation(self):
        f,ax = plt.subplots(figsize=(6,4))
        f.suptitle('1D Generative Adversarial Network',fontsize=15)
        plt.xlabel('Data values')
        plt.ylabel('Probability density')
        ax.set_xlim(-6,6)
        ax.set_ylim(0,1.4)
        line_db, = ax.plot([],[],label='decision boundary')
        line_pd, = ax.plot([],[],label='real data')
        line_pg, = ax.plot([],[],label='generated data')
        frame_number = ax.text(
            0.02,
            0.95,
            '',
            horizontalalignment='left',
            verticalalignment='top',
            transform=ax.transAxes
        )
        ax.legend()

        db,pd,_ = self.anim_frames[0]
        db_x = np.linspace(-self.gen.range,self.gen.range,len(db))
        p_x = np.linspace(-self.gen.range,self.gen.range,len(pd))

        def init():
            line_db.set_data([],[])
            line_pd.set_data([],[])
            line_pg.set_data([],[])
            frame_number.set_text('')
            return (line_db,line_pd,line_pg,frame_number)

        def animate(i):
            frame_number.set_text(
                'Frame: {}/{}'.format(i,len(self.anim_frames))
            )
            db,pd,pg = self.anim_frames[i]
            line_db.set_data(db_x,db)
            line_pd.set_data(p_x,pd)
            line_pg.set_data(p_x,pg)
            return (line_db,line_pd,line_pg,frame_number)

        anim = animation.FuncAnimation(
            f,
            animate,
            init_func=init,
            frames=len(self.anim_frames),
            blit=True
        )
        anim.save(self.anim_path,fps=30,extra_args=['-vcodec','libx264'])

def main(args):
    model = GAN(
        DataDistribution(),
        GeneratorDistribution(range=8),
        args.num_steps,
        args.batch_size,
        args.minibatch,
        args.log_every,
        args.anim
    )
    model.train()

def parse_args():
    parser = argparse.ArgumentParser()
    parser.add_argument('--num-steps',type=int,default=1200,
                        help='the number of training steps to take')
    parser.add_argument('--batch-size',type=int,default=12,
                        help='the batch size')
    parser.add_argument('--minibatch',type=bool,default=False,
                        help='use minibatch discrimination')
    parser.add_argument('--log-every',type=int,default=10,
                        help='print loss after this many steps')
    parser.add_argument('-anim',type=str,default=None,
                        help='the name of the output animation file (default: none)')
    return parser.parse_args()

if __name__ == '__main__':
    main(parse_args())

 
 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327

运行有两种模式，一是默认，二是使用minibatch。命令如下：

$ python gan.py
$ python gan.py --minibatch True
 
 1
2

运行结果如下：

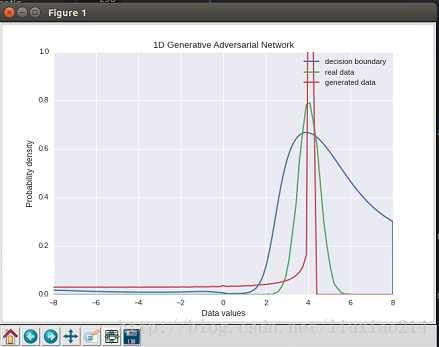
这里写图片描述

其中，绿色代表真实数据，红色代表生成数据，蓝色代表判别为真实数据的概率，可以看到高于50%，效果不是很好，而且虽然生成数据很接近真实数据，但是其分布过于狭窄。这是因为判别器只能对单一的数据进行处理，不能很好的反映数据集的分布情况。所以可以采用minibatch。

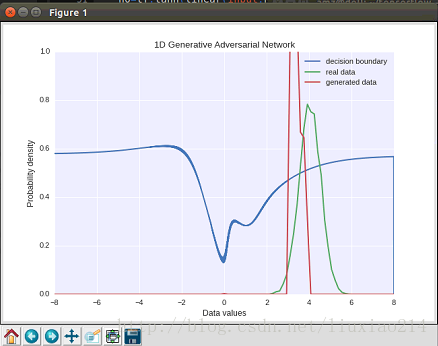
这里写图片描述

感觉分布还是不是特别好，好像没有变宽很多，但是真实数据的概率大约变为50%左右了。

c2a2o2

关注

0
点赞
踩
5

收藏

觉得还不错? 一键收藏
0
评论
复制链接

分享到 QQ

分享到新浪微博

扫一扫

专栏目录