#排序
排序是我们程序中经常面对的问题,那么排序的严格定义是什么呢?
假设含有n个记录的序列为{r1,r2,r3…..,rn},其对应的关键字分别为{k1,k2,k3…..,kn},需确定1,2,…..,n的一种排列p1,p2,……..,pn,使其相应的关键字满足Kp1<=Kp2…….<=Kp2(非递减或非递增)关系,即使得序列成为一个按关键字有序的序列{rp1,rp2……rpn},这样的操作就称为排序。
内排序和外排序
根据在排序过程中待排序的记录是否全部被放置在内存中,将其分为:内排序和外排序。
内排序是在排序的整个过程中,待排序的所有记录全部被放置在内存中,外排序是由于需要排序的记录太多,不能同时放置咋子内存中,整个排序过程需要在内外存之间多次交换数据才能进行,
对于内排序来说,排序算法的性能主要受以下3个方面影响:
(1)时间性能,排序是数据处理中经常执行的操作,因此排序算法的时间性能是衡量其好坏的最重要的标志,内排序中主要进行比较和移动这两种操作。高效率的算法应该尽可能少的进行比较和移动。
(2)辅助空间,指的是除了存放待排序数据所占用的存储空间外,执行算法所需要的其他存储空间。
(3)算法的复杂性。
冒泡排序
冒泡排序(Bubble Sort)是一种交换排序,基本思想是两两比较相邻的元素,如果他们的顺序错误就把他们交换过来,直到排序完成。这个算法的名字由来是因为越大的元素会经由交换慢慢“浮”到数列的顶端
冒泡排序算法的过程如下:
(1)比较相邻的元素。如果第一个比第二个大,就交换他们两个。
(2)对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。在这一点,最后的元素应该会是最大的数。
(3)针对所有的元素重复以上的步骤,除了最后一个。
(4)持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
简单实现
void sort(int[] a) {
for(int i=0;i<a.length;i++) {
for(int j=0;j<a.length-i-1;j++) {
if(a[j]>a[j+1]) {
int temp=a[j];
a[j]=a[j+1];
a[j+1]=temp;
}
}
}
}这应该是最简单的排序代码了,不过这个代码效率是非常低下的,所以我们需要进行改进。
冒泡排序优化
试想一下,有这么一个数组{2,1,3,4,5,6,7,8},也就是说,除了第一和第二个元素需要交换,其他的已经是正常的顺序了 ,如果我们用上面的算法,毫无疑问它会将每个循环再执行一次,这就耗费了大量的时间,所以我们可以设置一个标志位,当没有任何数据交换时说明已经有序,不需要进行后面的循环操作。
void bestsort(int[] a) {
boolean flag=true;
for(int i=0;i<a.length&&flag;i++) {
flag=false;
for(int j=0;j<a.length-i-1;j++) {
if(a[j]>a[j+1]) {
int temp=a[j];
a[j]=a[j+1];
a[j+1]=temp;
flag=true;
}
}
}
}冒泡排序时间复杂度分析
当最好的情况,也就是排序的数组本身是有序的,那么我们需要比较一轮,也就是n-1次,没有数据交换时间复杂度为O(n),最坏的情况,也就是排序的数组为逆序时,此时需要比较n-1+n-2+……2+1次,也就是n(n-1)/2,并且还需要移动,此时时间复杂度为O(n^2).这时候我们就知道了冒泡排序是一种效率多么低下的算法,尽管有很多人对它进行各种各样的优化,但是排序的特性在这里,性能依然大大相差于其他算法。
选择排序
选择排序的思想是每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完。
简单选择排序
public static void selectsort(int[] arr) {
for (int i=0;i<arr.length;i++) {
int minindex=i;
for(int j=i+1;j<arr.length;j++) {
if(arr[minindex]>arr[j]) {
minindex=j;
}
}
if(i!=minindex) {
int temp=arr[i];
arr[i]=arr[minindex];
arr[minindex]=temp;
}
}
} 简单选择排序时间复杂度分析
从算法上来看,选择排序交换移动次数相当少,分析时间复杂度,无论是最好还是最坏情况,比较次数都是一样的多,为n(n-1)/2次,而交换次数最好情况为0,最坏情况逆序为n-1次,因此总的来看,选择排序的时间复杂度为O(n^2),虽然说和冒泡排序同为O(n^2),但是选择排序的性能还是要优于冒泡排序。
插入排序
插入排序的思想是将一个记录插入到已经排好序的有序表中,从而得到一个新的、记录数加一的有序表。
void insertSort(int[] arr) {
for(int i=1;i<arr.length;i++) {
for(int j=i;j>0;j--) {
if(arr[j]<arr[j-1]) {
int temp=arr[j];
arr[j]=arr[j-1];
arr[j-1]=temp;
}else{
break;
}
}
}
}插入排序时间复杂度分析
当最好的情况,也就是要排序的表本身就有序时,那么只需要比较n-1次,此时时间复杂度为O(n),当最坏情况发生时,即待排序的数组为逆序,此时需要比较1+2+3+。。。(n-1)次,时间复杂度为O(n^2),但是同样为O(n^2),插入排序的性能要比冒泡和选择排序性能要好。
希尔排序
希尔排序是D.L.Shell发明的一种排序算法,在这之前的排序算法的时间复杂度基本都是O(n^2),希尔排序是突破这个时间复杂度的第一批算法之一,也被称为缩减增量排序。
基本思想是先将整个待排序的记录序列分割成为若干子序列(由相隔某个“增量”的元素组成)分别进行直接插入排序,然后依次缩减增量再进行排序,待整个序列中的记录“基本有序”时,再对全体记录进行依次直接插入排序。所谓的基本有序,就是小的关键字基本在前面,大的基本在后面,例如{2,1,3,6,4,7,5,8,9}就可以称为基本有序,但{1,5,9,3,7,8,2,4,6}这样的9在第三位,2很靠后,就谈不上基本有序。
我们来举一个例子来更好的理解一下希尔排序。
(1)我们有一个数组为{49,38,65,97,26,13,27,49,55,4},长度为10,我们设增量为数组长度/2,所以这里增量为5
(2) 然后按照增量将整个元素序列分为子序列,这里分为{49,13},{38,27},{65,49},{97,55},{26,4},然后对其进行直接排序为{13,49},{27,38},{49,65},{55,97},{4,26},第一次排序后即为13 ,27, 49 ,55 , 4, 49,38,65,97 ,26
(3)然后我们缩减增量,缩减规律为当前增量/2,即5/2=2,然后再分为子序列{13,49,4,38,97},{27,55,49,65,26},然后继续直接插入排序,以此类推
(4)当增量缩减到0时,则排序完成得到数组。
代码实现
void shellSort(int[] arr) {
//确定增量,这里使用(数组长度/2),并且每次/2
for(int gap=arr.length/2;gap>0;gap/=2) {
//分组进行交换
for(int i=gap;i<arr.length;i++) {
for(int j=i-gap;j>=0&&arr[j]>arr[j+gap];j-=gap) {
int temp=arr[j];
arr[j]=arr[j+gap];
arr[j+gap]=temp;
}
}
}
}通过我们的分析,大家应该明白,希尔排序的关键就是增量,将相隔某个增量的数据组成一个子序列,形成跳跃式的移动,使得移动次数变少,效率变高。这里的增量的选取非常关键,可究竟选取什么增量才是最好?目前还是一个数学难题,到现在位置还没有找到一种最好的增量,不过大量的研究表明,当增量为 dlta[k]=2^(t-k+1)-1(0<=k<=t<=[log2(n+1)])时,可以有很不错的效率,时间复杂度为O(n^(3/2)),效率相比前面几种有了大大的提高,不过因为是跳跃式移动,希尔排序并不是一种稳定的排序算法。
堆排序
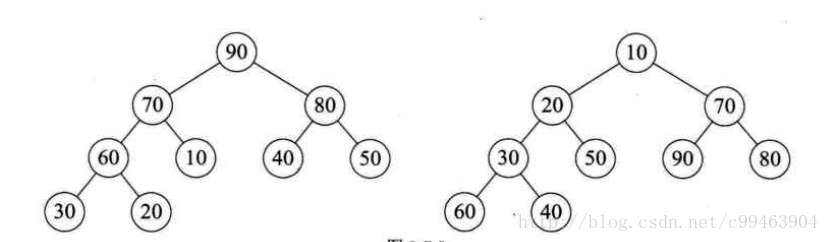
我们先来了解一下堆这种数据结构,堆是具有下列性质的完全二叉树:每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆;每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆。下图左为大顶堆,右为小顶堆
如果给结点按照层序遍历方式编号,则结点之间满足如下关系
堆排序就是利用堆进行排序的方法。基本思想是,将待排序的序列构造成一个大顶堆(或小顶堆),此时整个序列的最大值就是根结点,将其移除输出,然后将剩下的元素再构成一个大顶堆,继续输出最大的元素,反复执行,便能得到一个有序序列。
这里我们就需要解决两个最关键的问题
- 1.如何将n个待排序元素构建成堆?
- 2.输出堆顶元素后,如何调整剩余元素使其成为一个新的堆?
我们先来看第一个问题,我们曾经学习过一个结论,对于完全二叉树而言,第n个元素的双亲节点是n/2,也就是说最后一个结点n是n/2的子树,然后我们就从n/2结点开始排序,使其子树成为堆,然后从n/2以此向前对每一个有子树的根结点进行排序,使其成为堆,直到根结点。
然后我们来看第二个问题,如果有n个元素的堆,输出堆顶元素后,我们将堆底元素放在堆顶,然后再与其左右子树进行比较交换构建堆,这样到比较完排序过程也就完成了。
代码实现
public class HeapSort {
public static void main(String[] args) {
int[] sort = new int[] { 1, 0, 10, 20, 3, 5, 6, 4, 9, 8, 12, 17, 34, 11 };
heapSort(sort);
for(int i:sort) {
System.out.print(i+" ");
}
}
//堆排序
private static void heapSort(int[] data) {
//先将当前数组转换为最大堆
buildMaxHeapify(data);
// 末尾与头交换,然后将剩下的元素构建最大堆
for (int i = data.length - 1; i > 0; i--) {
int temp = data[0];
data[0] = data[i];
data[i] = temp;
maxHeapify(data, i, 0);
}
}
//构建最大堆
private static void buildMaxHeapify(int[] data) {
//从最后一个具有子树的结点开始构建
for (int i = data.length/2; i >= 0; i--) {
maxHeapify(data, data.length, i);
}
}
/**
*创建最大堆
* data为数组,heapsize为数组大小,index为当前根结点
**/
private static void maxHeapify(int[] data, int heapSize, int index) {
// 获取当前结点的左右孩子结点
int left =index*2;
int right = index*2+1;
//与左右结点判断,获取最大的
int largest = index;
if (left < heapSize && data[index] < data[left]) {
largest = left;
}
if (right < heapSize && data[largest] < data[right]) {
largest = right;
}
// 得到最大值后可能需要交换,如果交换了,其子节点可能就不是最大堆了,所以还需要递归调整其子结点
if (largest != index) {
int temp = data[index];
data[index] = data[largest];
data[largest] = temp;
maxHeapify(data, heapSize, largest);
}
}
}堆排序的运行时间主要用在初始化构建堆和重建堆的反复筛选上,堆排序的时间复杂度为O(nlogn),这在性能上显然要远远好于冒泡、简单选择、直接插入的O(n^2)的时间复杂度。有兴趣的可以去看一下堆排序的数学计算时间复杂度的过程
归并排序
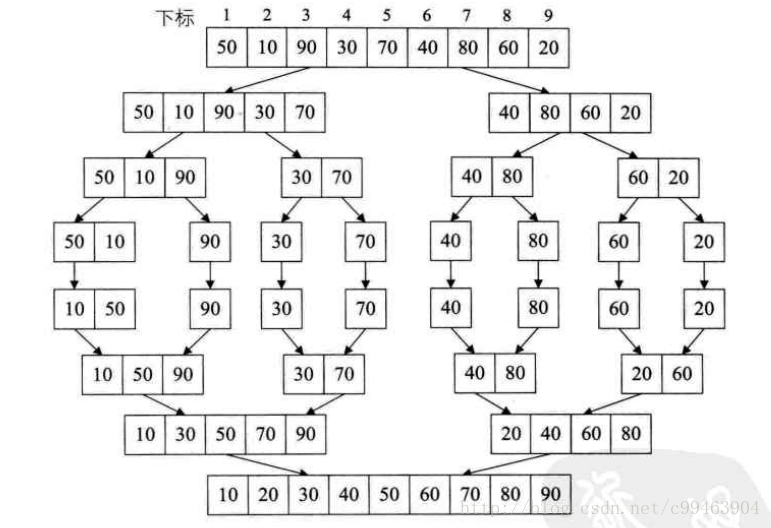
归并排序就是利用归并的思想实现排序。基本思想是假设初始序列有n个记录,可以将其看成n个子序列,然后两两归并,得到n/2个有序子序列,然后继续两两归并,直到最后得到一个长度为n的有序序列。这种排序方法称为2路归并排序。
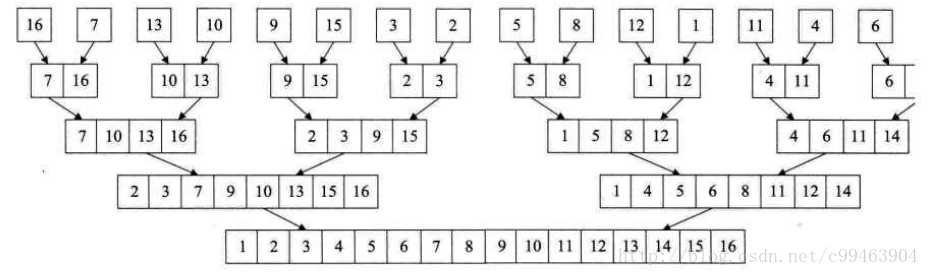
对于给定一个无序的数组,我们需要先将其拆分为一个个有序子序列,然后再进行合并。
我们先来看看如何将两个有序序列进行合并,这个非常简单,只要以此比较两个序列中的数,谁小就取谁,如果有一个序列空了,那么就依次把剩下序列中数放入即可。那么如何使一个无序序列分解为有序子序列呢,我们可以将当前序列不断的进行分解,当分出来的子序列只有一个数据时,可以认为这个子序列已经达到了有序,然后再合并相邻的二个子序列就可以了
代码实现
public class MergeSort {
public static void main(String[] args) {
int []array= {9,8,7,6,5,4,23,2,1,0};
mergeSort(array);
for (int i = 0; i < array.length; ++i) {
System.out.print(array[i] + " ");
}
}
public static void mergeSort(int[] array) {
//创建一个辅助数组来方便我们进行合并
int[] temp=new int[array.length];
//将整个数组分解
mergesort(array,0,array.length-1,temp);
}
//将整个无序数组分解为一个个的单元素,然后合并,参数为无序数组、数组的起始位置、数组的结束位置、辅助数组
static void mergesort(int a[], int first, int last, int temp[])
{
//如果起始位置小于结束位置,说明未完全分解,则继续递归
if (first < last)
{
//获取中间位置,进行分解
int mid = (first + last) / 2;
//对左边数组进行分解
mergesort(a, first, mid, temp);
//对右边数组进行分解
mergesort(a, mid + 1, last, temp);
//分解完毕后,进行合并
mergearray(a, first, mid+1, last, temp); //再将二个有序数列合并
}
}
//firstindex为第一个数组起始位置,secondindex为第二个数组起始位置,last为第二个数组结束位置
static void mergearray(int a[], int firstindex, int secondindex, int last, int temp[])
{
//获取第一个数组的结束位置
int firstend=secondindex-1;
int tmppos=firstindex;
//获取当前合并的元素个数
int numbers=last-firstindex+1;
//进行比较
while (firstindex <= firstend && secondindex <= last)
{
if (a[firstindex] <= a[secondindex])
temp[tmppos++] = a[firstindex++];
else
temp[tmppos++] = a[secondindex++];
}
//如果某个数组为空了,则将另一个数组剩下的元素依次放入数组
while (firstindex <= firstend)
temp[tmppos++] = a[firstindex++];
while (secondindex <= last)
temp[tmppos++] = a[secondindex++];
//将我们的辅助数组复制到原数组中,要从后向前复制
for (int i = 0; i < numbers; i++,last--)
a[last] = temp[last];
}
}归并排序时间复杂度分析
归并排序的时间复杂度为O(nlogn),因为归并排序每次都是在相邻的数据中进行操作,所以归并排序在O(N*logN)的几种排序方法(快速排序,归并排序,希尔排序,堆排序)也是效率比较高的。
快速排序
快速排序的基本思想是:选择一个基准元素(称为枢纽元),通过一趟排序将待排记录分割成独立的两部分,其中一部分记录的关键字均比基准元素小,另一部分元素都比基准元素大,这时候枢纽元元素的位置就已经确定了,然后再分别对这两部分记录继续进行排序,直到左右两部分只有一个数时结束,以达到整个序列有序的目的。
public class QuickSort {
public static void main(String[] args) {
int [] arr= {74,200,200,74,57,1023,1,85,32,57,99};
//调用快速排序
quickSort(arr);
for(int a:arr) {
System.out.print(a+" ");
}
}
public static void quickSort(int[] array) {
quickSort(array,0,array.length-1);
}
public static void quickSort(int[] array,int low,int high) {
int pivot;
if(low<high) {
//得到枢纽元的位置,这时候枢纽元已经固定了在数组中的位置
pivot=partition(array,low,high);
//对左侧子序列进行快排
quickSort(array,low,pivot-1);
//对右侧子序列进行快排
quickSort(array,pivot+1,high);
}
}
//选取枢纽元,然后把它放入固定的位置,使其左侧元素都小于它,右侧元素都大于它
public static int partition(int[] array,int low, int high) {
//选取第一个元素为枢纽元
int pivotkey=array[low];
while(low<high) {
//当右边元素小于枢纽元时跳出循环,与左边元素交换位置
while(low<high&&array[high]>=pivotkey) {
high--;
}
swap(array,low,high);
//当左边元素大于枢纽元时跳出循环,与右边元素交换位置
while(low<high&&array[low]<=pivotkey) {
low++;
}
swap(array,low,high);
}
//返回当前枢纽元确定的位置
return low;
}
public static void swap(int[] array,int low,int high) {
int temp=array[low];
array[low]=array[high];
array[high]=temp;
}
}枢纽元优化
我们前面的枢纽元直接选取了第一个元素,这是一种非常蠢的做法,如果我们的数组是反序的,那么就会产生一个特别差的分割效果,所有元素都被分割到一侧,时间效率是二次的,极其差劲,所以我们需要改变一下。有人提出了一种方法就是随机选取枢纽元,但是也不是最好的选择,因为随机数生成也花费不少的时间性能。于是就有了我们要使用的三数取中法。
三数取中法即取三个关键字先进行排序,将中间数作为枢纽元。一般是选左端、右端和中间三个数。这样这个中间数一定不会是最小或者最大的数。
我们只需要在取枢纽元的前面加上如下代码
public static int partition(int[] array,int low, int high) {
//交换之后,array[low]位置上就是我们的中间值
int pivotkey;
int mid=low+(high-low)/2;
if(array[low]>array[high]) {
swap(array,low,high);
}
if(array[mid]>array[high] ) {
swap(array,high,mid);
}
if(array[mid]>array[low] ) {
swap(array,mid,low);
}
pivotkey=array[low];
while(low<high) {
while(low<high&&array[high]>=pivotkey) {
high--;
}
swap(array,low,high);
while(low<high&&array[low]<=pivotkey) {
low++;
}
swap(array,low,high);
}
return low;
}小数组优化
对于很小的数组,快速排序的效率是不如插入排序的。所以我们增加一个判断,当high-low不大于某个常数,有研究说是7比较合适,就使用插入排序。
public static void quickSort(int[] array,int low,int high) {
if(high-low>7) {
int pivot;
pivot=partition(array,low,high);
quickSort(array,low,pivot-1);
quickSort(array,pivot+1,high);
}else {
InsertSort.insertSort(array);
}
}
当然快速排序还有很多种的更加细致的优化,有兴趣可以去了解一下。










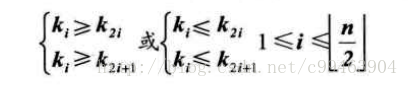















 1073
1073

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








